聚类分析
Table of Contents
- 1. 聚类分析的内容和方法
- 2. 距离和相似度
- 3. 聚类分析实现(using R)
- 4. 聚类分析实现(Using Matlab)
1 聚类分析的内容和方法
- 聚类分析的背景
- 聚类分析也称为群分析, 是研究对样品或指标进行分类的一种多元统计方法
- 在实际问题中, 经常遇到分类问题,
- 大气污染的轻重区域,
- 在经济学中, 根据人均国 民收入, 人均工农业产值, 人均消费水平等多种指标对各个国家的经济发展状况进 行分类等,
- 个人进行股市投资时, 会有选择性的把股市上的股票分为几种, 潜力股, 垃 圾股等,
- 聚类分析和判别分析之间的关系: 判别分析是已知类别及性质, 对新样本进行归类, 而聚类 分析是对待分析的数据不知道该分为几类, 需要从样本数据出发进行分析
- 在机器学习, 聚类分析属于无指导的机器学习
- 聚类分析的内容十分丰富, 按照聚类方法有如下几种
- 系统聚类法:开始每个对象自成一类, 然后每次将最近似的两类进行, 合并后重新 计算新类与其他类之间的距离或相似程度, 一直持续进行到所有对象合并为一类
- 可以通过一张谱系图进行描述聚类的过程
- 模糊聚类法:利用模糊集理论来处理分类问题, 对经济领域中具有模糊特征的两态数据或 多态数据具有较好的分类效果
- 最优分割法, 调优法(动态聚类法), 图论聚类法等方法
- 聚类分析分类对象
- 聚类分析按照分类对象不同分为两类
- 变量聚类:可以了解变量间及变量组合间的亲疏关系根据分类结果及他们之间的关系, 在每一类中选择有代表性的变量
- 样品聚类对样品进行分类, 分类的结果是直观的, 且比传统方法更细致, 全面, 但是对 任何观测数据 都没有唯一“正确的”分类方法
- 本课程重点是 系统聚类法, 且主要讨论样品聚类问题
2 距离和相似度
- 原始样本数据
- 设有n个样本, 每个样本测得m个指标, 得观测数据为 xij,i=1,⋯,n,j=1,⋯,m
- 计算第j个指标的均值和标准差, 极差
- x¯j=1n∑i=1nxij
- sj=1n−1∑i=1n(xij−x¯j)2−−−−−−−−−−−−−−−−√, j=1,⋯,m
- Rj=max(xij,i=1,⋯,n)−min(xij,i=1,⋯,n)
- 数据预处理–数据变换
- 数据在进行聚类之前因为量纲不同, 将影响样品间的距离计算和类间距离的计算, 需 要进行适当的变换
- 中心化变换 (对每个变量) x∗ij=xij−x¯j ,变换后数据的均值为0, 协方差阵不变
S∗=(sij), sij=1n−1∑t=1n(xti−x¯i)(xtj−x¯j)=1n−1∑t=1nx∗tix∗tj
- 标准化变换
x∗ij=xij−x¯jsj,i=1,⋯,n,j=1,⋯,m
变换后的数据, 均值为0, 标准差为1, 也称为 Zcore 变换
- 极差变换
- 极差标准化变换
x∗ij=xij−x¯jRj
变换后的数据, 每个变量的样本均值为0, 极差为1, 且 |x∗ij|<1
- 极差正规化变换
x∗ij=xij−min1≤t≤nxtjRj
变换之后的数据 0≤x∗ij≤1
- 此外: 还有对数变换, 平方根变换, 立方根变换等, 主要作用是把非线性数据结构变为 线性结构, 以适应某些统计方法的需要
- 样本间的距离和相似系数
描述样品间的亲疏程度常用距离度量, 常用的距离有
- 闵科夫斯基距离
dij(q)=[∑t=1n|xit−xjt|q]1/q,i,j=1,⋯,n
- q=2 时为欧式距离,为聚类分析中最广泛的距离
dij(2)=∑i=1n(xit−xjt)2−−−−−−−−−−−−√
- 闵科夫斯基距离的其他情形
- q=1 时为绝对距离,
dij(q)=∑t=1n|xit−xjt|,i,j=1,⋯,n
- q=∞ 时称为切比雪夫距离
dij(∞)=max1≤t≤m|xit−xjt|
- 其他常用的距离
- 兰氏距离
dij(L)=1m∑t=1n|xit−xjt|xit+xjt,i,j=1,⋯,n
是一个无量纲的量
- 马氏距离(Mahalanobis) 聚类分析中最常用的距离方法
样品 X(i),X(j) 的马氏距离为
dij(M)=(X(i)−X(j))′S−1(X(i)−X(j))
其中 S 为样本协方差矩阵, 马氏距离可以排除变量之间相关性的影响, 并且不受量纲的 影响
- 变量间的相似系数和距离
聚类分析方法不仅用来对样品进行分类, 有时需要对变量进行分类。
- 变量间的亲疏程度一般采用相似系数来表示、
- 设 Cij 表示两个变量 Xi,Xj 之间的相似系数, 一般要求:
- Cij=±1⇔Xi=aXj
- |Cij|≤1 , 对一切 i,j 成立
- Cij=Cji , 对一切 i,j 成立
对于定量变量, 常用的相似系数有夹角余弦和相关系数。
- 夹角余弦
设变量 Xi=(xi1,xi2,⋯,xin) ,看做是n维空间中的向量, 则 Xi,Xj 夹角余弦称为两向量的相似系数, 记为
cij=∑i=1nxtixtj∑i=1nx2ti−−−−−−√∑i=1nx2tj−−−−−−√
Cij=1 时, 说明两向量完全相似, 当 Xi,Xj 正交时, Cij=0 ,
- 相关系数
相关系数就是对数据作标准化处理后的夹角余弦, 变量 Xi,Xj 的相关系数常用 rij 表示
rij=∑i=1n(xti−x¯i)(xtj−x¯j)∑t=1n(xti−x¯i)2−−−−−−−−−−−√∑t=1n(xtj−x¯j)−−−−−−−−−−−√
- 变量间距离的定义
- 利用相似系数来定义变量间的距离
dij=1−|Cij|或d2ij=1−C2ij
- 利用样本协方差阵定义距离 设样本协方差阵为 S=(sij) ,变量 Xi,Xj 间的距离可定义为
dij=sii+sjj−2sij
- 把变量看做n维欧式空间中的点, 类似样品间距离定义变量间的距离
- 系统聚类法
系统聚类发是目前在实际应用中使用最多的一类方法, 是将类由多变到少的一种方法
- 系统聚类法的基本思想
设有n个样品, 系统聚类方法的基本思想是:
- 首先定义样品间的距离(或相似系数) 和类与类之间的距离( 后面有详细说明 )。
- n个样品自成一类, 此时类间的距离与样品间的距离是等价的
- 将距离最近的两类合并, 并计算新类到其他类的类间距离, 再按照最小距离准则合并
- 每次缩小一类, 直到所有的样品都并成一类为止
- 通过谱系聚类图描述出并类过程
- 系统聚类分析的方法–类间距离
- 系统聚类法的聚类方法主要取决于样品间的距离和类间距离的定义
- 类间距离的不同定义就产生了不同的系统聚类分析方法。
- 常见的类间距离定义有
- 最短距离法、
- 最长距离法
- 重心法
- 中间距离法, 类平均法, 可变平均法等
- 最短距离法
记 dij 为样品 Xi,Xj 之间的距离, 类 Gp 与类 Gq 之间的距离定义为两类 中最近样品的距离, 即
Dpq=mini∈Gp,j∈Gqdij
其中 i∈Gp 表示 Xi∈Gp
- 递推公式
当某步 Gp 与 Gq 合并为 Gr 后, 按最短距离法计算新类 Gr 其他类 Gk 之间的距离时, 有
Drk=min(Dpk,Dqk)
- 最长距离法
类与类之间的距离定义为两类中距离最远的两个样品间的距离, 即
Dpq=maxi∈Gp,j∈Gqdij
- 递推公式
若 Gr=Gp∪Gq , 则对任意的 Gk ,有 Drk=max(Dpk,Dqk)
- 重心法
- 上面的两种距离没有考虑每一类中所包含的样品个数
- 如果将两类间的距离定义为两类重心间的距离, 这种聚类方法称为重心法,
- 设 Gp 中样品量为 np ,重心为 X¯(p) , Gq 的样品量为 nq ,重心为 X¯(q) ,则定义两类间的距离为
Dpq=d(X¯(p),X¯(q))
- 设两类合并后的新类为 Gr , 样品量 nr=np+nq , 重心为 X¯(r) ,则有
X¯(r)=1nr(npX¯(p)+nqX¯(q))
- 类个数的确定
聚类分析汇总, 类的个数的确定是个十分困难的问题, 人们至今仍未找到满意的方法, Brmirmen (1972) 提出根据谱系图来分析的准则
- 准则A: 各类重心之间的距离必须很大
- 准则B: 确定的类中, 各类所包含的元素都不要太多
- 准则C: 类的个数必须符合使用目的
- 准则D:若采用不同的聚类方法处理, 则在各自的聚类图中应发现相同的类
- 聚类分析操作演示
数据 小康指数.sav 记录了31个省份的指标, 包括 综合指数, 社会结构, 经济与技术发展, 人口素质, 生活质量, 法制与治安六项指标,
- 就这六 项指标对31个省份进行聚类分析, 类别个数取3-5个,
- 输出每类的重心
- 分析聚类结果
3 聚类分析实现(using R)
- 系统聚类方法实现值
hclust 函数
- 用法
hclust(d,...)
- 其中 d 是
dist() 生成的距离下三角矩阵
- 选项
method 表示聚类的方法, 指的是类间距离的定义方法, 一般有
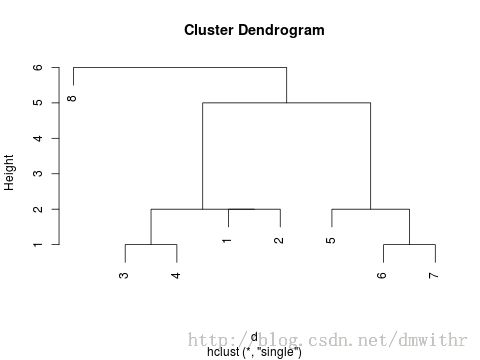
- single 单连接, 最短距离法
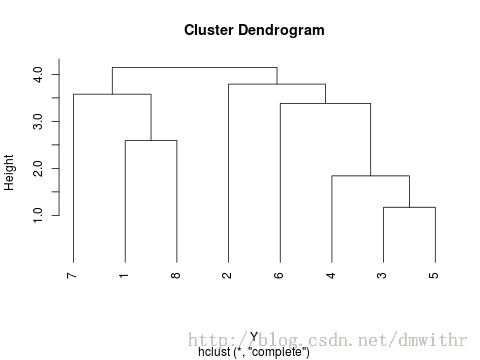
- comlete 完全连接, 最长距离法
- average 平均距离法
- centroid 重心法
- R实现聚类分析示例一
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
V1 V2 V3 V4 V5
1 7.90 39.77 8.49 12.94 19.27
2 11.05 2.04 13.29 7.68 50.37
3 11.35 13.30 19.25 14.59 2.75
4 14.87 9.42 27.93 8.20 8.14
5 16.17 9.42 15.55 9.76 9.16
6 27.98 9.01 9.32 15.99 9.10
7 1.82 11.35 10.06 28.64 10.52
8 10.05 16.18 8.39 1.96 10.81
- 程序代码
- 聚类谱系图
- 示例二
Call:
hclust(d = d, method = "single")
Cluster method : single
Distance : manhattan
Number of objects: 8
- 谱系图
4 聚类分析实现(Using Matlab)
- 层次聚类分析的matlab实现
层次聚类法的计算步骤如下
- 计算n个样本两两间的距离 dij 记为D
- 构造 n个类, 每个类只包含一个样本
- 合并距离最近的两个类为一个新类
- 计算新类与当前各类的距离, 若类的个数等于1, 则转到5, 否则回到3
- 绘制聚类图
- 决定类的个数和每个类
- Matlab中与聚类相关的主要函数和功能
函数
功能
clusterdata从数据集合 x 中创建聚类
cluster从linkage中创建聚类
linkage计算数据集中的目标为二元群的层次树
pdist计算数据集合中两两元素间的距离(向量)
dendrogram画出系统聚类图
squareform将距离的输出向量形式定格为矩阵形式
zscore对数据局进行标准化处理
- 函数用法
T=clusterdata(x,cutoff) X为数据矩阵, cutoff 是创建聚类的临界点, 即表示欲分为多少个类别T=cluster(Z,cutoff) 从逐级聚类树中构造聚类, 其中Z是由语句 linkage 产生的 (n-1)x3 矩阵, cutoff 是 创建聚类的临界值Z=linkage(Y) 或 Z=linkage(Y,'method') 创建逐级聚类树, 其中 Y 为有 pdist 产生 的长度为 n(n-1)/2 的距离向量, 其中 method 表示所有的类间距离定义方法, 默认为 "最近距离" simple, 可以采用 complete –"最长距离法", average类平均 法, weight "加权平均距离" 等
- 函数用法
Y=pdist(X,distance), distance 表示距离选型
- 默认为 欧式距离
enclidean ,
- 标准欧式 距离
seuclid
- 马氏距离
mahalanobis
- 闵可夫斯基距离
minkowski 须加参数 q
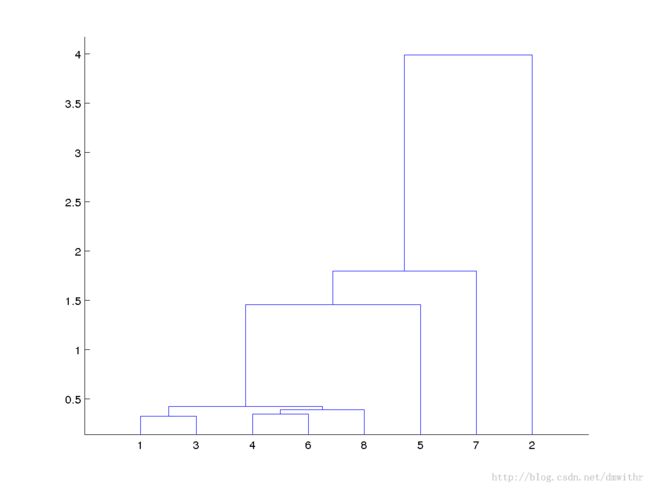
H=dendrogram(Z) 对 linkage 产生的数据矩阵 Z 绘制谱系聚类图
- 示例
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
7.90
39.77
8.49
12.94
19.27
11.05
2.04
13.29
7.68
50.37
11.35
13.30
19.25
14.59
2.75
14.87
9.42
27.93
8.20
8.14
16.17
9.42
15.55
9.76
9.16
27.98
9.01
9.32
15.99
9.10
1.82
11.35
10.06
28.64
10.52
10.05
16.18
8.39
1.96
10.81
- 程序代码
x=[7.90,39.77,8.49,12.94,19.27,11.05,2.04,13.29;
7.68,50.37,11.35,13.30,19.25,14.59,2.75,14.87;
9.42,27.93,8.20,8.14,16.17,9.42,15.55,9.76;
9.16,27.98,9.01,9.32,15.99,9.10,1.82,11.35;
10.06,28.64,10.52,10.05,16.18,8.39,1.96,10.81];
X=zscore(x');
Y=pdist(X);
D=squareform(Y);
Z=linkage(Y)
Z =
1.0000 3.0000 0.3214
4.0000 6.0000 0.3432
8.0000 10.0000 0.3876
9.0000 11.0000 0.4191
5.0000 12.0000 1.4527
7.0000 13.0000 1.7937
2.0000 14.0000 3.9904
T=cluster(Z,3);
find(T==3)
ans =
2
- Iris 数据的聚类分析
ans =
0 0 2
0 50 48
50 0 0
可以看出聚类的效果并不好, Fisher判别分析可以比较好的对样品进行分割
聚类分析
Table of Contents
- 1. 聚类分析的内容和方法
- 2. 距离和相似度
- 3. 聚类分析实现(using R)
- 4. 聚类分析实现(Using Matlab)
1 聚类分析的内容和方法
- 聚类分析的背景
- 聚类分析也称为群分析, 是研究对样品或指标进行分类的一种多元统计方法
- 在实际问题中, 经常遇到分类问题,
- 大气污染的轻重区域,
- 在经济学中, 根据人均国 民收入, 人均工农业产值, 人均消费水平等多种指标对各个国家的经济发展状况进 行分类等,
- 个人进行股市投资时, 会有选择性的把股市上的股票分为几种, 潜力股, 垃 圾股等,
- 聚类分析和判别分析之间的关系: 判别分析是已知类别及性质, 对新样本进行归类, 而聚类 分析是对待分析的数据不知道该分为几类, 需要从样本数据出发进行分析
- 在机器学习, 聚类分析属于无指导的机器学习
- 聚类分析的内容十分丰富, 按照聚类方法有如下几种
- 系统聚类法:开始每个对象自成一类, 然后每次将最近似的两类进行, 合并后重新 计算新类与其他类之间的距离或相似程度, 一直持续进行到所有对象合并为一类
- 可以通过一张谱系图进行描述聚类的过程
- 模糊聚类法:利用模糊集理论来处理分类问题, 对经济领域中具有模糊特征的两态数据或 多态数据具有较好的分类效果
- 最优分割法, 调优法(动态聚类法), 图论聚类法等方法
- 聚类分析分类对象
- 聚类分析按照分类对象不同分为两类
- 变量聚类:可以了解变量间及变量组合间的亲疏关系根据分类结果及他们之间的关系, 在每一类中选择有代表性的变量
- 样品聚类对样品进行分类, 分类的结果是直观的, 且比传统方法更细致, 全面, 但是对 任何观测数据 都没有唯一“正确的”分类方法
- 本课程重点是 系统聚类法, 且主要讨论样品聚类问题
2 距离和相似度
- 原始样本数据
- 设有n个样本, 每个样本测得m个指标, 得观测数据为 xij,i=1,⋯,n,j=1,⋯,m
- 计算第j个指标的均值和标准差, 极差
- x¯j=1n∑i=1nxij
- sj=1n−1∑i=1n(xij−x¯j)2−−−−−−−−−−−−−−−−√, j=1,⋯,m
- Rj=max(xij,i=1,⋯,n)−min(xij,i=1,⋯,n)
- 数据预处理–数据变换
- 数据在进行聚类之前因为量纲不同, 将影响样品间的距离计算和类间距离的计算, 需 要进行适当的变换
- 中心化变换 (对每个变量) x∗ij=xij−x¯j ,变换后数据的均值为0, 协方差阵不变
S∗=(sij), sij=1n−1∑t=1n(xti−x¯i)(xtj−x¯j)=1n−1∑t=1nx∗tix∗tj
- 标准化变换
x∗ij=xij−x¯jsj,i=1,⋯,n,j=1,⋯,m
变换后的数据, 均值为0, 标准差为1, 也称为 Zcore 变换
- 极差变换
- 极差标准化变换
x∗ij=xij−x¯jRj
变换后的数据, 每个变量的样本均值为0, 极差为1, 且 |x∗ij|<1
- 极差正规化变换
x∗ij=xij−min1≤t≤nxtjRj
变换之后的数据 0≤x∗ij≤1
- 此外: 还有对数变换, 平方根变换, 立方根变换等, 主要作用是把非线性数据结构变为 线性结构, 以适应某些统计方法的需要
- 样本间的距离和相似系数
描述样品间的亲疏程度常用距离度量, 常用的距离有
- 闵科夫斯基距离
dij(q)=[∑t=1n|xit−xjt|q]1/q,i,j=1,⋯,n
- q=2 时为欧式距离,为聚类分析中最广泛的距离
dij(2)=∑i=1n(xit−xjt)2−−−−−−−−−−−−√
- 闵科夫斯基距离的其他情形
- q=1 时为绝对距离,
dij(q)=∑t=1n|xit−xjt|,i,j=1,⋯,n
- q=∞ 时称为切比雪夫距离
dij(∞)=max1≤t≤m|xit−xjt|
- 其他常用的距离
- 兰氏距离
dij(L)=1m∑t=1n|xit−xjt|xit+xjt,i,j=1,⋯,n
是一个无量纲的量
- 马氏距离(Mahalanobis) 聚类分析中最常用的距离方法
样品 X(i),X(j) 的马氏距离为
dij(M)=(X(i)−X(j))′S−1(X(i)−X(j))
其中 S 为样本协方差矩阵, 马氏距离可以排除变量之间相关性的影响, 并且不受量纲的 影响
- 变量间的相似系数和距离
聚类分析方法不仅用来对样品进行分类, 有时需要对变量进行分类。
- 变量间的亲疏程度一般采用相似系数来表示、
- 设 Cij 表示两个变量 Xi,Xj 之间的相似系数, 一般要求:
- Cij=±1⇔Xi=aXj
- |Cij|≤1 , 对一切 i,j 成立
- Cij=Cji , 对一切 i,j 成立
对于定量变量, 常用的相似系数有夹角余弦和相关系数。
- 夹角余弦
设变量 Xi=(xi1,xi2,⋯,xin) ,看做是n维空间中的向量, 则 Xi,Xj 夹角余弦称为两向量的相似系数, 记为
cij=∑i=1nxtixtj∑i=1nx2ti−−−−−−√∑i=1nx2tj−−−−−−√
Cij=1 时, 说明两向量完全相似, 当 Xi,Xj 正交时, Cij=0 ,
- 相关系数
相关系数就是对数据作标准化处理后的夹角余弦, 变量 Xi,Xj 的相关系数常用 rij 表示
rij=∑i=1n(xti−x¯i)(xtj−x¯j)∑t=1n(xti−x¯i)2−−−−−−−−−−−√∑t=1n(xtj−x¯j)−−−−−−−−−−−√
- 变量间距离的定义
- 利用相似系数来定义变量间的距离
dij=1−|Cij|或d2ij=1−C2ij
- 利用样本协方差阵定义距离 设样本协方差阵为 S=(sij) ,变量 Xi,Xj 间的距离可定义为
dij=sii+sjj−2sij
- 把变量看做n维欧式空间中的点, 类似样品间距离定义变量间的距离
- 系统聚类法
系统聚类发是目前在实际应用中使用最多的一类方法, 是将类由多变到少的一种方法
- 系统聚类法的基本思想
设有n个样品, 系统聚类方法的基本思想是:
- 首先定义样品间的距离(或相似系数) 和类与类之间的距离( 后面有详细说明 )。
- n个样品自成一类, 此时类间的距离与样品间的距离是等价的
- 将距离最近的两类合并, 并计算新类到其他类的类间距离, 再按照最小距离准则合并
- 每次缩小一类, 直到所有的样品都并成一类为止
- 通过谱系聚类图描述出并类过程
- 系统聚类分析的方法–类间距离
- 系统聚类法的聚类方法主要取决于样品间的距离和类间距离的定义
- 类间距离的不同定义就产生了不同的系统聚类分析方法。
- 常见的类间距离定义有
- 最短距离法、
- 最长距离法
- 重心法
- 中间距离法, 类平均法, 可变平均法等
- 最短距离法
记 dij 为样品 Xi,Xj 之间的距离, 类 Gp 与类 Gq 之间的距离定义为两类 中最近样品的距离, 即
Dpq=mini∈Gp,j∈Gqdij
其中 i∈Gp 表示 Xi∈Gp
- 递推公式
当某步 Gp 与 Gq 合并为 Gr 后, 按最短距离法计算新类 Gr 其他类 Gk 之间的距离时, 有
Drk=min(Dpk,Dqk)
- 最长距离法
类与类之间的距离定义为两类中距离最远的两个样品间的距离, 即
Dpq=maxi∈Gp,j∈Gqdij
- 递推公式
若 Gr=Gp∪Gq , 则对任意的 Gk ,有 Drk=max(Dpk,Dqk)
- 重心法
- 上面的两种距离没有考虑每一类中所包含的样品个数
- 如果将两类间的距离定义为两类重心间的距离, 这种聚类方法称为重心法,
- 设 Gp 中样品量为 np ,重心为 X¯(p) , Gq 的样品量为 nq ,重心为 X¯(q) ,则定义两类间的距离为
Dpq=d(X¯(p),X¯(q))
- 设两类合并后的新类为 Gr , 样品量 nr=np+nq , 重心为 X¯(r) ,则有
X¯(r)=1nr(npX¯(p)+nqX¯(q))
- 类个数的确定
聚类分析汇总, 类的个数的确定是个十分困难的问题, 人们至今仍未找到满意的方法, Brmirmen (1972) 提出根据谱系图来分析的准则
- 准则A: 各类重心之间的距离必须很大
- 准则B: 确定的类中, 各类所包含的元素都不要太多
- 准则C: 类的个数必须符合使用目的
- 准则D:若采用不同的聚类方法处理, 则在各自的聚类图中应发现相同的类
- 聚类分析操作演示
数据 小康指数.sav 记录了31个省份的指标, 包括 综合指数, 社会结构, 经济与技术发展, 人口素质, 生活质量, 法制与治安六项指标,
- 就这六 项指标对31个省份进行聚类分析, 类别个数取3-5个,
- 输出每类的重心
- 分析聚类结果
3 聚类分析实现(using R)
- 系统聚类方法实现值
hclust 函数
- 用法
hclust(d,...)
- 其中 d 是
dist() 生成的距离下三角矩阵
- 选项
method 表示聚类的方法, 指的是类间距离的定义方法, 一般有
- single 单连接, 最短距离法
- comlete 完全连接, 最长距离法
- average 平均距离法
- centroid 重心法
- R实现聚类分析示例一
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
V1 V2 V3 V4 V5
1 7.90 39.77 8.49 12.94 19.27
2 11.05 2.04 13.29 7.68 50.37
3 11.35 13.30 19.25 14.59 2.75
4 14.87 9.42 27.93 8.20 8.14
5 16.17 9.42 15.55 9.76 9.16
6 27.98 9.01 9.32 15.99 9.10
7 1.82 11.35 10.06 28.64 10.52
8 10.05 16.18 8.39 1.96 10.81
- 程序代码
- 聚类谱系图
- 示例二
Call:
hclust(d = d, method = "single")
Cluster method : single
Distance : manhattan
Number of objects: 8
- 谱系图
4 聚类分析实现(Using Matlab)
- 层次聚类分析的matlab实现
层次聚类法的计算步骤如下
- 计算n个样本两两间的距离 dij 记为D
- 构造 n个类, 每个类只包含一个样本
- 合并距离最近的两个类为一个新类
- 计算新类与当前各类的距离, 若类的个数等于1, 则转到5, 否则回到3
- 绘制聚类图
- 决定类的个数和每个类
- Matlab中与聚类相关的主要函数和功能
函数
功能
clusterdata从数据集合 x 中创建聚类
cluster从linkage中创建聚类
linkage计算数据集中的目标为二元群的层次树
pdist计算数据集合中两两元素间的距离(向量)
dendrogram画出系统聚类图
squareform将距离的输出向量形式定格为矩阵形式
zscore对数据局进行标准化处理
- 函数用法
T=clusterdata(x,cutoff) X为数据矩阵, cutoff 是创建聚类的临界点, 即表示欲分为多少个类别T=cluster(Z,cutoff) 从逐级聚类树中构造聚类, 其中Z是由语句 linkage 产生的 (n-1)x3 矩阵, cutoff 是 创建聚类的临界值Z=linkage(Y) 或 Z=linkage(Y,'method') 创建逐级聚类树, 其中 Y 为有 pdist 产生 的长度为 n(n-1)/2 的距离向量, 其中 method 表示所有的类间距离定义方法, 默认为 "最近距离" simple, 可以采用 complete –"最长距离法", average类平均 法, weight "加权平均距离" 等
- 函数用法
Y=pdist(X,distance), distance 表示距离选型
- 默认为 欧式距离
enclidean ,
- 标准欧式 距离
seuclid
- 马氏距离
mahalanobis
- 闵可夫斯基距离
minkowski 须加参数 q
H=dendrogram(Z) 对 linkage 产生的数据矩阵 Z 绘制谱系聚类图
- 示例
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
7.90
39.77
8.49
12.94
19.27
11.05
2.04
13.29
7.68
50.37
11.35
13.30
19.25
14.59
2.75
14.87
9.42
27.93
8.20
8.14
16.17
9.42
15.55
9.76
9.16
27.98
9.01
9.32
15.99
9.10
1.82
11.35
10.06
28.64
10.52
10.05
16.18
8.39
1.96
10.81
- 程序代码
x=[7.90,39.77,8.49,12.94,19.27,11.05,2.04,13.29;
7.68,50.37,11.35,13.30,19.25,14.59,2.75,14.87;
9.42,27.93,8.20,8.14,16.17,9.42,15.55,9.76;
9.16,27.98,9.01,9.32,15.99,9.10,1.82,11.35;
10.06,28.64,10.52,10.05,16.18,8.39,1.96,10.81];
X=zscore(x');
Y=pdist(X);
D=squareform(Y);
Z=linkage(Y)
Z =
1.0000 3.0000 0.3214
4.0000 6.0000 0.3432
8.0000 10.0000 0.3876
9.0000 11.0000 0.4191
5.0000 12.0000 1.4527
7.0000 13.0000 1.7937
2.0000 14.0000 3.9904
T=cluster(Z,3);
find(T==3)
ans =
2
- Iris 数据的聚类分析
ans =
0 0 2
0 50 48
50 0 0
可以看出聚类的效果并不好, Fisher判别分析可以比较好的对样品进行分割
聚类分析
Table of Contents
- 1. 聚类分析的内容和方法
- 2. 距离和相似度
- 3. 聚类分析实现(using R)
- 4. 聚类分析实现(Using Matlab)
1 聚类分析的内容和方法
- 聚类分析的背景
- 聚类分析也称为群分析, 是研究对样品或指标进行分类的一种多元统计方法
- 在实际问题中, 经常遇到分类问题,
- 大气污染的轻重区域,
- 在经济学中, 根据人均国 民收入, 人均工农业产值, 人均消费水平等多种指标对各个国家的经济发展状况进 行分类等,
- 个人进行股市投资时, 会有选择性的把股市上的股票分为几种, 潜力股, 垃 圾股等,
- 聚类分析和判别分析之间的关系: 判别分析是已知类别及性质, 对新样本进行归类, 而聚类 分析是对待分析的数据不知道该分为几类, 需要从样本数据出发进行分析
- 在机器学习, 聚类分析属于无指导的机器学习
- 聚类分析的内容十分丰富, 按照聚类方法有如下几种
- 系统聚类法:开始每个对象自成一类, 然后每次将最近似的两类进行, 合并后重新 计算新类与其他类之间的距离或相似程度, 一直持续进行到所有对象合并为一类
- 可以通过一张谱系图进行描述聚类的过程
- 模糊聚类法:利用模糊集理论来处理分类问题, 对经济领域中具有模糊特征的两态数据或 多态数据具有较好的分类效果
- 最优分割法, 调优法(动态聚类法), 图论聚类法等方法
- 聚类分析分类对象
- 聚类分析按照分类对象不同分为两类
- 变量聚类:可以了解变量间及变量组合间的亲疏关系根据分类结果及他们之间的关系, 在每一类中选择有代表性的变量
- 样品聚类对样品进行分类, 分类的结果是直观的, 且比传统方法更细致, 全面, 但是对 任何观测数据 都没有唯一“正确的”分类方法
- 本课程重点是 系统聚类法, 且主要讨论样品聚类问题
2 距离和相似度
- 原始样本数据
- 设有n个样本, 每个样本测得m个指标, 得观测数据为 xij,i=1,⋯,n,j=1,⋯,m
- 计算第j个指标的均值和标准差, 极差
- x¯j=1n∑i=1nxij
- sj=1n−1∑i=1n(xij−x¯j)2−−−−−−−−−−−−−−−−√, j=1,⋯,m
- Rj=max(xij,i=1,⋯,n)−min(xij,i=1,⋯,n)
- 数据预处理–数据变换
- 数据在进行聚类之前因为量纲不同, 将影响样品间的距离计算和类间距离的计算, 需 要进行适当的变换
- 中心化变换 (对每个变量) x∗ij=xij−x¯j ,变换后数据的均值为0, 协方差阵不变
S∗=(sij), sij=1n−1∑t=1n(xti−x¯i)(xtj−x¯j)=1n−1∑t=1nx∗tix∗tj
- 标准化变换
x∗ij=xij−x¯jsj,i=1,⋯,n,j=1,⋯,m
变换后的数据, 均值为0, 标准差为1, 也称为 Zcore 变换
- 极差变换
- 极差标准化变换
x∗ij=xij−x¯jRj
变换后的数据, 每个变量的样本均值为0, 极差为1, 且 |x∗ij|<1
- 极差正规化变换
x∗ij=xij−min1≤t≤nxtjRj
变换之后的数据 0≤x∗ij≤1
- 此外: 还有对数变换, 平方根变换, 立方根变换等, 主要作用是把非线性数据结构变为 线性结构, 以适应某些统计方法的需要
- 样本间的距离和相似系数
描述样品间的亲疏程度常用距离度量, 常用的距离有
- 闵科夫斯基距离
dij(q)=[∑t=1n|xit−xjt|q]1/q,i,j=1,⋯,n
- q=2 时为欧式距离,为聚类分析中最广泛的距离
dij(2)=∑i=1n(xit−xjt)2−−−−−−−−−−−−√
- 闵科夫斯基距离的其他情形
- q=1 时为绝对距离,
dij(q)=∑t=1n|xit−xjt|,i,j=1,⋯,n
- q=∞ 时称为切比雪夫距离
dij(∞)=max1≤t≤m|xit−xjt|
- 其他常用的距离
- 兰氏距离
dij(L)=1m∑t=1n|xit−xjt|xit+xjt,i,j=1,⋯,n
是一个无量纲的量
- 马氏距离(Mahalanobis) 聚类分析中最常用的距离方法
样品 X(i),X(j) 的马氏距离为
dij(M)=(X(i)−X(j))′S−1(X(i)−X(j))
其中 S 为样本协方差矩阵, 马氏距离可以排除变量之间相关性的影响, 并且不受量纲的 影响
- 变量间的相似系数和距离
聚类分析方法不仅用来对样品进行分类, 有时需要对变量进行分类。
- 变量间的亲疏程度一般采用相似系数来表示、
- 设 Cij 表示两个变量 Xi,Xj 之间的相似系数, 一般要求:
- Cij=±1⇔Xi=aXj
- |Cij|≤1 , 对一切 i,j 成立
- Cij=Cji , 对一切 i,j 成立
对于定量变量, 常用的相似系数有夹角余弦和相关系数。
- 夹角余弦
设变量 Xi=(xi1,xi2,⋯,xin) ,看做是n维空间中的向量, 则 Xi,Xj 夹角余弦称为两向量的相似系数, 记为
cij=∑i=1nxtixtj∑i=1nx2ti−−−−−−√∑i=1nx2tj−−−−−−√
Cij=1 时, 说明两向量完全相似, 当 Xi,Xj 正交时, Cij=0 ,
- 相关系数
相关系数就是对数据作标准化处理后的夹角余弦, 变量 Xi,Xj 的相关系数常用 rij 表示
rij=∑i=1n(xti−x¯i)(xtj−x¯j)∑t=1n(xti−x¯i)2−−−−−−−−−−−√∑t=1n(xtj−x¯j)−−−−−−−−−−−√
- 变量间距离的定义
- 利用相似系数来定义变量间的距离
dij=1−|Cij|或d2ij=1−C2ij
- 利用样本协方差阵定义距离 设样本协方差阵为 S=(sij) ,变量 Xi,Xj 间的距离可定义为
dij=sii+sjj−2sij
- 把变量看做n维欧式空间中的点, 类似样品间距离定义变量间的距离
- 系统聚类法
系统聚类发是目前在实际应用中使用最多的一类方法, 是将类由多变到少的一种方法
- 系统聚类法的基本思想
设有n个样品, 系统聚类方法的基本思想是:
- 首先定义样品间的距离(或相似系数) 和类与类之间的距离( 后面有详细说明 )。
- n个样品自成一类, 此时类间的距离与样品间的距离是等价的
- 将距离最近的两类合并, 并计算新类到其他类的类间距离, 再按照最小距离准则合并
- 每次缩小一类, 直到所有的样品都并成一类为止
- 通过谱系聚类图描述出并类过程
- 系统聚类分析的方法–类间距离
- 系统聚类法的聚类方法主要取决于样品间的距离和类间距离的定义
- 类间距离的不同定义就产生了不同的系统聚类分析方法。
- 常见的类间距离定义有
- 最短距离法、
- 最长距离法
- 重心法
- 中间距离法, 类平均法, 可变平均法等
- 最短距离法
记 dij 为样品 Xi,Xj 之间的距离, 类 Gp 与类 Gq 之间的距离定义为两类 中最近样品的距离, 即
Dpq=mini∈Gp,j∈Gqdij
其中 i∈Gp 表示 Xi∈Gp
- 递推公式
当某步 Gp 与 Gq 合并为 Gr 后, 按最短距离法计算新类 Gr 其他类 Gk 之间的距离时, 有
Drk=min(Dpk,Dqk)
- 最长距离法
类与类之间的距离定义为两类中距离最远的两个样品间的距离, 即
Dpq=maxi∈Gp,j∈Gqdij
- 递推公式
若 Gr=Gp∪Gq , 则对任意的 Gk ,有 Drk=max(Dpk,Dqk)
- 重心法
- 上面的两种距离没有考虑每一类中所包含的样品个数
- 如果将两类间的距离定义为两类重心间的距离, 这种聚类方法称为重心法,
- 设 Gp 中样品量为 np ,重心为 X¯(p) , Gq 的样品量为 nq ,重心为 X¯(q) ,则定义两类间的距离为
Dpq=d(X¯(p),X¯(q))
- 设两类合并后的新类为 Gr , 样品量 nr=np+nq , 重心为 X¯(r) ,则有
X¯(r)=1nr(npX¯(p)+nqX¯(q))
- 类个数的确定
聚类分析汇总, 类的个数的确定是个十分困难的问题, 人们至今仍未找到满意的方法, Brmirmen (1972) 提出根据谱系图来分析的准则
- 准则A: 各类重心之间的距离必须很大
- 准则B: 确定的类中, 各类所包含的元素都不要太多
- 准则C: 类的个数必须符合使用目的
- 准则D:若采用不同的聚类方法处理, 则在各自的聚类图中应发现相同的类
- 聚类分析操作演示
数据 小康指数.sav 记录了31个省份的指标, 包括 综合指数, 社会结构, 经济与技术发展, 人口素质, 生活质量, 法制与治安六项指标,
- 就这六 项指标对31个省份进行聚类分析, 类别个数取3-5个,
- 输出每类的重心
- 分析聚类结果
3 聚类分析实现(using R)
- 系统聚类方法实现值
hclust 函数
- 用法
hclust(d,...)
- 其中 d 是
dist() 生成的距离下三角矩阵
- 选项
method 表示聚类的方法, 指的是类间距离的定义方法, 一般有
- single 单连接, 最短距离法
- comlete 完全连接, 最长距离法
- average 平均距离法
- centroid 重心法
- R实现聚类分析示例一
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
V1 V2 V3 V4 V5
1 7.90 39.77 8.49 12.94 19.27
2 11.05 2.04 13.29 7.68 50.37
3 11.35 13.30 19.25 14.59 2.75
4 14.87 9.42 27.93 8.20 8.14
5 16.17 9.42 15.55 9.76 9.16
6 27.98 9.01 9.32 15.99 9.10
7 1.82 11.35 10.06 28.64 10.52
8 10.05 16.18 8.39 1.96 10.81
- 程序代码
- 聚类谱系图
- 示例二
Call:
hclust(d = d, method = "single")
Cluster method : single
Distance : manhattan
Number of objects: 8
- 谱系图
4 聚类分析实现(Using Matlab)
- 层次聚类分析的matlab实现
层次聚类法的计算步骤如下
- 计算n个样本两两间的距离 dij 记为D
- 构造 n个类, 每个类只包含一个样本
- 合并距离最近的两个类为一个新类
- 计算新类与当前各类的距离, 若类的个数等于1, 则转到5, 否则回到3
- 绘制聚类图
- 决定类的个数和每个类
- Matlab中与聚类相关的主要函数和功能
函数
功能
clusterdata从数据集合 x 中创建聚类
cluster从linkage中创建聚类
linkage计算数据集中的目标为二元群的层次树
pdist计算数据集合中两两元素间的距离(向量)
dendrogram画出系统聚类图
squareform将距离的输出向量形式定格为矩阵形式
zscore对数据局进行标准化处理
- 函数用法
T=clusterdata(x,cutoff) X为数据矩阵, cutoff 是创建聚类的临界点, 即表示欲分为多少个类别T=cluster(Z,cutoff) 从逐级聚类树中构造聚类, 其中Z是由语句 linkage 产生的 (n-1)x3 矩阵, cutoff 是 创建聚类的临界值Z=linkage(Y) 或 Z=linkage(Y,'method') 创建逐级聚类树, 其中 Y 为有 pdist 产生 的长度为 n(n-1)/2 的距离向量, 其中 method 表示所有的类间距离定义方法, 默认为 "最近距离" simple, 可以采用 complete –"最长距离法", average类平均 法, weight "加权平均距离" 等
- 函数用法
Y=pdist(X,distance), distance 表示距离选型
- 默认为 欧式距离
enclidean ,
- 标准欧式 距离
seuclid
- 马氏距离
mahalanobis
- 闵可夫斯基距离
minkowski 须加参数 q
H=dendrogram(Z) 对 linkage 产生的数据矩阵 Z 绘制谱系聚类图
- 示例
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
7.90
39.77
8.49
12.94
19.27
11.05
2.04
13.29
7.68
50.37
11.35
13.30
19.25
14.59
2.75
14.87
9.42
27.93
8.20
8.14
16.17
9.42
15.55
9.76
9.16
27.98
9.01
9.32
15.99
9.10
1.82
11.35
10.06
28.64
10.52
10.05
16.18
8.39
1.96
10.81
- 程序代码
x=[7.90,39.77,8.49,12.94,19.27,11.05,2.04,13.29;
7.68,50.37,11.35,13.30,19.25,14.59,2.75,14.87;
9.42,27.93,8.20,8.14,16.17,9.42,15.55,9.76;
9.16,27.98,9.01,9.32,15.99,9.10,1.82,11.35;
10.06,28.64,10.52,10.05,16.18,8.39,1.96,10.81];
X=zscore(x');
Y=pdist(X);
D=squareform(Y);
Z=linkage(Y)
Z =
1.0000 3.0000 0.3214
4.0000 6.0000 0.3432
8.0000 10.0000 0.3876
9.0000 11.0000 0.4191
5.0000 12.0000 1.4527
7.0000 13.0000 1.7937
2.0000 14.0000 3.9904
T=cluster(Z,3);
find(T==3)
ans =
2
- Iris 数据的聚类分析
ans =
0 0 2
0 50 48
50 0 0
可以看出聚类的效果并不好, Fisher判别分析可以比较好的对样品进行分割
聚类分析
Table of Contents
- 1. 聚类分析的内容和方法
- 2. 距离和相似度
- 3. 聚类分析实现(using R)
- 4. 聚类分析实现(Using Matlab)
1 聚类分析的内容和方法
- 聚类分析的背景
- 聚类分析也称为群分析, 是研究对样品或指标进行分类的一种多元统计方法
- 在实际问题中, 经常遇到分类问题,
- 大气污染的轻重区域,
- 在经济学中, 根据人均国 民收入, 人均工农业产值, 人均消费水平等多种指标对各个国家的经济发展状况进 行分类等,
- 个人进行股市投资时, 会有选择性的把股市上的股票分为几种, 潜力股, 垃 圾股等,
- 聚类分析和判别分析之间的关系: 判别分析是已知类别及性质, 对新样本进行归类, 而聚类 分析是对待分析的数据不知道该分为几类, 需要从样本数据出发进行分析
- 在机器学习, 聚类分析属于无指导的机器学习
- 聚类分析的内容十分丰富, 按照聚类方法有如下几种
- 系统聚类法:开始每个对象自成一类, 然后每次将最近似的两类进行, 合并后重新 计算新类与其他类之间的距离或相似程度, 一直持续进行到所有对象合并为一类
- 可以通过一张谱系图进行描述聚类的过程
- 模糊聚类法:利用模糊集理论来处理分类问题, 对经济领域中具有模糊特征的两态数据或 多态数据具有较好的分类效果
- 最优分割法, 调优法(动态聚类法), 图论聚类法等方法
- 聚类分析分类对象
- 聚类分析按照分类对象不同分为两类
- 变量聚类:可以了解变量间及变量组合间的亲疏关系根据分类结果及他们之间的关系, 在每一类中选择有代表性的变量
- 样品聚类对样品进行分类, 分类的结果是直观的, 且比传统方法更细致, 全面, 但是对 任何观测数据 都没有唯一“正确的”分类方法
- 本课程重点是 系统聚类法, 且主要讨论样品聚类问题
- 聚类分析按照分类对象不同分为两类
2 距离和相似度
- 原始样本数据
- 设有n个样本, 每个样本测得m个指标, 得观测数据为 xij,i=1,⋯,n,j=1,⋯,m
- 计算第j个指标的均值和标准差, 极差
- x¯j=1n∑i=1nxij
- sj=1n−1∑i=1n(xij−x¯j)2−−−−−−−−−−−−−−−−√, j=1,⋯,m
- Rj=max(xij,i=1,⋯,n)−min(xij,i=1,⋯,n)
- 数据预处理–数据变换
- 数据在进行聚类之前因为量纲不同, 将影响样品间的距离计算和类间距离的计算, 需 要进行适当的变换
- 中心化变换 (对每个变量) x∗ij=xij−x¯j ,变换后数据的均值为0, 协方差阵不变
S∗=(sij), sij=1n−1∑t=1n(xti−x¯i)(xtj−x¯j)=1n−1∑t=1nx∗tix∗tj
- 标准化变换
x∗ij=xij−x¯jsj,i=1,⋯,n,j=1,⋯,m
变换后的数据, 均值为0, 标准差为1, 也称为 Zcore 变换
- 极差变换
- 极差标准化变换
x∗ij=xij−x¯jRj变换后的数据, 每个变量的样本均值为0, 极差为1, 且 |x∗ij|<1
- 极差正规化变换
x∗ij=xij−min1≤t≤nxtjRj变换之后的数据 0≤x∗ij≤1
- 此外: 还有对数变换, 平方根变换, 立方根变换等, 主要作用是把非线性数据结构变为 线性结构, 以适应某些统计方法的需要
- 样本间的距离和相似系数
描述样品间的亲疏程度常用距离度量, 常用的距离有
- 闵科夫斯基距离
dij(q)=[∑t=1n|xit−xjt|q]1/q,i,j=1,⋯,n- q=2 时为欧式距离,为聚类分析中最广泛的距离
dij(2)=∑i=1n(xit−xjt)2−−−−−−−−−−−−√
- 闵科夫斯基距离的其他情形
- q=1 时为绝对距离,
dij(q)=∑t=1n|xit−xjt|,i,j=1,⋯,n
- q=∞ 时称为切比雪夫距离
dij(∞)=max1≤t≤m|xit−xjt|
- q=1 时为绝对距离,
- 其他常用的距离
- 兰氏距离
dij(L)=1m∑t=1n|xit−xjt|xit+xjt,i,j=1,⋯,n
是一个无量纲的量
- 兰氏距离
- 马氏距离(Mahalanobis) 聚类分析中最常用的距离方法
样品 X(i),X(j) 的马氏距离为
dij(M)=(X(i)−X(j))′S−1(X(i)−X(j))其中 S 为样本协方差矩阵, 马氏距离可以排除变量之间相关性的影响, 并且不受量纲的 影响
- 变量间的相似系数和距离
聚类分析方法不仅用来对样品进行分类, 有时需要对变量进行分类。
- 变量间的亲疏程度一般采用相似系数来表示、
- 设 Cij 表示两个变量 Xi,Xj 之间的相似系数, 一般要求:
- Cij=±1⇔Xi=aXj
- |Cij|≤1 , 对一切 i,j 成立
- Cij=Cji , 对一切 i,j 成立
对于定量变量, 常用的相似系数有夹角余弦和相关系数。
- 夹角余弦
设变量 Xi=(xi1,xi2,⋯,xin) ,看做是n维空间中的向量, 则 Xi,Xj 夹角余弦称为两向量的相似系数, 记为
cij=∑i=1nxtixtj∑i=1nx2ti−−−−−−√∑i=1nx2tj−−−−−−√Cij=1 时, 说明两向量完全相似, 当 Xi,Xj 正交时, Cij=0 ,
- 相关系数
相关系数就是对数据作标准化处理后的夹角余弦, 变量 Xi,Xj 的相关系数常用 rij 表示
rij=∑i=1n(xti−x¯i)(xtj−x¯j)∑t=1n(xti−x¯i)2−−−−−−−−−−−√∑t=1n(xtj−x¯j)−−−−−−−−−−−√ - 变量间距离的定义
- 利用相似系数来定义变量间的距离
dij=1−|Cij|或d2ij=1−C2ij
- 利用样本协方差阵定义距离 设样本协方差阵为 S=(sij) ,变量 Xi,Xj 间的距离可定义为
dij=sii+sjj−2sij
- 把变量看做n维欧式空间中的点, 类似样品间距离定义变量间的距离
- 利用相似系数来定义变量间的距离
- 系统聚类法
系统聚类发是目前在实际应用中使用最多的一类方法, 是将类由多变到少的一种方法
- 系统聚类法的基本思想
设有n个样品, 系统聚类方法的基本思想是:
- 首先定义样品间的距离(或相似系数) 和类与类之间的距离( 后面有详细说明 )。
- n个样品自成一类, 此时类间的距离与样品间的距离是等价的
- 将距离最近的两类合并, 并计算新类到其他类的类间距离, 再按照最小距离准则合并
- 每次缩小一类, 直到所有的样品都并成一类为止
- 通过谱系聚类图描述出并类过程
- 系统聚类法的基本思想
- 系统聚类分析的方法–类间距离
- 系统聚类法的聚类方法主要取决于样品间的距离和类间距离的定义
- 类间距离的不同定义就产生了不同的系统聚类分析方法。
- 常见的类间距离定义有
- 最短距离法、
- 最长距离法
- 重心法
- 中间距离法, 类平均法, 可变平均法等
- 系统聚类法的聚类方法主要取决于样品间的距离和类间距离的定义
- 最短距离法
记 dij 为样品 Xi,Xj 之间的距离, 类 Gp 与类 Gq 之间的距离定义为两类 中最近样品的距离, 即
Dpq=mini∈Gp,j∈Gqdij其中 i∈Gp 表示 Xi∈Gp
- 递推公式
当某步 Gp 与 Gq 合并为 Gr 后, 按最短距离法计算新类 Gr 其他类 Gk 之间的距离时, 有
Drk=min(Dpk,Dqk)
- 递推公式
- 最长距离法
类与类之间的距离定义为两类中距离最远的两个样品间的距离, 即
Dpq=maxi∈Gp,j∈Gqdij- 递推公式
若 Gr=Gp∪Gq , 则对任意的 Gk ,有 Drk=max(Dpk,Dqk)
- 递推公式
- 重心法
- 上面的两种距离没有考虑每一类中所包含的样品个数
- 如果将两类间的距离定义为两类重心间的距离, 这种聚类方法称为重心法,
- 设 Gp 中样品量为 np ,重心为 X¯(p) , Gq 的样品量为 nq ,重心为 X¯(q) ,则定义两类间的距离为
Dpq=d(X¯(p),X¯(q))
- 设两类合并后的新类为 Gr , 样品量 nr=np+nq , 重心为 X¯(r) ,则有
X¯(r)=1nr(npX¯(p)+nqX¯(q))
- 类个数的确定
聚类分析汇总, 类的个数的确定是个十分困难的问题, 人们至今仍未找到满意的方法, Brmirmen (1972) 提出根据谱系图来分析的准则
- 准则A: 各类重心之间的距离必须很大
- 准则B: 确定的类中, 各类所包含的元素都不要太多
- 准则C: 类的个数必须符合使用目的
- 准则D:若采用不同的聚类方法处理, 则在各自的聚类图中应发现相同的类
- 聚类分析操作演示
数据 小康指数.sav 记录了31个省份的指标, 包括 综合指数, 社会结构, 经济与技术发展, 人口素质, 生活质量, 法制与治安六项指标,
- 就这六 项指标对31个省份进行聚类分析, 类别个数取3-5个,
- 输出每类的重心
- 分析聚类结果
3 聚类分析实现(using R)
- 系统聚类方法实现值
hclust函数
- 用法
hclust(d,...) - 其中 d 是
dist()生成的距离下三角矩阵 - 选项
method表示聚类的方法, 指的是类间距离的定义方法, 一般有- single 单连接, 最短距离法
- comlete 完全连接, 最长距离法
- average 平均距离法
- centroid 重心法
- 用法
- R实现聚类分析示例一
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
V1 V2 V3 V4 V5 1 7.90 39.77 8.49 12.94 19.27 2 11.05 2.04 13.29 7.68 50.37 3 11.35 13.30 19.25 14.59 2.75 4 14.87 9.42 27.93 8.20 8.14 5 16.17 9.42 15.55 9.76 9.16 6 27.98 9.01 9.32 15.99 9.10 7 1.82 11.35 10.06 28.64 10.52 8 10.05 16.18 8.39 1.96 10.81
- 程序代码
- 聚类谱系图
- 示例二
Call: hclust(d = d, method = "single") Cluster method : single Distance : manhattan Number of objects: 8
- 谱系图
4 聚类分析实现(Using Matlab)
- 层次聚类分析的matlab实现
层次聚类法的计算步骤如下
- 计算n个样本两两间的距离 dij 记为D
- 构造 n个类, 每个类只包含一个样本
- 合并距离最近的两个类为一个新类
- 计算新类与当前各类的距离, 若类的个数等于1, 则转到5, 否则回到3
- 绘制聚类图
- 决定类的个数和每个类
- Matlab中与聚类相关的主要函数和功能
函数 功能 clusterdata从数据集合 x 中创建聚类 cluster从linkage中创建聚类 linkage计算数据集中的目标为二元群的层次树 pdist计算数据集合中两两元素间的距离(向量) dendrogram画出系统聚类图 squareform将距离的输出向量形式定格为矩阵形式 zscore对数据局进行标准化处理 - 函数用法
T=clusterdata(x,cutoff)X为数据矩阵,cutoff是创建聚类的临界点, 即表示欲分为多少个类别T=cluster(Z,cutoff)从逐级聚类树中构造聚类, 其中Z是由语句linkage产生的(n-1)x3矩阵,cutoff是 创建聚类的临界值Z=linkage(Y)或Z=linkage(Y,'method')创建逐级聚类树, 其中Y为有pdist产生 的长度为n(n-1)/2的距离向量, 其中method表示所有的类间距离定义方法, 默认为 "最近距离"simple, 可以采用complete–"最长距离法",average类平均 法,weight"加权平均距离" 等
- 函数用法
Y=pdist(X,distance),distance表示距离选型- 默认为 欧式距离
enclidean, - 标准欧式 距离
seuclid - 马氏距离
mahalanobis - 闵可夫斯基距离
minkowski须加参数q
- 默认为 欧式距离
H=dendrogram(Z)对linkage产生的数据矩阵Z绘制谱系聚类图
- 示例
某地区有八个观测点的数据, 关于5个指标的观测数据如下表, 根据最短距离法对观测点进行聚类分析
7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.29 7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.87 9.42 27.93 8.20 8.14 16.17 9.42 15.55 9.76 9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.35 10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.81 - 程序代码
x=[7.90,39.77,8.49,12.94,19.27,11.05,2.04,13.29; 7.68,50.37,11.35,13.30,19.25,14.59,2.75,14.87; 9.42,27.93,8.20,8.14,16.17,9.42,15.55,9.76; 9.16,27.98,9.01,9.32,15.99,9.10,1.82,11.35; 10.06,28.64,10.52,10.05,16.18,8.39,1.96,10.81]; X=zscore(x'); Y=pdist(X); D=squareform(Y); Z=linkage(Y) Z = 1.0000 3.0000 0.3214 4.0000 6.0000 0.3432 8.0000 10.0000 0.3876 9.0000 11.0000 0.4191 5.0000 12.0000 1.4527 7.0000 13.0000 1.7937 2.0000 14.0000 3.9904 T=cluster(Z,3); find(T==3) ans = 2 - Iris 数据的聚类分析
ans = 0 0 2 0 50 48 50 0 0可以看出聚类的效果并不好, Fisher判别分析可以比较好的对样品进行分割