trie树
Trie树
1基本描述
Tire树又称字典树,单词查找树,或者前缀树,是一种用于快速检索的多叉数据结构。
2用途
利用公共前缀来节约存储空间,一般用于构建字典,构建词库,扫描词库匹配。缺点是内存消耗非常大。
3设计之前考虑的一些性质
根节点为空,除他以外的每个子节点都可以不存储字符(只不过要知道哪个字符对应哪个branch,可以用字符映射到对应的分支,一一对应)。存储字符也可以。
单词必须有结尾,所以必须在每个节点处设置结束标记。
根据字符的数目设置好分支数目(也就是指向后面节点的指针数目)。
4具体实现
#define MAX_Bra 10 //最大分支数目,如果字符串是电话号码可以用0到9表示 所以设置10个分支,如果为字母设置26个分支。
struct trie_node{
bool isStr;//字符是否结束,为真时结束,表示是一个字符串
trie_node* branch[MAX_Bra];//表示分支的指针数组,实现要指明哪个字符对应哪个分支,如果是字母,a可以对应0分支//其他类推 'a'-'a'=0 'b'-'a'=1 如果word中字符较多,可以将每个字符转化为唯一的分支下标,就是这样:branch(charsToindex(word[i]))。这里charsToindex(word[i])就是字符对应的分支号了。
trie_node() { isStr = false; memset(next,NULL,sizeof(branch)); }
};
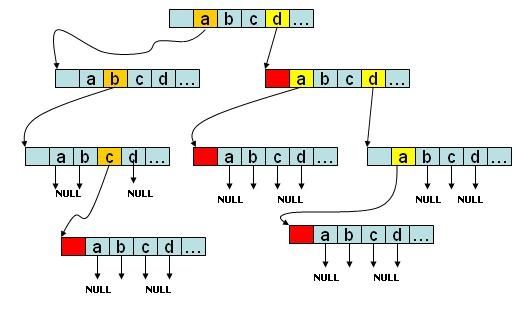
附上一张图,为了更好的理解trie树。
该trie树存有abc、d、da、dda四个字符串,如果是字符串会在节点的尾部进行标记。没有后续字符的branch分支指向NULL
首先定义一个类:Trie_tree,他拥有插入字符串,查找字符串,删除字符串等操作。
class Trie_tree{
public:
Trie_tree();
void insert_word(const char*word);
bool search_word(char*word);
void delete_word(char *word);
private:
trie_node *root;
};
Trie_tree::Trie_tree(){
root = new trie_node();
}
关于插入字符串的操作:
插入时首先匹配字符串的第一个字符,(根据此字符对应的分支下表来匹配,如第一个字符为d,就看分支branch[*word - 'a']是否为空)。为空时表示不存在这个字符,那么动态开辟节点用来存储这个字符。存储到branch[*word - 'a']中。当插入一个字符之后,位置要改变为当前插入的分支,current = current->branch[index];最后达到字符串的尾部,将isStr置为真,表示此处有一个字符串。
简单实现如下:
Trie_tree::insert_word(word){
trie_node *current_node = root;
while (*word)
{
if (current_node->branch[*word-'a'] == NULL)
{
trie_node tmp = new trie_node();
current_node->branch[*word-'a'] = tmp;
}
current_node = current_node->branch[*word-'a'] ;
word++;
}
current_node->isStr = true;//字符串结束之后要设置标志位
}
字符串的查找操作:
根据字符对应的指针不断的向下遍历树的分支,如果能够找到,则对应的节点不为空并且它的isStr标志位为真。
Trie_tree::search_word(char*word){
trie_node *current_node = root;
while (*word&¤t_node)
{
current_node = current_node[*word-'a'];
word++;
}
return (current_node!=NULL&¤t_node->isStr);
}
字符串的删除
首先要找到字符串,如果存在就删除,如果不存在就报错。如何删除呢?
如果字符串是别的词汇的前缀,那么直接销毁最后一个字符的分支的标志位,表示不存在这个字符了。否则,从字符串的最后一个字符回溯上去,找到第一个有至少两个非空指针的节点,从这个节点开始销毁此字符串后面几个节点。麻烦的就是找出这个分叉节点了。
上面只是简单的实现,利用双数组实现可以大大减小内存的使用具体如下:
http://linux.thai.net/~thep/datrie/datrie.html
6时间复杂度分析
插入和查找的时间复杂度均为O(n),n为字符串的长度。
空间复杂度约为:26*(n1+1)+26*(n2+1)+26*(n3+1)...(表达式因为和单词的前缀有关,如果单词前缀重复的多,用的指针空间应该更小,所以不好准确表示)。
7一些应用
排序:tire树是一颗多叉树,遍历整棵树,输出相应的字符串就是按字典排序的结果。
作为其他数据结构和算法的辅助:如AC自动机和后缀树。
还可以用于字符串检索,字符串的最长公共前缀。
关于应用这篇文章讲了一点,http://dongxicheng.org/structure/trietree/
PS:关于删除某一个字符串用别的数据结构实现,应该删除起来更方便。以后研究之后继续补充。