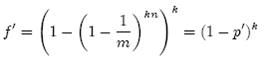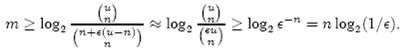Bloom Filter概念和原理 & 从哈希存储到Bloom Filter

注: Bloom Filter 系列 : http://blog.csdn.net/jiaomeng

Bloom_filter 维基http://en.wikipedia.org/wiki/Bloom_filter

guava-bloomfilter http://www.oschina.net/translate/guava-bloomfilter?cmp

Bloom Filter概念和原理

焦萌 2007年1月27日

 

Bloom Filter是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于这个集合。Bloom Filter的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

集合表示和元素查询

下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0。

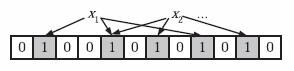
为了表达S={x₁, x₂,…,x_n}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置h_i(x)就会被置为1（1≤i≤k）。注意，如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位）。   

 

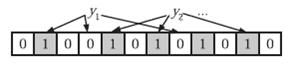
在判断y是否属于这个集合时，我们对y应用k次哈希函数，如果所有h_i(y)的位置都是1（1≤i≤k），那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y₁就不是集合中的元素。y₂或者属于这个集合，或者刚好是一个false positive。

错误率估计

前面我们已经提到了，Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率（false positive rate），下面我们就来估计错误率的大小。在估计之前为了简化模型，我们假设kn<m且各个哈希函数是完全随机的。当集合S={x₁, x₂,…,x_n}的所有元素都被k个哈希函数映射到m位的位数组中时，这个位数组中某一位还是0的概率是：

其中1/m表示任意一个哈希函数选中这一位的概率（前提是哈希函数是完全随机的），(1-1/m)表示哈希一次没有选中这一位的概率。要把S完全映射到位数组中，需要做kn次哈希。某一位还是0意味着kn次哈希都没有选中它，因此这个概率就是（1-1/m）的kn次方。令p = e^-kn/m是为了简化运算，这里用到了计算e时常用的近似：

 

令ρ为位数组中0的比例，则ρ的数学期望E(ρ)= p’。在ρ已知的情况下，要求的错误率（false positive rate）为：

(1-ρ)为位数组中1的比例，(1-ρ)^k就表示k次哈希都刚好选中1的区域，即false positive rate。上式中第二步近似在前面已经提到了，现在来看第一步近似。p’只是ρ的数学期望，在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher已经证明^[2] ，位数组中0的比例非常集中地分布在它的数学期望值的附近。因此，第一步的近似得以成立。分别将p和p’代入上式中，得：

   

   

相比p’和f’，使用p和f通常在分析中更为方便。

最优的哈希函数个数

既然Bloom Filter要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢？这里有两个互斥的理由：如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到0的概率就大；但另一方面，如果哈希函数的个数少，那么位数组中的0就多。为了得到最优的哈希函数个数，我们需要根据上一小节中的错误率公式进行计算。

 

先用p和f进行计算。注意到f = exp(k ln(1 − e^−kn/m))，我们令g = k ln(1 − e^−kn/m)，只要让g取到最小，f自然也取到最小。由于p = e^-kn/m，我们可以将g写成

根据对称性法则可以很容易看出当p = 1/2，也就是k = ln2· (m/n)时，g取得最小值。在这种情况下，最小错误率f等于(1/2)^k≈ (0.6185)^m/n。另外，注意到p是位数组中某一位仍是0的概率，所以p = 1/2对应着位数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

 

需要强调的一点是，p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 − (1 − 1/m)^kn))，g’ = k ln(1 − (1 − 1/m)^kn)，p’ = (1 − 1/m)^kn，我们可以将g’写成

同样根据对称性法则可以得到当p’ = 1/2时，g’取得最小值。

位数组的大小

下面我们来看看，在不超过一定错误率的情况下，Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素，允许的最大错误率为є，下面我们来求位数组的位数m。

 

假设X为全集中任取n个元素的集合，F(X)是表示X的位数组。那么对于集合X中任意一个元素x，在s = F(X)中查询x都能得到肯定的结果，即s能够接受x。显然，由于Bloom Filter引入了错误，s能够接受的不仅仅是X中的元素，它还能够є (u - n)个false positive。因此，对于一个确定的位数组来说，它能够接受总共n + є (u - n)个元素。在n + є (u - n)个元素中，s真正表示的只有其中n个，所以一个确定的位数组可以表示

个集合。m位的位数组共有2^m个不同的组合，进而可以推出，m位的位数组可以表示

   

个集合。全集中n个元素的集合总共有

   

个，因此要让m位的位数组能够表示所有n个元素的集合，必须有

   

即：

   

上式中的近似前提是n和єu相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于є的情况下，m至少要等于n log₂(1/є)才能表示任意n个元素的集合。

 

上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小，这时f = (1/2)^k= (1/2)^{mln2 / n}。现在令f≤є，可以推出

这个结果比前面我们算得的下界n log₂(1/є)大了log₂e≈ 1.44倍。这说明在哈希函数的个数取到最优时，要让错误率不超过є，m至少需要取到最小值的1.44倍。

总结

在计算机科学中，我们常常会碰到时间换空间或者空间换时间的情况，即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素：错误率。在使用Bloom Filter判断一个元素是否属于某个集合时，会有一定的错误率。也就是说，有可能把不属于这个集合的元素误认为属于这个集合（False Positive），但不会把属于这个集合的元素误认为不属于这个集合（False Negative）。在增加了错误率这个因素之后，Bloom Filter通过允许少量的错误来节省大量的存储空间。

 

自从Burton Bloom在70年代提出Bloom Filter之后，Bloom Filter就被广泛用于拼写检查和数据库系统中。近一二十年，伴随着网络的普及和发展，Bloom Filter在网络领域获得了新生，各种Bloom Filter变种和新的应用不断出现。可以预见，随着网络应用的不断深入，新的变种和应用将会继续出现，Bloom Filter必将获得更大的发展。

参考资料

[1] A. Broder and M. Mitzenmacher.Network applications of bloom filters: A survey. Internet Mathematics, 1(4):485–509, 2005.

[2] M. Mitzenmacher.Compressed Bloom Filters. IEEE/ACM Transactions on Networking 10:5 (2002), 604—612.

[3] www.cs.jhu.edu/~fabian/courses/CS600.624/slides/bloomslides.pdf

[4] http://166.111.248.20/seminar/2006_11_23/hash_2_yaxuan.ppt

从哈希存储到Bloom Filter

焦萌 2007年1月28日

 

先解释一下什么是哈希函数。哈希函数简单来说就是一种映射，它可取值的范围（定义域）通常很大，但值域相对较小。哈希函数所作的工作就是将一个很大定义域内的值映射到一个相对较小的值域内。

传统的哈希存储

假设要哈希的集合为S，它有n个元素。传统的哈希方法是，将哈希区域组织成h（h > n）个格子的列表，每一个格子都能存储S中的一个元素。存储时将S中的每一个元素映射到{0, 1, … , h-1}的范围内，然后以这个值为索引将此元素存储到对应的格子内。由于哈希函数将一个大集合映射到一个小集合中，所以存在将大集合中的多个元素映射到同一位置的情况，这就是所谓的碰撞（Collision）。当碰撞发生时，有多种策略可供选择，比如用链表将映射到同一位置的元素串起来，或者在碰撞发生时再进行哈希映射直到找到空位为止等等。

 

传统的哈希方法不会发生错误，而且存储的元素还可以复原。如果哈希函数选择得当，碰撞出现的情况比较少，那么查找某一个元素也很快。但是，如果你哈希某个集合只是为了判断某个元素是否在这个集合中，那么你会发现好像存储整个集合有点浪费。按传统的哈希方法判断某个元素是否属于集合时，会把这个元素和它映射位置上的元素进行匹配，如果完全匹配则说明属于集合，如果不匹配则不属于。在绝大部分查找都不能匹配的情况下（这常常是实际中的情况），我们会发现匹配的过程经常用不到整个元素，因为元素的一部分就可以判断不匹配了。基于“部分信息就能判断不匹配”这个思路，Burton Bloom（Bloom Filter的发明者）提出了一种改进的方法。

改进的哈希存储

在这种改进的方法中，哈希区域和前面一样仍然被组织成格子的列表。但这次并不直接将集合元素存在格子里，而是将每一个元素编码然后将编码存在格子里。假设每个集合元素要占b位，编码后要占c（c < b）位。由于编码位数少于元素位数，不同元素的编码有可能相同，因此在查找元素时可能会出现错误。编码位数取决于你期望的错误率：编码位数越多，错误就越少，反之则越大；当错误少到一定程度（大约2^-b），编码位数就足以存下整个元素，因此就变回了传统的哈希存储。

 

这种方法对传统的哈希存储进行了改良，允许用户在错误率和存储空间之间作权衡。这里我们已经能够看到Bloom Filter的一点端倪。如果说这种方法已经孕育了“正确率换空间”的思想的话，那么Bloom Filter更是这个思想的大胆实践，它完全摆脱了传统的哈希存储方法，在存储空间使用和减少错误率方面又进了一步。

Bloom Filter

在Bloom Filter中，哈希区域的每一位都被当成是独立的可寻址的单元。在对集合元素进行编码时，同时使用若干个独立的哈希函数，将每一个哈希函数映射的地址都置为1。这种编码方法可谓是另辟蹊径，摆脱了原来一个格子一个格子的存储方法。在改进的哈希存储中，编码位数是和正确率交换的筹码，而在Bloom Filter中，筹码变成了哈希函数的个数以及整个哈希区域（即位数组）的大小。如果想具体知道合适的哈希函数个数和位数组大小，请参阅第一篇Bloom Filter概念和原理。

 

和前面两种哈希存储方法相比，Bloom Filter最大的优势自然是它的空间效率。另外，由于Bloom Filter不用处理碰撞（Collision），因此它在增加或查找集合元素时所用的时间完全恒定（哈希函数的计算时间），无论集合元素本身有多大，也无论多少集合元素已经加入到了位数组中。由于Bloom Filter和改进的哈希存储都对集合元素进行了编码，因此想要从哈希区域中恢复集合元素并不容易。但同时，如果你不想让别人直接看到集合元素，这样的编码处理倒可以看成是一种加密，有效保护了你的隐私。

 

Bloom Filter很大的一个缺点就是不能删除元素。由于Bloom Filter不处理碰撞，有可能多个哈希函数都映射到了同一位，因此不能简单地在删除时将1置为0。后面我们会看到，Counting Bloom Filter通过将每一位扩展为一个Counter来解决这一问题。

参考资料

[1] B. Bloom. Space/Time Tradeoffs in Hash Coding with Allowable Errors. Communications of the ACM 13:7 (1970), 422—426.

[2] http://www.cs.berkeley.edu/~pbg/cs270/notes/lec27.pdf

[3] http://security.riit.tsinghua.edu.cn/seminar/2006_11_16/hash_function_yaxuan.ppt

参考：

从哈希存储到Bloom Filter http://blog.csdn.net/jiaomeng/article/details/1496329

Bloom Filter概念和原理 http://blog.csdn.net/jiaomeng/article/details/1495500

Bloom Filter 系列 : http://blog.csdn.net/jiaomeng
Bloom_filter 维基 http://en.wikipedia.org/wiki/Bloom_filter