HDOJ - 3068 最长回文 Manacher
早就听说过这个方法..当时不理解就过了...今天再来写这题..带来的感觉很深刻...
充分利用前面判断过的内容...尽可能减少重复判断是Manacher的核心....
预处理..但凡回文串的问题..在这个串的最头和最末以及每个字符中间加入相同的冗余字符..这样就可以把奇偶情况一起讨论了..记住最后结果除以2...
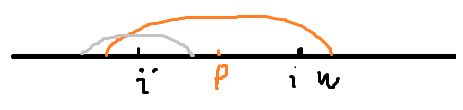
dp [ i ] 代表以 s [ i ] 为中心的回文串最长长度...dp值从字符串最左更新到最右...每次除了更新dp [ i ] 还要维护两个值...w , i ( 前面一段某点为中心的回文所能到的最右的位置 w, 以及这个中间点是哪个 p )....
充分利用回文串的特点..左右对称相等.. 看下面两种情况:
1>
当前扫到了i...之前p能到最右距离w...那么可以将i对称p找到左侧的对应点...并且这个点的回文长度在p最长回为之内..那么dp[i]=dp[2*p-i]...直接赋值....
2>
当前点i对称于p的点是i'...而i'的最长回文范围已经超过p的范围...所以只能得出..以i为中点..w为右界的回文串是ok的...但要从w+1继续往后面判断..以i为中心找到不能回文为止..此时将p改为i...w改为i的最右位置....
关于效率的问题...由于w是单调往右移动的...所以时间效率是O(n)....
Program:
#include<iostream>
#include<string>
#include<cmath>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#define ll long long
#define oo 1000000000
using namespace std;
char str[250005],s[250005];
int dp[250005];
int main()
{
int l,i,j,w,p,k,ans;
while (~scanf("%s",&str))
{
l=strlen(str);
memset(dp,0,sizeof(dp));
s[0]='*';
for (i=0;i<l;i++) s[i*2+1]=str[i],s[i*2+2]='*';
l*=2;
memset(dp,0,sizeof(dp));
dp[0]=ans=1; w=p=0;
for (i=1;i<=l;i++)
{
if (i<=w) dp[i]=dp[2*p-i];
if (i+dp[i]/2>=w)
{
p=i;
if (w>=i) dp[i]=(w-i)*2;
else w=i;
dp[i]++;
while (w+1<=l && s[w+1]==s[2*p-w-1]) dp[i]+=2,w++;
}
if (ans<dp[i]) ans=dp[i];
}
printf("%d\n",ans/2);
}
return 0;
}