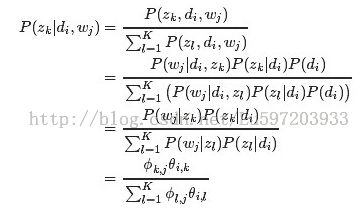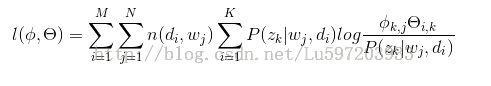概念主题模型简记
概念主题模型(PTM, probabilitytopical model)在自然语言处理(NLP,natural language processing)中有着重要的应用。主要包括以下几个模型:LSA(latentsemantic analysis)、 PLSA(probability latent semantic analysis)、LDA(latentdirichlet allocation)和HDP(hirerachical dirichlet processing),这里用一张图给出它们的发展历程。此记主要记录PLSA和LDA模型.
PLSA:
PLSA是在LSA的基础上发展起来的,因为LSA有以下缺点:(1)svd奇异值分解对数据的变化较为敏感,同时缺乏先验信息的植入等而显得过分机械。(2)缺乏稳固的数理统计基础(奇异值分解物理意义,如何从数学上推导得出高维降到的低维语义结构空间),此外svd分解比较耗时。基于以上两个原因,提出了PLSA(概率潜在语义结构分析),这样我们就从概率的角度对LSA进行新的诠释,使得LSA有了稳固的统计学基础。
PLSA不关注词和词之间的出现顺序,所以pLSA是一种词袋方法(BOW: 一个文档用一个向量表示,向量中元素就是一个词出现与否或者是出现次数或者TF-IDF,各个词是否出现相互独立),具体说来,该模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别![]() 。同时定义:
。同时定义:
- P(di)表示海量文档中某篇文档被选中的概率。
- P(wj|di)表示词wj在给定文档di中出现的概率。
- 怎么计算得到呢?针对海量文档,对所有文档进行分词后,得到一个词汇列表,这样每篇文档就是一个词语的集合。对于每个词语,用它在文档中出现的次数除以文档中词语总的数目便是它在文档中出现的概率P(wj|di)。
- P(zk|di)表示具体某个主题zk在给定文档di下出现的概率。
- P(wj|zk)表示具体某个词wj在给定主题下出现的概率zk,与主题关系越密切的词,其条件概率P(wj|zk)越大。
利用上述的第1、3、4个概率,我们便可以按照如下的步骤得到“文档-词项”的生成模型:
- 按照概率P(di)选择一篇文档di
- 选定文档di后,从主题分布中按照概率P(zk|di)选择一个隐含的主题类别zk
- 选定zk后,从词分布中按照概率P(wj|zk)选择一个词wj
这样可以根据大量已知的文档-词项信息P(wj|di),训练出文档-主题P(zk|di)和主题-词项P(wj|zk),如下公式所示:
故得到文档中每个词的生成概率为:
由于P(di)可事先计算求出,而P(wj|zk)和P(zk|di)未知,所以![]() 就是我们要估计的参数(值).由于含有隐含的主题变量z,所有我们考虑使用EM算法。
就是我们要估计的参数(值).由于含有隐含的主题变量z,所有我们考虑使用EM算法。
我们使用最大似然估计得到:
这里:n(di,wj)表示词项wj在文档di中词频,n(di)表示文档di中词的总数。M表示文档数量,N表示单词数量
其对数似然估计为:
下面用EM算法进行求解:
E-step:
M-step:
由前面的对数似然函数知:
我们去除不必要的常数项得到:
约束条件为:
这里通过largange乘数法求:
最终我们便求得参数即为每个文档中主题发生的概率及在该主题下词发生的概率,然后就
可以用得到得参数对文档或者文档中的词进行分类等。
LDA
LDA:隐含的狄利克雷分布,要了解LDA,需要一些数学基础,包括二项分布,多项式分布,beta分布,dirichlet分布.这几个分布可以参看这篇blog:http://blog.csdn.net/v_july_v/article/details/41209515,此外这篇blog:http://blog.csdn.net/lu597203933/article/details/45933719讲解MLE(最大似然估计)、MAP(最大后验概率估计)及贝叶斯估计的区别。
这里我们会得出:
参数p的先验概率为beta(或者dirichlet)分布,那么以p为参数的二项分布(或者多项式分布)通过贝叶斯估计得到的后验概率分布仍然是beta分布(或者dirichlet分布)。我们说beta分布式是二项式分布的共轭先验概率分布,而dirichlet分布为多项式分布的共轭先验概率分布。如何理解这句话呢?
我们举一个简单的例子:比如投硬币,我们将p记为正面发生的概率,这样我们投了20次,出现正面12次,反面8次。这就是所谓的样本空间X, P(X|p) = p^12*(1-p)^8是以p为参数的二项式分布。假设p有个先验分布beta(a,b)(a和b为beta分布的参数,为什么选择beta,后面讲)。现在我们用贝叶斯估计,即最大化P(p|X),通过公式推导我们会发现P(p|X)服从的也是beta分布,为beta(a+12,b+8)。如果看不懂可以再看看这篇blog:http://blog.csdn.net/lu597203933/article/details/45933719
那么现在有以下几个问题:
1:为什么选用beta分布或者dirichlet分布?
<1>beta分布+二项分布得到的仍然是beta分布,这样就给计算带来了方便,可以直接利用beta分布的均值方差公式得到结果
<2>beta分布可以通过变换不同参数得到不同形状分布的概率密度函数,通过选择参数(称为超参数)一定能满足我们的需求(形状千奇百怪,高低胖瘦)。
dirichlet分布和多项式分布分别是beta分布和二项分布在多维情况的推广!
2:为什么选择贝叶斯估计?
贝叶斯估计参数的表示方式更为精确,得到的参数也更为精确,越来越能反应基于样本的真实参数情况。没有将参数作为固定未知值,而是将其作为随机变量,先验为一个概率分布(人们已经知道或普遍接受的规律),这样就会对后续参数估计产生一定的影响。
这里给出频率学派和贝叶斯学派的区别:
频率学派:参数是未知的,但是固定,样本空间X是随机变量,最大似然估计(MLE,maximumlikehood estimation)
贝叶斯学派:参数具有一个先验概率分布(人们已经知道或者普遍接受的规律),参数可以看做是一个随机变量,不再固定,有最大后验估计(MAP,maximum a posterior)和贝叶斯估计两种方法。
LDA的过程为:
lda实质上就是plsa加了一个贝叶斯框架,过程可以描述为:由先验dirichlet分布得到主题的概率分布(P(p)),然后通过已有样本得到的主题样本空间(潜在的)服从的是以dirichlet分布概率作为参数的多项式分布(P(X|p)),这样通过贝叶斯估计得到每个主题的后验概率分布仍为dirichlet分布(P(p|X));;一个主题下的每个词先验分布也是dirichlet分布,词样本空间服从的是以dirichlet分布概率作为参数的多项式分布,这样通过贝叶斯估计得到的后验概率分布仍然为dirichlet分布。从MLE到MAP再到贝叶斯估计,对参数的表示越来越精确,越来越能够反映基于样本的真实参数情况。
举一个简单的例子,假设一篇文档 中有3个主题,根据单词统计得出主题1,2和3的概率相等都是1/3,,但是如果我们之前给这三个主题概率(p1,p2,p3)加入一个dirichlet分布(参数p1,p2,p3服从的概率分布),那么通过贝叶斯估计后三个主题的概率分别为1/2. 1/3,1/6将会更加符合真实情况。。
之所以选择dirichlet分布作为先验概率分布,因为主题和词的分布都是多项式分布,所以dirichlet先验概率分布+多项式分布得出的结果仍然是dirichlet分布,这样就可以使用dirichlet分布的性质了。
总结:plsa和lda最终需要求得的参数都是每个文档中主题发生的概率及在该主题下词发生的概率,参数即为两个矩阵,然后就可以用得到得参数对文档或者文档中的词进行分类等。只不过lda是plsa的贝叶斯化,先验概率服从dirichlet分布,贝叶斯化的好处一方面使得到的参数更加精确,另一方面贝叶斯学派的观点可以降低过拟合等优点!
此外:对lda的参数估计方法gibbs sampling算法,我还没有看,后续再补充!。欢迎有任何问题的进行交流!
这里给出一般的共轭分布表:
参考文献:
1:http://blog.csdn.net/v_july_v/article/details/41209515 通俗理解LDA主题模型
2:http://blog.csdn.net/yangliuy/article/details/8296481文本语言模型的参数估计-最大似然估计、MAP及贝叶斯估计
3:http://blog.csdn.net/yangliuy/article/details/8330640
4:http://maider.blog.sohu.com/306392863.html如何理解beta分布和dirichlet分布
5:http://vdisk.weibo.com/s/zrFL6OXKgKMAf沈博ppt
***************以下内容为最近需要用到lda学习时的笔记(2016/2/1)***************************
对于lda的dirichlet分布是多项式的共轭先验概率分布、beta分布、gamma分布、频率学派和贝叶斯学派思想的区别【注意频率学派和贝叶斯学派思想没有好坏之分,他们都是认识自然的两种手段,只是在当前人们掌握的数学工具和需要解决的数学问题中,贝叶斯学派的理论体系能够更好的解释目标函数和分析相互关系等[1]】及MLE,MAP及贝叶斯估计等这些概念性的东西都可以参看文末的参考文献[1][2]或者上面笔记给出的参看文献,这里不再详解。这里主要是讲解gibbs采样的过程及我在学习gibbs采样过程中一些令我疑惑的问题。
当然在描述gibbs采样之前,我还是给出几个公式的结果,具体推到过程就不讲了,不明白的可以看参考文献或者留言。
gibbs采样总是采用概率向量的一个维度,给定其他维度的变量值来采样当前维度的变量值,设i=(m,n)是一个二维下标,对应第m个文档中第n个单词,~i表示除去下标为i的词语。p(zm,n=k|z~i,w)表示的就是在不考虑第m个文档中第n个词的情况下,该词属于主题k(计算出属于所有主题k的概率,k范围从1到K)的概率,推导的公式如下:
此公式即被称为gibbsupdating rule ,其中第一行到第二行将p(wi)省略掉了是由于其只与当前的单词本身有关,可以看作是一个常量,常量对最终的结果不会产生任何影响,因为对于每一个主题k(1~K), 都将常量省略掉了,故只是放大缩小倍数而已。第二行到第三行采用了delta与gamma函数之间的关系推到得出。第三行到第四行采用公式3即可得出,最后两行省略掉分母是因为分母即当前第m篇文档中单词的数目-1,即为常量,常量当然可以省去。
Gibbs采样步骤为随机初始化、采样、判断收敛。其中初始化就是将每篇文档中的每个词都随机的初始化分配一个主题,然后针对第m篇文档第n个单词,,采用gibbsupdating rule对其进行重新采样,采样叠加法(后面讲解)将其归属于新的主题,然后不断迭代每个文档中的每个词,直到最终的每篇文档中的主题分布与每个主题中的词分布达到收敛或者初始设定的迭代次数。给出文献[2]中的gibbs过程
下面给出自己在学习lda过程中的一些疑惑问题及解答
1:lda不仅仅可以使用gibbs采样进行参数学习,刚开始是使用变分EM算法进行求解,这也是原论文的参数求解方式,但是变分EM算法推导复杂,此外该方法得到的往往不是全局最优解,而是局部最优解。而gibbs采样推导不难,但收敛速度慢点,但是已有相应的该进,sparselda就是提升gibbs采样速度而提出。
2:为什么说lda也是一种聚类过程。因为每篇文档最终都会得到一个主题分布,我们可以选择该文档最大的主题概率作为该文档的类别,那么就将这些文档分配到K个类别中了。——当然,如果选择最大的2个主题作为文档的标签,理论上就最终得到了K*(K-1)/2个类别。同时解释了LDA可以一定程度的认为是“聚类”
3:gibbssampling updating过程中等同于就可以了,不需要相等,依据gibbs sampling,主要计算该词属于每个主题的概率,该词针对的每个主题的计算公式中都会有该常量,因此该常量在对于将某个词分配给那个主题计算就没有影响了,只是都放大或者缩小了多少倍而已。
4:如何确定topic个数?topic太小易欠拟合,太大易过拟合。原始论文中采用的评测指标perplexity, 即针对每个主题,我们可以训练参数得到一个perplexity值,然后得到perplexity-topic分布曲线,会发现perplexity随着topic number增大不断减小直至稳定。选择稳定拐角点处的topic number作为该训练数据的topic number(perplexity可以用来验证模型的好坏和结果是否已经收敛) 另外还有一个指标就是MPI(point-wise mutualinformation)[7], 此外文献[7]同时给出当k过大过拟合时,模型性能可能会严重退化
注:确定topic的数目没有好的办法,只能用交叉验证,而hdp比较复杂,更多的存在于学术上
5:超参数的选择:采用对称dirichlet分布的原因是表明每个主题都会有相同的概率被分配到一个文档中,每个单词有相同的概率被分配到同一个主题(因为没有任何先验信息)。一般alpha和beta都采用小于1的值(因为这样其概率密度曲线变得比较稀疏) ;启发式的alpha=1/topic number, beta=0.01。alpha表明了不同文档间主题是否鲜明,beta表明有多少个近义词能属于同一类别。。实际中给定了topic number,对alpha和beta进行训练能显著改善模型的效果。
文献[8]给出超参数alpha取非对称值占据足够的优势,而beta取非对称值则没有好处
6:lda的应用:相似文档,自动打标签,推荐系统,topic rank,word rank等—详细见lda漫游指南[6]
7:文献[7]获得了2014 ICML best paper,分析了文档数目,文档长度及超参数对lda模型的影响及学习建议,值得一读。
8:(累加法):当为某个词sample一个新的主题时,计算是这样的,首先得到某个词属于各个主题的概率,并不是取最大的,而是看落在那个累积概率中。是这样理解,在轮盘赌中,某一分区面积越大,指针落到该区域概率越大,这里取得是累积概率就好比是轮盘的某个区域的面积,区域的label就是topic index 。比如3个主题的概率为[0.3,0.1,0.6], 累计概率为[0.3,0.4,1], 那么随机采样值为0.35,由于0.35落在0.4区域中,因此此时选择的主题是2而不是3.—不太懂(有深入理解的请指教)
9: 文档数量也会严重影响模型的性能,当文档数量较少时,即使每篇文档非常长,也不可能达到较好的效果,一般都要有足够的文档数量,或者从大批量的预料库中随机选择上千的文档也是可以的[7]
10:每篇文档长度对模型性能起着关键的作用,当文档很短,即使有非常多数量的文档,模型也不可能达到较好的效果, 文档要足够长,但是无需过长(文献[7]在实验中文档长度在120+就会收敛),对于过长的文档,可以从中采样一部分构成文档[7]。
参考文献:[详细了解可以按顺序阅读]
1:lda数学八卦
2:Parameter estimation fortext analysis 论文 GregorHeinrich 2004
3:Distributed GibbsSampling of Latent Topic Models: The Gritty Details wangyi 公式详细推导过程
4:邹博主题模型课件http://ask.julyedu.com/article/295
5:网友blog: http://blog.csdn.net/yangliuy/article/details/8302599可以看java代码了解过程
6:lda漫游指南-特别是第四章的应用http://yuedu.baidu.com/ebook/d0b441a8ccbff121dd36839a.html
7:Understanding theLimiting Factors of Topic Modeling via Posterior Contraction Analysis:2014 ICMLbest paper
8Rethinking LDA: Why Priors Matter