BNUOJ 4067 美丽的花环 (几何题)
美丽的花环
Time Limit: 1000ms Memory Limit: 65536KB
Special Judge
64-bit integer IO format:
%lld Java class name:
Main
学校的草坪上最近种植了一些漂亮的花卉,所有的花围成了一个环形(内径为r,外径为R,0 <r < R) 。原来这片地上有一个用于喷灌的喷头。这个喷头可以为半径K以内的植物提供水。(如图)
现在,HK请你帮忙计算一下,花构成的环形当中有多大面积的可以由喷头提供灌溉。
Input
输入数据只有两行。
格式为(中间使用空格隔开)
x1 y1 R r
x2 y2 K
花环中心在(x1,y1) ,外径为R,内径为r。
喷头的位置为(x2,y2),覆盖范围为K。
其中,x1,y1,R,r,x2,y2,K均为实数。
Output
输出题目描述中所求面积(保留2位小数)。
Sample Input
5 5 20 10 2 2 20
Sample Output
773.09
Hint
π的值请取:3.1415926或acos(-1.0)
分析:由图可以看出所求面积等于外环构成的圆和喷头构成的圆的相交面积减去内环构成的圆与喷头构成的圆的相交面积之差,所以问题转化成了求两个圆的相交面积。
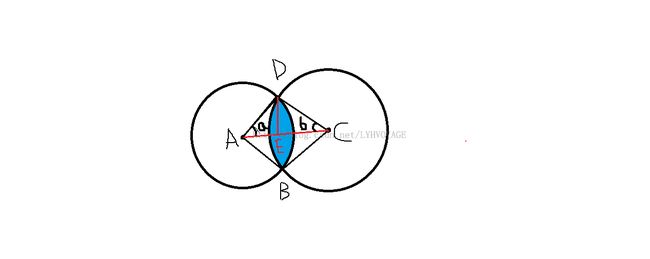
如上图。相交面积等于阴影部分的面积。通过分析不难得出,阴影部分的面积 = 扇形ADB的面积 + 扇形CDB的面积 - 四边形ABCD的面积,而这几部分的面积很容易就能求出来。具体的请参考代码部分。
#include<cstdio>
#include<cmath>
#define pi acos(-1.0)
double get_dis(double x1, double y1, double x2, double y2)
{
return sqrt((x1-x2) * (x1 - x2) + (y1-y2) * (y1-y2));
}
double get_ans(double x1, double y1, double r1, double x2, double y2, double r2)
{
double dis = get_dis(x1, y1, x2, y2);
if(dis >= r1 + r2) return 0; //圆心距大于等于半径和,两圆相交面积为0
double min_r = r1 < r2 ? r1 : r2;
double max_r = r1 > r2 ? r1 : r2;
if(min_r + dis <= max_r)
return pi * min_r * min_r; //圆心距小于半径之差,两圆包含关系
double a = acos((r1*r1 + dis*dis - r2*r2)/2/r1/dis);
double b = acos((r2*r2 + dis*dis - r1*r1)/2/r2/dis);
double area1 = a * r1 * r1; //第一个圆中扇形的面积,弧长l = a * r1, 面积等于0.5*l*r1
double area2 = b * r2 * r2; //第二个圆中扇形的面积
double ans = area1 + area2; //两个扇形的面积和等于四边形的面积加上两圆相交的面积
double area_qua = sin(a) * r1 * dis; //四边形的面积
ans -= area_qua;
return ans;
}
int main()
{
double x1, y1, R, r, x2, y2, k;
while(~scanf("%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&R,&r,&x2,&y2,&k))
{
double s1 = get_ans(x1, y1, R, x2, y2, k);
double s2 = get_ans(x1, y1, r, x2, y2, k);
printf("%.2lf\n",s1-s2);
}
return 0;
}