poj 1363 Rails （栈的应用+STL）

Rails

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 24762		Accepted: 9715

Description

There is a famous railway station in PopPush City. Country there is incredibly hilly. The station was built in last century. Unfortunately, funds were extremely limited that time. It was possible to establish only a surface track. Moreover, it turned out that the station could be only a dead-end one (see picture) and due to lack of available space it could have only one track. 

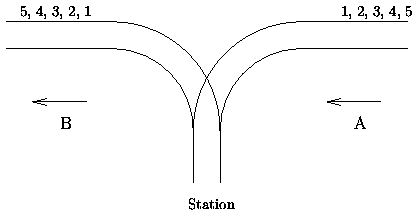
The local tradition is that every train arriving from the direction A continues in the direction B with coaches reorganized in some way. Assume that the train arriving from the direction A has N <= 1000 coaches numbered in increasing order 1, 2, ..., N. The chief for train reorganizations must know whether it is possible to marshal coaches continuing in the direction B so that their order will be a1, a2, ..., aN. Help him and write a program that decides whether it is possible to get the required order of coaches. You can assume that single coaches can be disconnected from the train before they enter the station and that they can move themselves until they are on the track in the direction B. You can also suppose that at any time there can be located as many coaches as necessary in the station. But once a coach has entered the station it cannot return to the track in the direction A and also once it has left the station in the direction B it cannot return back to the station. 

Input

The input consists of blocks of lines. Each block except the last describes one train and possibly more requirements for its reorganization. In the first line of the block there is the integer N described above. In each of the next lines of the block there is a permutation of 1, 2, ..., N. The last line of the block contains just 0. 

The last block consists of just one line containing 0.

Output

The output contains the lines corresponding to the lines with permutations in the input. A line of the output contains Yes if it is possible to marshal the coaches in the order required on the corresponding line of the input. Otherwise it contains No. In addition, there is one empty line after the lines corresponding to one block of the input. There is no line in the output corresponding to the last ``null'' block of the input.

Sample Input

5
1 2 3 4 5
5 4 1 2 3
0
6
6 5 4 3 2 1
0
0

Sample Output

Yes
No

Yes

Source

Central Europe 1997

栈的应用的简单题；就是给你一个出栈的序列，判断这段序列是否合法，这道题有两种思路：

1.每个已出栈之后的数且小于此数的数都必须按降序排列。复杂度O(n^2)，任何元素x出栈前，所有大于x的元素必须出栈，栈内的元素值必须小于x，因为大于x的元素后于x入栈，小于x的值先于x入栈；

2.直接模拟入栈出栈的过程，可以用数组模拟，也可以用STL，我这里把两种模拟都实现了；复杂度O(n)。

直接用数组模拟:用数组模拟栈

#include <cstdio>
using namespace std;
const int maxn=1000+5;
int a[maxn],b[maxn];//a数组储存入栈的序列，b数组存储要判断的序列
int main()
{
    int n,i,j,k;
    while(scanf("%d",&n)&&n)
    {
        while(scanf("%d",&b[0])&&b[0])
        {
            for(i=1;i<n;i++)
                scanf("%d",&b[i]);
           for(i=1,j=0,k=0;i<=n&&j<n;i++,j++)
           {
               a[j]=i;
               while(a[j]==b[k])//进行判断（出栈的顺序是否合理）
               {
                   if(j>0) j--;//判断下一个
                   else
                   {
                       a[j]=0;
                       j--;
                   }
                   k++;
                   if(j==-1) break;
               }
           }
           if(k==n) printf("Yes\n");//如果全部匹配就输出yes
           else printf("No\n");
        }
        printf("\n");
    }
    return 0;
}

用STL栈来实现，思想上是一样的：代码略有不同

#include <cstdio>
#include <stack>
using namespace std;
const int maxn=1000+5;
int a[maxn];
int main()
{
    int n,i,k;
    while(scanf("%d",&n)&&n)
    {
        stack<int>s;//设立一个栈储存按顺序进栈的序列 （一个空栈）
        while(scanf("%d",&a[0])&&a[0])
        {
            for(i=1;i<n;i++)
                scanf("%d",&a[i]);//要进行判断出栈的序列
            for(i=1,k=0;i<=n;i++)
            {
                s.push(i);//进栈
                while(s.top()==a[k])//判断栈顶元素和a数组是否相等
                {
                    if(!s.empty()) s.pop();//栈不为空就出栈
                    k++;//判断下一个位置
                    if(s.empty()) break;//直到栈空就结束循环
                }
            }
            if(k==n) printf("Yes\n");//完全匹配就输出yes
           else printf("No\n");
        }
        printf("\n");
    }
    return 0;
}

栈的基本思想的实现，水题，主要要掌握这种思想。