压缩感知测量矩阵之如何评价一个测量矩阵的好坏？

题目：压缩感知测量矩阵之如何评价一个测量矩阵的好坏？

一、引入

        前面的《压缩感知的常见测量矩阵》中已经给出了常见测量矩阵的MATLAB代码，似乎到此测量矩阵学习可以告一段落了，但若是专业研究压缩感知测量矩阵设计的童鞋们经常会遇到这样一个问题：我辛辛苦苦地设计了一个新型测量矩阵，那么如何证明我设计的矩阵比平常的诸如高斯矩阵、伯努利矩阵等要更好呢？

        这就是测量矩阵的评价问题，凡是做研究写论文的人，论文前面部分一般从RIP或spark角度下手去证明自己的矩阵可以作为压缩感知测量矩阵，但在论文最后一部分一般还会通过某种评价方法仿真验证自己的矩阵要优于别人的矩阵，只有这样一篇论文才感觉是完整的。

        那么如何去评价一个测量矩阵的好坏呢？

        在前面的《压缩感知测量矩阵之有限等距常数RIC的计算》中给出了一种计算RIC的MATLAB程序，但后面也提到这是一个组合复杂度的程序，现实中并不实用，只能是在理论上让大家理解一下RIC的概念；在《压缩感知的常见测量矩阵》也提到文中给出的七种测量矩阵的代码的正确性并没有验证，因为目前还没有一个简单有效的测量矩阵评价方法。

下面首先给出一些参考文献中的评价方法，然后给出自己的一些思考和疑问，为后续深入研究打下基础。

二、文献中的评价方法

        文献[1]在文中第2部分提到了RIP（定义1）、列相干性（定义2）、累积相干性函数（定义3）、零空间特性（定义3紧跟着的下一段）等来衡量测量矩阵的性能。然后文中第9部分又重新总结了矩阵的性能评价方法，包括RIP、列相干性、构造计算复杂度、矩阵维数、重构性能，并在给出了一个表格总结了文中所述矩阵的性能：

        文献[2]在文中第2.2节提到了RIP理论、相关性判别理论（传感矩阵的互相关系数）、spark判别理论、零空间理论、k-neighborly理论等，如图所示：

        文献[3]中首先从理论上推导了所构建测量矩阵的一个spark值下界（这个值与文中仿真结果相差很大，所以spark值理论推导过程值得商榷），然后在文中第3部分实验仿真及分析中，针对无噪声信号采用对比不同稀疏度下精确重建的概率，针对有噪声信号采用对比同等条件下的输出信噪比（所谓同等条件是指在满足无噪声条件下，所有被比较测量矩阵测量后均能以概率1重建），重构算法均选为OMP和BP两种，重建次数为5000次。通过对比发现，文中所设计测量矩阵针对不同的稀疏度k的无噪声信号的重建概率均高于高斯随机矩阵，针对不同的输入噪声的有噪信号输出信噪比均略高于高斯随机矩阵。

        文献[4]中可以认为并没有提出新的测量矩阵，文中通过推导认为将测量矩阵二值化后可能会提升其性能。为了验证这种思想，文中第3部分以稀疏带状随机矩阵、稀疏列随机矩阵、托普利兹矩阵为研究对象，通过仿真比较其二值化前后的恢复性能对比：选择信号长度为N=100，信号稀疏度K=20，恢复算法为OMP算法（文中对于二值化的推导基于OMP算法），测量次数M=0~100，针对每个测量次数均重构10000次，求重构概率，最终画出测量次数与重建概率的关系曲线。通过对比发现，二值化后的重建概率比原先矩阵的重建概率要高，在对比时，加入了伯努利矩阵，并且文中说“一般来说性能最优的伯努利矩阵”，矩阵二值化后的性能都接近于伯努利矩阵（以说明最优性）。（有关此文中的方法我在这里提一个疑问：对于一个由服从高斯分布的元素组成的矩阵，若以均值为界进行二值化，那么得到的矩阵不就是伯努利矩阵么？这里假定矩阵元素均非零。比如若特殊为正态分布，则均值为零，二值化就是指大于均值零的元素置为1，小于均值零的元素置为－1，根据正态分布概率密度曲线我们知道，大于零的概率为0.5小于零的概率也0.5，这不正好是一个伯努利矩阵么？）

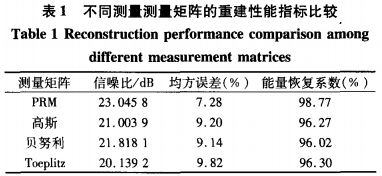
        文献[5]中第1部分提到测量矩阵的应用目标可用4条原则表示：(1)接近最佳感知性能；(2)普适性；(3)低计算复杂度；(4)便于硬件实现。然后文中构造了一种PRM测量矩阵，为了验证其性能，在文中第4部分采用二维lena标准图像和英国国家物理实验室(NPL)电能质量波形库中的一维电能质量信号进行压缩采样与重建，并给出与高斯随机矩阵、伯努利矩阵、托普利兹矩阵的性能对比结果，其中重建性能指标采用信噪比(SNR)、均方误差(MSE)、能量恢复系数(ERP)，给出的对比结果包括以表格给出的重建性能指标比较和以图形给出的压缩采样比(CSR)与输出信噪比关系曲线（CSR与文献[4]中的测量次数意义实际相同，CSR只是将测量次数相对于信号长度进行了归一化），电能质量信号的对比结果如图所示：

所有实验数据都是100次实验数据的平均结果，重构算法没说明确说明。

        文献[6]从文章题目就可以看出应该是从理论分析RIP的，在论文中，引入盖尔(Gersgorin)圆盘定理及一些其它有关高斯序列概率分布的定理，从理论上求出了准托普利兹矩阵满足RIP的概率。其实个人感觉文章到这里已经完成了论文题目的的内容，但作者在第3部分还是通过仿真比较了高斯随机矩阵、托普利兹矩阵和本文的准托普利兹矩阵三者的性能，给出了测量数-重构成功率的曲线图：

仿真实验中，信号为长度为1000点的稀疏向量，稀疏度共有40、70和120三种情况，测量数在0~400递增，对于每种测量数重复实验200次，重构算法为OMP。

        文献[7]的作者与文献[6]应该来自一个课题组，有关稀疏随机矩阵的RIP分析与文献[6]类似，还是引入盖尔(Gersgorin)圆盘定理及一些其它有关高斯序列概率分布的定理，从理论上求出了稀疏随机矩阵满足RIP的概率（无论是稀疏随机矩阵也好还是准托普利兹矩阵也罢，它们的元素都选为服从高斯分布的数）。在进行完大量的证明之后，在文中第5部分首先以一个长度为500稀疏度为30的信号为研究对象，测量次数选为200，采用OMP重构算法，仿真验证了四种不同稀疏率的稀疏随机矩阵能够精确重构出原始信号。后面又以长度为500稀疏度为50的信号为研究对象，给出了测量次数从90次到180次和重构成功率的关系曲线图；以长度为500测量值个数为200，给出了信号稀疏度从30到120和重构成功率的关系曲线图。每组参数重复实验均为1000次。不同的是，这篇文章里还给出了测量时间与矩阵稀疏率、重建时间与矩阵稀疏率的关系曲线。然后得出结论：对稀疏随机矩阵加入大量零元素，可在略微增加精确重建所需的测量值个数的情况下，大大减少测量和重建时间，对于图像压缩传感、传感器网络数据等实际应用具有重要意义。

        文献[8]构造了一种确定性随机矩阵，然后通过证明其属于亚高斯矩阵，而亚高斯矩阵满足RIP，所以文中构造的确定性随机矩阵满足RIP。然后文中第4部分做了四个实验来验证所设计矩阵的性能。实验一是在保证精确重构的前提下给出了观测向量长度M与稀疏度k之间的关系（这个与前面不同，前面好几个都是分别画出重构概率与观测向量长度M的关系曲线、重构概率与稀疏度k的关系曲线），实验重复500次；实验二给出了信号长度N为256、观测次数M为128时信号稀疏度k与重构成功率的关系曲线，实验重复500次；实验三只针对本文的矩阵的；实验四采用语音信号为研究对象，给出了压缩比与平均信噪比(SNR)、基于感知的语音质量评价方法(PESQ)的关系表格，稀疏矩阵为DCT基、重构算法为OMP。本文第5部分最后还总结了提出矩阵相比于随机观测矩阵的优点：确定性随机矩阵的元素可以通过数学运算得到，方便硬件实现；另外，产生确定性随机序列的系统方程和参数一旦确定，矩阵的元素也随之确定，在对矩阵进行传输和存储时仅需传输或存储系统方程和参数，可以提高传输效率，减小存储空间；与基于多项式的和基于代数曲线的确定性矩阵相比，确定随机矩阵的大小可以任意设置。

三、评价方法汇总

        综合以上八篇参考文献，我们可以得出常见的测量矩阵评价方法：

        (1)RIP，这个很多文献中都从理论上进行了推导证明。

        (2)测量数与重构成功率关系曲线。注意测量数即指测量矩阵的行数(M*N)，文中有多种称呼，包括测量数、测量次数、观测向量长度等。

        (3)稀疏度与重构成功率关系曲线。

        (4)对于有噪信号，常采用输出信噪比来衡量，自变量一般采用压缩比(即M/N)。

四、思考与疑问

        (1)RIP性质验证及spark常数的计算都属组合复杂度问题，目前没有什么好的办法很快计算出来。其实压缩感知的信号重构问题也是一个组合复杂度问题，但各位技术工作者们提出了各种算法，那么对于测量矩阵的评价是否也有行之有效的方法呢？也就是说设计一个测量矩阵，能否很快验证它能够满足的信号稀疏度最大是多少？

        (2)很多文献中都用重构概率曲线来说明自己的测量矩阵要优于其它测量矩阵。一般在仿真中都是采用相同的信号、稀疏矩阵、重构算法，只有测量矩阵不同，重复运行几百次或几千次，得到重构概率，以期能够说明自己的测量矩阵更优；但是这里面有个问题，对于某特定一类信号或稀疏矩阵或重构算法，它们是不是对最优测量矩阵有某种倾向性，也就是说如果换一类信号或稀疏矩阵或重构算法，重构概率仿真的结果会不会与之前是不同的？会不会原先重构概率最高的测量矩阵在换一类信号或稀疏矩阵或重构算法之后其重构概率就变得比其它测量矩阵低了？两个不同公斤级的举重选手按同一标准比赛实际上是不公平的。

        之所以会有第(2)个疑问，这是由于很多文献中都提出了一种性能很好的矩阵，因为文中的确通过仿真可以证明所设计的矩阵的确优于其它矩阵，但真的是这样子么？在不同的场景下（比如信号不同、稀疏矩阵不同、重构算法不同）还能重现这种优越性么？

        (3)对于各种文献的仿真结果，如果审稿人提这么一个意见的话应该怎么回答：仿真次数为什么选择100次[5]、200次[6]、500次[8]、1000次[7]、5000次[3]、10000次[4]？

五、结语

        测量矩阵到此就告一段落了，后续将学习研究重构算法和应用。有几个疑问放在这里：

        (1)对于M×N的测量矩阵，一般综述性文献中都会注明M<<N，但我们会发现好多文献中M都很接近于N，我一直在想压缩感知后面的重构算法比普通奈奎斯特采样定理的信号恢复要复杂不知道多少倍，换来的却是不太大的压缩率，这值得么？

        (2)一般在压缩感知文献中信号都是N维的离散信号，而我们一直在夸赞的压缩感知的优点是边压缩边采样，当然，可以在压缩感知理论框架下设计模拟信息转换器(AIC)，在前面的《压缩感知与Nquist抽样定理——模拟信息转换(AIC)学习总结》中提到的第三种基于随机解调的AIC，个人认为是真正基于压缩感知理论框架下的模拟信息转换器，由于面向的是模拟信号，所以稀疏基的元素也是连续的（但系数是离散的），我们经过推导最后得到的是传感矩阵A=ΦΨ的元素表达式，那么我的疑问是那么多文献中都设计了自己的测量矩阵，它们能实用到AIC中么？如果压缩感知脱离了“边压缩边采样”，它的实际意义在哪里？

 

【参考文献】

[1]王强，李佳，沈毅.压缩感知中确定性测量矩阵构造算法综述[J]. 电子学报，2013，41(10)：2041-2050.

[2]焦李成，杨淑媛，刘芳，侯彪. 压缩感知回顾与展望[J]. 电子学报，2011，39(7)：1651-1662.

[3]党骙，马林华，田雨，张海威，茹乐，李小蓓. m序列压缩感知测量矩阵构造[J]. 西安电子科技大学（自然科学版），2015，42(2)：215-222.

[4]朱志臻，周崇彬，刘发林，李滨兵，张志达. 用于压缩感知的二值化测量矩阵[J]. 微波学报，2014，30(2)：79-83，96.

[5]王学伟，崔广伟，王琳，贾晓璐，聂伟.基于平衡Gold序列的压缩感知测量矩阵的构造[J]. 仪器仪表学报，2014，35(1)：97-102.

[6]王开，刘郁林，和继威.准Toeplitz测量矩阵的有限等距性质分析[J].计算机应用研究，2011，28(4)：1512-1514.

[7]张波，刘郁林，王开.稀疏随机矩阵有限等矩性质分析[J]. 电子与信息学报，2014，36(1)：169-174.

[8]王侠，王开，王青云，梁瑞宇，左加阔，赵力，邹采荣. 压缩感知中的确定性随机观测矩阵构造[J]. 信号处理，2014，30(4)：436-442.