Introduction to B-Spline Curve

Introduction to B-Spline Curve

 

BSpline基函数

BSpline基函数是由下面的公式定义的:

 

 

 

 

其中 称为knot，一条BSpline曲线的所有kont组成了一个数组 ，这个数组U称为knot vector。这个公式看起来很复杂，但是慢慢分析这个公式，就可很容易的记忆它。下面，我们来分析一下这个公式。

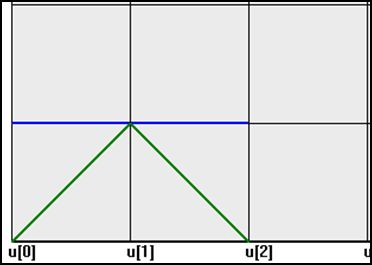
来看看零次第i项BSpline基函数的图形，很简单，它就是一条在 区间内的直线段。

 

 

 

 

因为p=0，i=0的时候，通过公式 ，在u[0]和u[1]之间就是一条直线，上图中用蓝色表示出来了。注意u[1]的值不等于1。再来看看一次第i项BSpline基函数的图形。

 

  

 

上图中，蓝色直线段分别是零次第1项BSpline基函数和零次第二项BSpline基函数，绿色的是1次第1项BSpline基函数。可以看出1次曲线是0次曲线通过线性组合得到的。因为根据公式

 

 

 

 

我们得到

 

现在把上面的等式替换为

 

其中 ，当u确定的时候， 都是常数。在u[0]和u[1]之间， 表示u点在区间u[0]和u[1]上的比例。在u[1]和u[2]之间， 表示u点在区间u[1]和u[2]上的比例。如果把 看成一条直线，u在这里是变量，那么直线 和上图中u[1]和u[2]间的蓝色直线段合成为左半绿色的直线段。同理， 就和上图中u[1]和u[2]间的蓝色直线段和成为右半绿色的直线段。下面来看看更高次的情况。下图是二次第1项BSpline基函数的图形。

 

 

 

 

同样地，上图中红色的二次曲线就是由二条绿色一次曲线合成的。如果展开公式，我们可以得到

 

 

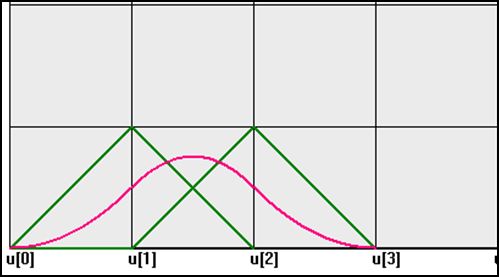
下面来看一个例子，令U={0,1,2,3,4,5}，写出所有2次BSpline基函数。

 

 

同理可以计算，通过计算，最后就得到了在 U={0,1,2,3,4,5}上所有2次BSpline基函数，如下图。

 

 

  

现在给出BSpline基函数的性质。

1.     是阶梯函数。

 

2.     当P>0， 是P-1次BSpline函数的线性组合。

 

3.     计算基函数时，必须知道knot vector U和次数P。

 

4.     是分段多项式。

 

5.     半开区间 的长度可以是0，这时 。

 

6.     如果U={0，…，0，1，…，1}，这里有p+1个0，和p+1个1，p是曲线次数，那么 表示p次Berstein基函数。这个性质说明Bezier曲线是BSpline曲线的特殊情况，并且Bezier和BSpline曲线可以相互转换。

 

7.

          。

 

8.

         。

 

9.     在knot， 有着p-k次连续性，这里k是knot重复的次数。

 

BSpline曲线

有了前面BSpline基函数的定义，现在就可以定义BSpline了。BSpline的定义和Bezier曲线的定义很相似。

 

这里 是控制点， 是上一节定义的基函数。要注意的是，p次BSpline曲线的knot区间是0到m，

这里m=p+n+1， n是最后一个控制点索引号，即 。比如下面3次BSpline曲线，它有6个控制点，m=9。

 

  

 

图中绿色的点就是控制点。对于Bezier曲线来说，它的控制点决定了曲线的次数，当控制点增多时，曲线的次数也会增加。比如一个有10个控制点的Bezier曲线，它的次数达到了9次，这在计算上很耗时间。次数越高，曲线摆动也就越厉害，也就越难控制。所以一般都用细分Bezier曲线的方式，将一个高次的Bezier曲线分成几段相连接的低次Bezier曲线，但是要注意连接点的连续性，至少要到达 连续才行。而BSpline曲线的好处就是低次曲线也可以有很多控制点，在连接点处本身就到达了 连续。

上面的BSpline曲线中，2个端点并在控制点上，这点看起来和Bezier曲线有很多差别。但是，如果我们把knot作下调整，就可以让曲线的端点和控制点重合，这就是终点差值。如果一条BSpline曲线的次数是p， ，前面有p+1个0，后面有p+1个1，那么就可以让曲线端点和2个端点控制点重合。

 

 

 *原创文章，转载请注明出处*