AA树
在上一篇博客中写道红黑树的各种操作,但是它的各种操作,尤其是删除操作分类情况比较多且复杂,不容易编程实现。
因此,Arne Andersson在93年时,在一篇“Balanced search trees made simple”就对这个RBT进行了改进。但是,现在好像应用不是很多。对于这方面介绍的资料也比较少。
我写这篇文章就是想介绍一下AA树以及它的基本操作。
1、AA-Tree提出的原因:
RBT编程实现比较繁琐,因为分情况考虑比较多且复杂,为了简化红黑树而提出来的。
2、AA-Tree的定义:
1、AA-Tree是RB-Tree的一种变型,是红黑树
2、“红”结点只能作为结点的右孩子,“黑”结点均可;
3、结点中的level相当于RBT中的结点的黑高度;
4、“红”结点的level与其父结点的level相同;
5、“黑”结点的level比其父结点的level小1;
6、左孩子的level比父结点小1,右孩子的level比父结点小0或1;
注:level为1的结点不一定为叶子;
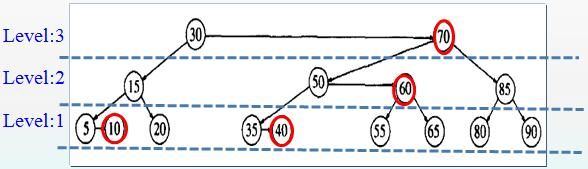
如下图所示:
3、AA-Tree的两个基本操作:
AA-Tree在插入是也只能插入“红结点”,即只能水平方向插入;但是这时会出现2中禁止出现的情况。
禁止出现的2中情况:
1、出现连续向右的水平方向链,即在RB-Tree中不能出现连续2个红结点;
2、出现向左的水平方向链,这是AA-Tree中规定的;
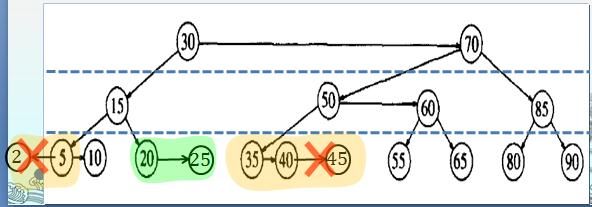
如下图所示:插入25属于正常情况,但是插入2和45是不允许出现的。
由于以上2种情况不允许出现,作者就提出AA-Tree的2个基本操作来解决上面不允许的情况。
case1:出现连续向右的水平方向链:
操作:左旋;
中间结点level加1.
如下图所示:
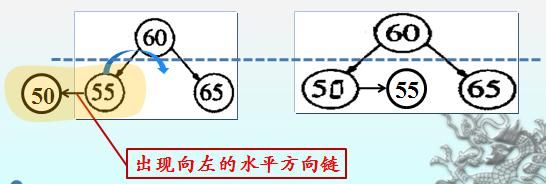
case2:出现向左的水平方向链:
操作:右旋;
如果出现向左的水平方向链,再左旋。
如下图所示:
4、AA-Tree的插入操作:
上节说到,每次插入红结点;
插入操作按照插入位置情况分类:
1、当插入结点作为其父亲的左孩子
操作:右旋;
如果出现连续水平向右的方向链,再左旋。
举例:
如下图所示: 插入 50
2、当插入结点作为其父亲的右孩子,且插入结点的父亲和祖父的level相同
操作:左旋
如果出现向左的水平链,再右旋
举例:
如下图所示,例如插入13
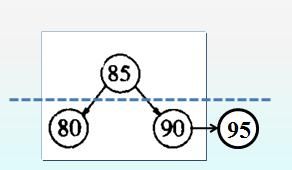
3、当插入结点作为其父亲的右孩子,且插入结点的父亲和祖父的level不同
操作:直接插入即可
举例:
如下图所示:插入 95
5、AA-Tree的删除操作:
删除操作按照后继结点是否为叶子进行分类
case1、后继结点不是叶子
操作:
后继结点的值赋给被删结点
后继结点右孩子的值赋给后继结点
删除后继的右孩子
举例:
如下图所示: 例如删除 30 ,实际上,是把40所在位置删除即可
删除后效果图,如下所示:
case2、后继结点是叶子
操作:后继结点的值赋给被删结点;
后继结点父亲的level减1;
如果出现向左或连续向右的水平链,进行右旋或者左旋;
删除后继结点。
举例:
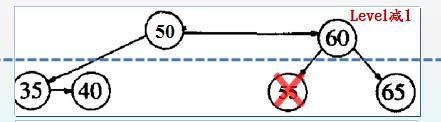
如下图所示:例如删除 50
删除后效果图,如下所示:
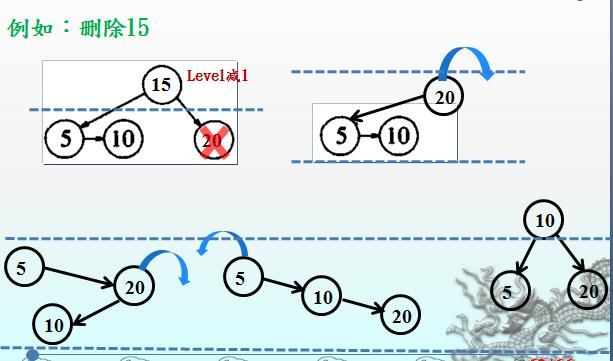
再如下图所示:删除 15
6、AA-Tree的性能分析比较
从实现角度看,AA-Tree减少了红黑树插入删除考虑的情况;
AA-Tree是BST,时间复杂度和RBT一样,即O(lgn),但是旋转次数相对较多;
7、参考文献
http://blog.csdn.net/ljsspace/article/details/6547450;
http://user.it.uu.se/~arnea/abs/simp.html