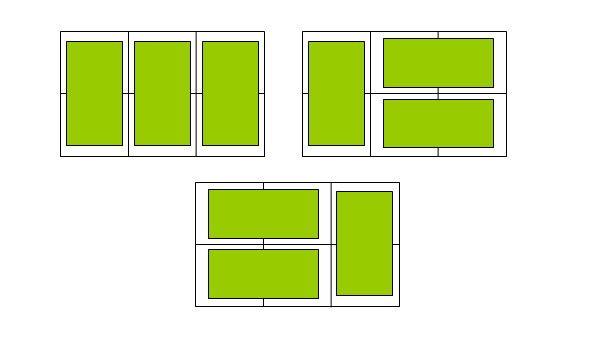
杭电OJ——2046 骨牌铺方格（简单的推断题）

骨牌铺方格

Problem Description

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

 

Input

输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。

 

Output

对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

 

Sample Input

   
   
   
   

    
    
    
    1
3
2
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    1
3
2
   
   
   
   

 

Author

lcy

 

Source

递推求解专题练习（For Beginner）

 

Recommend

lcy

 

   只要简单的推断即可~

   假设用arr[i]表示2*i的方格一共有组成的方法数，我们知道arr[1]=1;arr[2]=2;

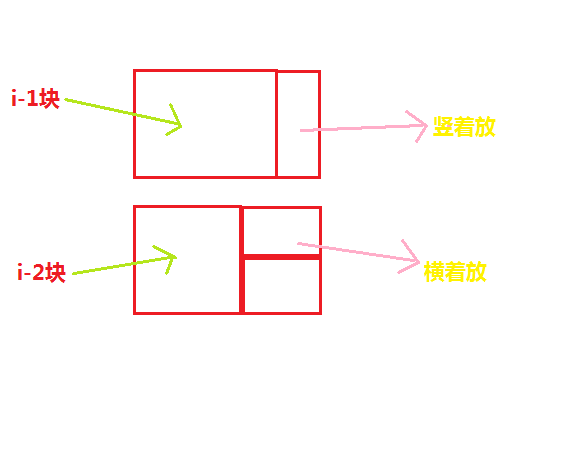
   现在假设我们已经知道了arr[i-1]和arr[i-2],求arr[i],所谓arr[i],不过是在2*（i-1）的格子后边加上一格2*1的方格罢了，骨牌在这一格上横着放，竖着放，如果前面i-1块已经铺好，则第i块只有一种铺法，就是竖着放，如果要横着放，也只有一种铺法，不过要求前面i-2块已经铺好！

 因此arr[i]=arr[i-1]+arr[i-2];

   还有数字可能会很大，用64位，我32位的交了几次都没有通过！

#include<iostream>
using namespace std;

int main()
{
	__int64 arr[51];
	int num;
	arr[1]=1;arr[2]=2;
	for(int i=3;i<=50;i++)
		arr[i]=arr[i-1]+arr[i-2];
	while(scanf("%d",&num)!=EOF)
	{
		printf("%I64d\n",arr[num]);
	}
	return 0;
}