HDU 5379 Mahjong tree(dfs)——多校练习7

Mahjong tree

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Problem Description

Little sun is an artist. Today he is playing mahjong alone. He suddenly feels that the tree in the yard doesn't look good. So he wants to decorate the tree.（The tree has n vertexs, indexed from 1 to n.）
Thought for a long time, finally he decides to use the mahjong to decorate the tree.
His mahjong is strange because all of the mahjong tiles had a distinct index.（Little sun has only n mahjong tiles, and the mahjong tiles indexed from 1 to n.）
He put the mahjong tiles on the vertexs of the tree.
As is known to all, little sun is an artist. So he want to decorate the tree as beautiful as possible.
His decoration rules are as follows:

(1)Place exact one mahjong tile on each vertex.
(2)The mahjong tiles' index must be continues which are placed on the son vertexs of a vertex.
(3)The mahjong tiles' index must be continues which are placed on the vertexs of any subtrees.

Now he want to know that he can obtain how many different beautiful mahjong tree using these rules, because of the answer can be very large, you need output the answer modulo 1e9 + 7.

 

Input

The first line of the input is a single integer T, indicates the number of test cases. 
For each test case, the first line contains an integers n. (1 <= n <= 100000)
And the next n - 1 lines, each line contains two integers ui and vi, which describes an edge of the tree, and vertex 1 is the root of the tree.

 

Output

For each test case, output one line. The output format is "Case #x: ans"(without quotes), x is the case number, starting from 1.

 

Sample Input

   
   
   
   

    
    
    
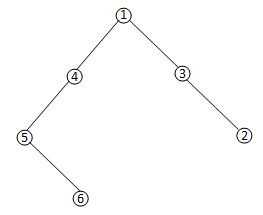
    2
9
2 1
3 1
4 3
5 3
6 2
7 4
8 7
9 3
8
2 1
3 1
4 3
5 1
6 4
7 5
8 4
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Case #1: 32
Case #2: 16
   
   
   
   

 

Source

2015 Multi-University Training Contest 7

 

/*********************************************************************/

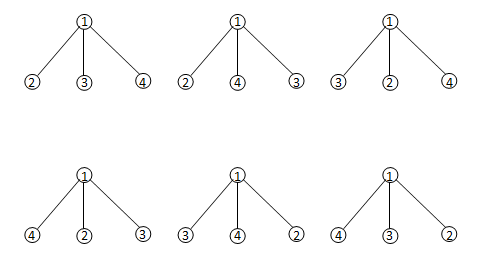
题意：给你一棵n个结点n-1条边的树，现在要给每个结点编号(1~n)，要求：①每个结点的儿子结点编号连续；②每棵子树的所有结点编号连续。连续的概念是，排序后是如i,i+1,i+2,…,j的形式。问你有多少种编号方式。

放上出题人的解题报告

从根节点开始，若一个节点有一个非叶子儿子节点，就会有两种选择，一个是当前最大的数，一个是当前存留最小的数；

即上述节点4，它仅有一个非叶子儿子节点，以该节点为根的子树合法方案数为2T*(S!)，此时T为节点3为根的子树的方案数，即2，所以T=2，节点4的叶子儿子节点数S=0，故2T*(S!)=2*2*(0!)=4

若有两个非叶子儿子节点的话，就只有一种排列方式了，以其中一个非叶子儿子节点为根的子树取当前最大的数，另一个非叶子儿子节点为根的子树取当前最小的数；

上述节点1即为有两个非叶子儿子节点的节点，以该节点为根的子树合法方案数为T*(S!)，此时T为以4为根的子树方案数与以3为根的子树方案数的乘积，即T=T4*T3=2T5*(0!)*2T2*(0!)=4T6*2T2=8，节点1的叶子儿子节点数S=0，故T*(S!)=8*(0!)=8

而如果有一个节点有多于两个非叶子儿子节点，那都是无解的；

另外叶子节点由于是按顺序排列的，所以会对结果造成n！的影响。

上述节点1即为有3个叶子儿子节点的节点，它的叶子儿子节点可以有n!种编号方式，故上述有3!=6种编号方案

dfs一遍，求一下总的方案数即可

需要提及的一点是，该题需要扩充系统栈，否则可能会遇到Runtime Error(STACK_OVERFLOW)

方式是只需在代码头部添加

#pragma comment(linker, "/STACK:1024000000,1024000000")

有不懂的地方欢迎提出来，我会尽快予以解答，谢谢！

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<stdlib.h>
#include<cmath>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 100005;
const int inf = 1000000000;
const int mod = 1000000007;
int c[N];
__int64 f[N];
bool w[N];
vector<int> s[N];
__int64 dfs(int k)
{
    __int64 sum=1;
    w[k]=true;
    int t=s[k].size();
    if(k==1)
        t++;
    if(t==1)
    {
        c[s[k][0]]++;
        return 1;
    }
    for(int i=0;i<s[k].size();i++)
        if(!w[s[k][i]])
            sum=(sum*dfs(s[k][i]))%mod;//printf("k=%d sum=%I64d c[k]=%d cha=%d\n",k,sum,c[k],s[k].size()-1-c[k]);
    if(t-1-c[k]<2)
        return 2*sum*f[c[k]]%mod;
    else if(t-1-c[k]>2)
        return 0;
    else
        return sum*f[c[k]]%mod;
}
int main()
{
    int t,i,n,u,v,k=1;
    for(i=f[0]=1;i<=100000;i++)
        f[i]=f[i-1]*i%mod;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        if(n==1)
        {
            printf("Case #%d: 1\n",k++);
            continue;
        }
        for(i=1;i<=n;i++)
            s[i].clear();
        memset(c,0,sizeof(c));
        memset(w,false,sizeof(w));
        for(i=1;i<n;i++)
        {
            scanf("%d%d",&u,&v);
            s[u].push_back(v);
            s[v].push_back(u);
        }
        printf("Case #%d: %I64d\n",k++,dfs(1));
    }
    return 0;
}

菜鸟成长记