OpenMP: OpenMP并行数目与并行体对运行效率的影响

       接下来再做一个测试，将并行和串行的循环次数设置为100，即将上例的main函数中：

for(int i = 0; i < 10000;i++)

更改为：

for(int i = 0; i < 100;i++)

然后分别运行10次，其结果如下表所示：

次数	串行	并行
1	0.00285003	0.007350087
2	0.00288031	0.00385478
3	0.0028603	0.00231841
4	0.00275407	0.0092762
5	0.00280949	0.00980167
6	0.00281462	0.00538499
7	0.00286081	0.00538858
8	0.00281103	0.00424682
9	0.00281309	0.00892829
10	0.00280026	0.00370494
平均值	0.002825401	0.006025477

      从上面的分析结果可见，在循环100次的时候，只有极少数情况下并行计算比串行计算所需的时间要少，许多情况下并行需要更多的时间，这与我们设计并行程序的初衷是截然相反的。出现这种情况的原因之一就是，在分发并行的时候，系统也是需要消耗资源的，如果用于并行分发所耗的时间大于并行计算中节约的时间，那么这种情况下的并行计算就显得毫无意义，正如上例中的测试。所以，在并行计算中，并不是所有的并行计算都比串行计算要节约时间，具体要看并行的任务是否值得去做并行计算。还有一个重要的原因就是每次并行的线程数目，由于计算机CPU同时支持的并行线程有限，不可能指定并行100次， CPU在同一时刻就能运行100个线程。另外，由于这个比较程序的计算量非常小，很容易受到系统中其他因素的影响而导致计算结果的不稳定，所以，建议在进行测试时，尽量将计算量稍微调大一点，同时每次测试时应尽量保证运行环境相近，以减少系统中其他程序对测试结果的干扰。

      下面用一个例子更能说明并行数目与程序运行效率间的关系，设置并形体中的计算量都一样，每次只是并行的次数不同，具体代码如下：

//File: Test02.cpp
#include<omp.h>
#include<iostream>
using namespace std;

//循环测试函数
void test02()
{
      for(inti=0;i<5000000;i++)
      {
            for(intj=0;j<1000;j++);
      }
}

int main()
{
      cout<<"这是一个新的并行测试程序!\n";
      cout<<"请输入并行次数：\n";
      intN=1;
      cin>>N;
      cout<<"开始进行计算...\n";
      double start = omp_get_wtime( );//获取起始时间
#pragmaomp parallel for
      for(inti = 0; i < N; i++)
      {
            test02();
      } 

      double end = omp_get_wtime( );//获取结束时间

      cout<<"计算耗时为："<<end -start<<"\n";

      cin>>end;

      return0;
}

      在近似的测试环境中分别对并行1次（相对于串行）、2次、3次等参数进行测试，其结果如下表：

N	计算耗时(s)	N	计算耗时(s)
1	13.3731	12	27.526
2	13.343	13	28.9753
3	13.2072	14	28.0228
4	13.7742	15	29.4308
5	13.5256	16	28.5016
6	14.0692	17	41.1712
7	14.4321	18	41.3934
8	15.2443	24	47.6976
9	27.5141	25	55.7176
10	28.201	32	60.9475
11	29.0979	33	69.7519

      计算时间与并行次数之间的关系如下图所示：

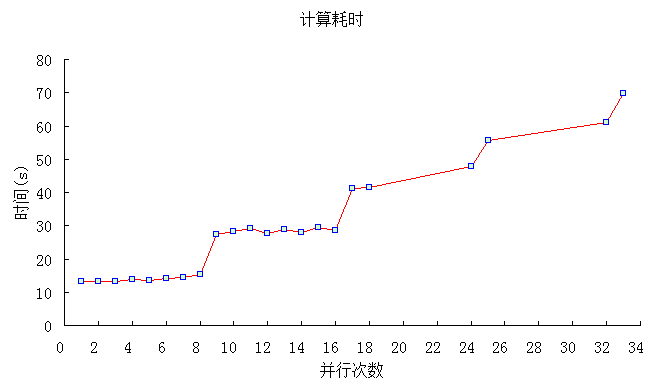
      从以上分析结果可知，在并形体中计算量相同的情况下，在计算机ＣＰＵ物理线程数目以内的并行次数可以得到更好的效果。这也可以很好的解释并行中线程数目设置的限制问题，如当设置９个并行线程时，由于计算机最多只支持８个线程，那第９个线程理所当然就不能和前面８个线程处于同一起跑线，它只能排在这８个线程的后面。假定第１到第８个线程是处于第一排，这一排的８个线程将会同时起步运行，而第９个到第１６个处于第二排，它们则要在第一排后面起步，依次类推。每一时刻，都只会有８个线程在进行计算，而并行的结束是以所有的线程运行结束为标志，因此，最后那个线程（或者说最慢的那个线程）将决定并行结束的时间，所以线程越多，那么排队就越长，并行结束的时间相应就会增长。当然，具体一队中有多少个循环，可以通过schedule来设定，关于schedule后面将会详细介绍。

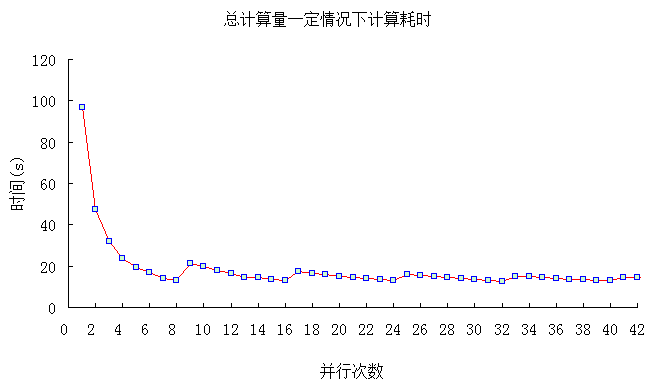
      当然，上面的分析是基于并形体中计算量相同的前提，但有些情况下并形体的计算量与并行次数有着密切关系，譬如说总计算量一定的情况下，任何设置合理的并行次数对整个程序的运行起着至关重要的作用。如下例子，并行计算的总计算量一定，即如果设置并行次数越多，则并形体中的计算量越小。代码如下：

//File: Test03.cpp
#include<omp.h>

#include<iostream>

using namespace std;

//循环测试函数

void test03(int space)
{
      for(inti=0;i<space;i++)
      {
            for(intj=0;j<1000;j++);
      }
}


int main()
{
      inttotal=36288000;
      cout<<"在总计算量一定的情况下测试程序!\n";
      cout<<"请输入并行次数：\n";
      intN=1;
      cin>>N;

      intspace =total/N;

      cout<<"开始进行计算...\n";

      double start = omp_get_wtime( );//获取起始时间

#pragmaomp parallel for

      for(inti = 0; i < N; i++)
      {
            test03(space);
      } 

      double end = omp_get_wtime( );//获取结束时间
      cout<<"计算耗时为："<<end -start<<"\n";
      cin>>end;

      return0;
}

      分别设置并行次数从１到４２进行测试，测试结果如下表所示：

N	计算耗时	N	计算耗时	N	计算耗时	N	计算耗时
1	96.9828	14	14.3488	27	14.9022	40	12.8593
2	47.2697	15	13.7259	28	14.3302	41	14.7085
3	31.8575	16	12.8605	29	14.0329	42	14.3195
4	23.5635	17	17.213	30	13.6062	50	14.2404
5	19.2746	18	16.551	31	13.1146	60	13.5563
6	16.7957	19	15.819	32	12.8218	80	12.8094
7	14.2741	20	14.9696	33	15.0214	100	13.2439
8	12.8982	21	14.3318	34	14.7972	200	12.8838
9	21.3869	22	13.8786	35	14.4498	400	12.8444
10	19.7044	23	13.3461	36	14.0154	1000	12.8158
11	17.9848	24	12.9017	37	13.7218	2000	12.7411
12	16.4976	25	15.9088	38	13.3481
13	14.5436	26	15.5088	39	13.0619

      比较结果如下图所示：

      由上图中可以很明显的看出，当并行数目达到计算机ＣＰＵ最多线程数目时（测试计算机上ＣＰＵ支持８线程），其计算效率将达到比较好的效果。假定计算机支持的最多线程为ｎ，并行数目在０～ｎ之间，计算效率逐渐增加，达到ｎ时效率极高，当增加到ｎ＋１个并行数目时，计算效率会骤降，但在ｎ＋１与２ｎ之间，计算效率同样也会逐渐增加，当达到２ｎ＋１时，又会骤降，随着并行数目不断增加，该规律将会不断的重现。

      所以，综合以上两个测试例子也不难发现，并非并行数目越多，其计算效率就越高，具体效率跟程序结构以及计算机有着密切的联系。

相关程序源码下载地址：
http://download.csdn.net/detail/xwebsite/3843187