图像处理特征不变算子系列之DoG算子（五）

图像处理特征不变算子系列之DoG算子（五）

[email protected]

http://blog.csdn.net/kezunhai

           在前面分别介绍了：图像处理特征不变算子系列之Moravec算子（一）、图像处理特征不变算子系列之Harris算子（二）、图像处理特征不变算子系列之SUSAN算子（三）和图像处理特征不变算子系列之FAST算子（四）。今天我们将介绍另外一个特征检测算子---DoG算子， DoG算子是由Lowe D.G.提出的，对噪声、尺度、仿射变化和旋转等具有很强的鲁棒性，能够提供更丰富的局部特征信息，本文将对DoG算子进行详细地分析。

           在开始介绍DoG之前，有必要对尺度空间有一定的了解。尺度空间最早是由Tony Lindeberg提出的，并不断的发展和完善。日常生活中，我们自觉或不自觉的在使用尺度的概念。举个我们个人自觉的经历，当我们读小学的时候，同学间互相询问来自哪个组；当我们读中学的时候，同学们互相询问自哪个村；当我们读高中的时候，同学们互相询问来自哪个镇；当读大学的时候，同学们互相询问来自哪个省？这里的组、村、镇、省就是我们不自觉使用的尺寸。还有一个例子，当我们打开google地图的时候，随着鼠标的滚动，地图会由五大洲逐渐定位到国家--》省---》市---》区---》街道办等，这也是尺度的表现。

           1）尺度空间

           在尺度空间中，尺度越大图像就越模糊，尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟目标由远及近人对目标的感知过程。那为什么要讨论尺度空间呢？因为在用机器视觉系统分析未知场景时，机器并不知道图像中物体的尺度，只有通过对图像的多尺度描述，才能获得对物体感知的最佳尺度。如果在不同尺度上，对输入的图像都能检测到相同的关键点特征，那么在不同尺度下也可以实现关键点的匹配，从而实现关键点的尺度不变特性。尺度空间描述的就是图像在不同尺度下的描述，如果对尺度空间有兴趣，请参考Tony Lindeberg的论文：Scale-Space。

         2）金字塔多分辨率

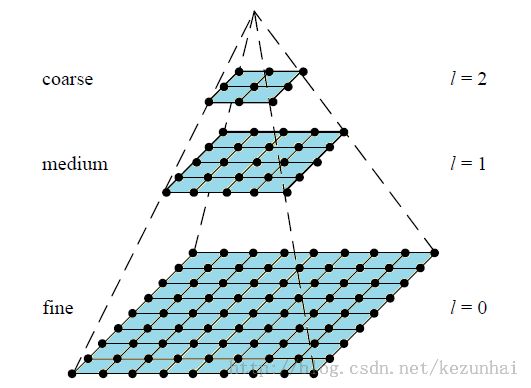
           常常有人会将DoG与图像金字塔弄混，从而导致对SIFT算法第一步构造DoG不甚理解。这里首先介绍下金字塔多分辨率。金字塔是早起图像多尺度的表示形式，图像金字塔一般包括2个步骤，分别是使用低通滤波平滑图像；对图像进行降采样（也即图像缩小为原来的1/4，长宽高缩小为1/2），从而得到一系列尺寸缩小的图像。金字塔的构造如下所示：

图像金字塔也正如其名，是以一个降采样的形式来表示图像的多分辨率，类似一个金字塔形状。

          3）高斯平滑滤波

          高斯核是唯一可以产生多尺度空间的核，细节分析可以参考：Scale-space theory: A basic tool for analysing structures at different scales。一个图像的尺度空间L(x,y,σ) ,定义为原始图像I(x,y)与一个可变尺度的2维高斯函数G(x,y,σ)卷积运算。 二维空间高斯函数：

尺度空间表示为：

高斯模版是圆对称的，且卷积的结果使原始像素值有最大的权重，距离中心越远的相邻像素值权重也越小。高斯模糊另一个重要的性质就是线性可分，使用二维矩阵变换的高斯模糊可以通过在水平和竖直方向各进行一维高斯矩阵变换相加得到。

            4）多尺度与多分辨率

           尺度空间表达和金字塔多分辨率表达之间最大的不同是：
          （1）尺度空间表达是由不同高斯核平滑卷积得到，在所有尺度上有相同的分辨率；
          （2）金字塔多分辨率表达每层分辨率减少固定比率。
所以，金字塔多分辨率生成较快，且占用存储空间少；而多尺度表达随着尺度参数的增加冗余信息也变多。多尺度表达的优点在于图像的局部特征可以用简单的形式在不同尺度上描述；而金字塔表达没有理论基础，难以分析图像局部特征。

          5）拉普拉斯金字塔

          结合尺度空间表达和金字塔多分辨率表达，就是在使用尺度空间时使用金字塔表示，在计算机视觉中最有名莫过于拉普拉斯金字塔。对于拉普拉斯不清楚的可以参考：http://homepages.inf.ed.ac.uk/rbf/HIPR2/log.htm。这里简单介绍下介绍下拉普拉斯金字塔。

          拉普拉斯金字塔顾名思义就是通过对图像进行拉普拉斯操作，然后进行一个降采样的过程。具体来说就是：原始图像作为金字塔的底层，也即0层，称为g0，对0层图像g0进行进行拉普拉斯金操作，得到第一层图像g1；接着对第一层图像进行拉普拉斯操作，得到第二层图像g2，依次类推，并进行一个降采样，如此构造拉普拉斯金字塔。这里只是做简单的介绍，如果还要了解更多细节信息，请参考论文：The Laplacian pyramid as a compact image code。高斯金字塔对应于opencv里的cvPyrDown函数，实现图像的向下采样功能；拉普拉斯金字塔对应于opencv里的cvPyrUp函数，实现图像的重建或恢复功能。

         6）DoG金字塔

          DoG（Difference of Gaussian）其实是对高斯拉普拉斯LoG的近似，在某一尺度上的特征检测可以通过对两个相邻高斯尺度空间的图像相减，得到DoG的响应值图像D(x,y,σ)。具体来说：

         （1）分别对原图进行相邻尺度的高斯滤波

          对原图的高斯滤波表示如下：

将上面滤波得到的两幅图像g1和g2相减得到：

如果将该公式进行简化写（SIFT中的写法），则变成如下：

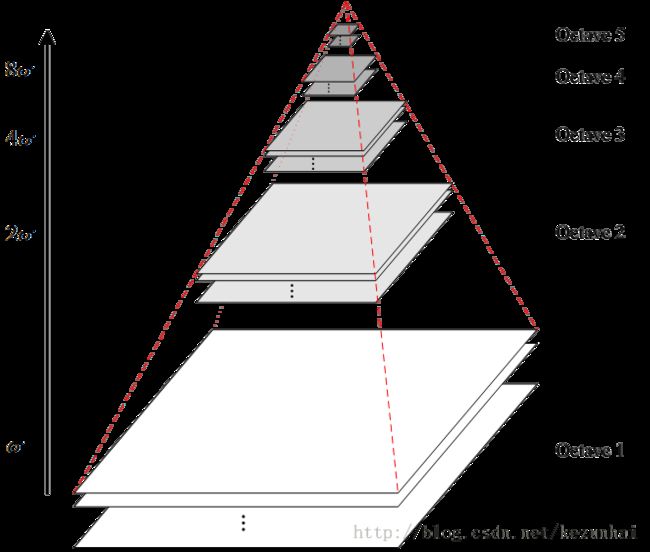
        为了得到DoG图像，首先要构造高斯金字塔，高斯金字塔在多分辨率金字塔的基础上加入了高斯滤波，也就是对金字塔每层图像采用不同的参数sigma进行了高斯卷积，使得金字塔的每层有多张图片组成为一个Octave，每组有多张（也叫层interval）图像。在SIFT算子中，很多人对Octave和Interval不太了解，现在应该清楚了吧（每个Octave是由同一大小的图像，经过不同sigma高斯滤波得到的，而Interval则表示的是同一个sigma高斯滤波的图像）。另外，降采样时，金字塔上边一组图像的第一张图像（最底层的一张）是由前一组（金字塔下面一组）图像的倒数第三张隔点采样得到，图像表示如下：

下面代码贴出opencv中构造高斯金字塔的代码：

void SIFT::buildGaussianPyramid( const Mat& base, vector<Mat>& pyr, int nOctaves ) const
{
    vector<double> sig(nOctaveLayers + 3);
    pyr.resize(nOctaves*(nOctaveLayers + 3));

    // precompute Gaussian sigmas using the following formula:
    //  \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2
    sig[0] = sigma;
    double k = pow( 2., 1. / nOctaveLayers );
    for( int i = 1; i < nOctaveLayers + 3; i++ )
    {
        double sig_prev = pow(k, (double)(i-1))*sigma;
        double sig_total = sig_prev*k;
        sig[i] = std::sqrt(sig_total*sig_total - sig_prev*sig_prev);
    }

    for( int o = 0; o < nOctaves; o++ )
    {
        for( int i = 0; i < nOctaveLayers + 3; i++ )
        {
            Mat& dst = pyr[o*(nOctaveLayers + 3) + i];
            if( o == 0  &&  i == 0 )
                dst = base;
            // base of new octave is halved image from end of previous octave
            else if( i == 0 )
            {
                const Mat& src = pyr[(o-1)*(nOctaveLayers + 3) + nOctaveLayers];
                resize(src, dst, Size(src.cols/2, src.rows/2),
                       0, 0, INTER_NEAREST);
            }
            else
            {
                const Mat& src = pyr[o*(nOctaveLayers + 3) + i-1];
                GaussianBlur(src, dst, Size(), sig[i], sig[i]);
            }
        }
    }
}

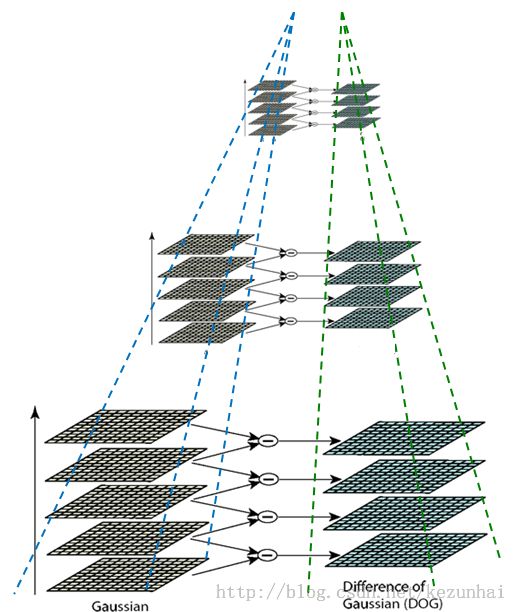
高斯金字塔构造完成后，就可以求DoG，如图所示：

opencv中实现的DoG的代码为：

void SIFT::buildDoGPyramid( const vector<Mat>& gpyr, vector<Mat>& dogpyr ) const
{
    int nOctaves = (int)gpyr.size()/(nOctaveLayers + 3);
    dogpyr.resize( nOctaves*(nOctaveLayers + 2) );

    for( int o = 0; o < nOctaves; o++ )
    {
        for( int i = 0; i < nOctaveLayers + 2; i++ )
        {
            const Mat& src1 = gpyr[o*(nOctaveLayers + 3) + i];
            const Mat& src2 = gpyr[o*(nOctaveLayers + 3) + i + 1];
            Mat& dst = dogpyr[o*(nOctaveLayers + 2) + i];
            subtract(src2, src1, dst, noArray(), DataType<sift_wt>::type);
        }
    }
}

            7）根据DoG求角点

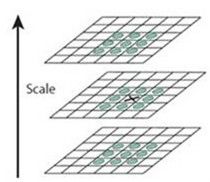
            理论：三维图中的最大值和最小值点是角点，如图所示：

           X标记当前像素点，绿色的圈标记邻接像素点，用这个方式，最多检测相邻尺度的26个像素点。如果它是所有邻接像素点的最大值或最小值点，则X被标记为特征点，如此依次进行，则可以完成图像的特征点提取。

 更多信息请参考：

        1、DoG (Difference of Gaussian)角点检测：http://blog.csdn.net/abcjennifer/article/details/7639488

        2、SIFT原理与源码分析：DoG尺度空间构造：http://blog.csdn.net/xiaowei_cqu/article/details/8067881

作者：kezunhai 出处：http://blog.csdn.net/kezunhai 欢迎转载或分享，但请务必声明文章出处。