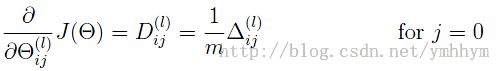Stanford ML - Neural Networks: Learning 神经网络训练学习
对于神经网络分类的问题,如果最终是K个分类,那么每个分类都用一个K维的向量表示结果;只有一个元素为1,其余为0,其中1对应所在的分类。这样神经网络的正则化Cost Function为:
可以看出,这跟逻辑回归的代价方程完全一致。只是因为有K个输出单元,需要把它们全部加起来。这里的正则项可以理解为所有层Theta值的平方和。这里的问题仍然是求Theta使得Cost Function取值最小。不管是梯度下降,还是其他高级公式,核心问题都需要求偏导。
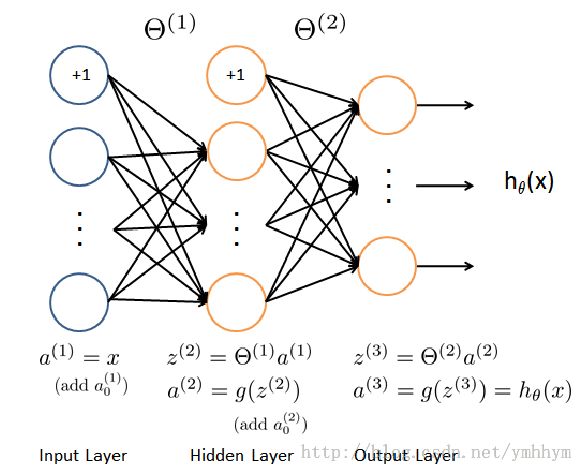
神经网络里面的偏导计算起来有些复杂,朴素的来说就是对所有的训练集数据,向前传播计算a,再后向传播计算delta,根据这两个值最终算出需要的偏导。贴图如下:
前向传播比较简单,从输入开始,按照作业的例子如下:
后向传播呢,其实就是倒着算每一层的误差。因为输出层的a已经通过前向传播计算出来了,这层的误差可以表示为a-y;然后倒推前面几层的误差:
这里g(z),也就是sigmoid function,的导数为:
最终正则化之后的偏导:
这个过程用程序表示如下,纯粹的套用公式,用向量计算:
X = [ones(m, 1), X];
z2 = X * Theta1';
a2 = sigmoid(z2);
a2 = [ones(size(a2, 1), 1), a2];
a3 = sigmoid(a2 * Theta2');
y_matrix = zeros(m, num_labels);
for i = 1:m
y_matrix(i, y(i)) = 1;
end
J_matrix = -(y_matrix .* log(a3) + (1 - y_matrix) .* log(1 - a3)) / m;
J = sum(sum(J_matrix, 2));
Theta1_reg = Theta1(:, 2:end);
Theta2_reg = Theta2(:, 2:end);
reg = sum(sum(Theta1_reg .^ 2, 2));
reg = reg + sum(sum(Theta2_reg .^ 2, 2));
reg = reg * lambda / (2*m);
J = J + reg;
% Compute gradients
delta3 = a3 - y_matrix;
delta2 = delta3 * Theta2;
delta2 = delta2(:, 2:end) .* sigmoidGradient(z2);
Theta1_grad = Theta1_grad + delta2' * X;
Theta1_grad = Theta1_grad / m;
Theta1_grad(:, 2:end) = Theta1_grad(:, 2:end) + Theta1(:, 2:end) * lambda / m;
Theta2_grad = Theta2_grad + delta3' * a2;
Theta2_grad = Theta2_grad / m;
Theta2_grad(:, 2:end) = Theta2_grad(:, 2:end) + Theta2(:, 2:end) * lambda / m;
在计算过程中需要对初始的theta值做随机化处理,如果全部相等会丢失信息。一般可以取-EPSILON到+EPSILON。再有呢,可以用偏导极限的思想对求出的Theta做一下验证,这两种方式计算出来的Theta值应该非常接近。这种梯度检查代价很高,验证之后最终应用神经网络的时候需要去掉。
最后有如何选择神经网络结构的问题:
1. 输入层单元是确定的,等于输入特征的维度
2. 输出层单元也是确定的,等于分类的数目
3. 隐藏层可以是一层或者多层,每层可以有同样数目的单元,比如输入的3倍、5倍,通常越多越好。但多了计算代价应该也会大。