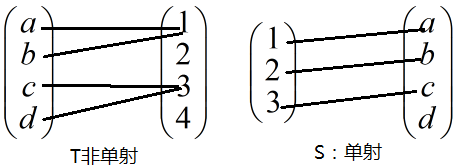线性代数(十三) : 可逆映射与逆映射

0 可能需要复习的知识

映射与矩阵

1 恒等映射

对于一个映射(叫函数也行)T：X->X 如果T(a)=a (a是域X中的元素)则称T为域X上的恒等映射(或者恒等函数)

通常可以记作Ix.

2 可逆映射

(i)已知一个映射T：X->Y ，若存在一个映射S：Y->X 满足 S o T= Ix(x上的恒等映射)并且

T o S=Iy(Y上的恒等映射)则称T为可逆(invertible)映射(可逆函数),称S为T的逆映射(逆函数)

3 逆映射的是唯一的

证明：

已知映射T ：X->Y ，映射S和H都是T的逆映射,则有：

S o T=Ix  T o S = Iy 

H o T=Ix  T o H = Iy 

S = Ix o S = H o T o S = H o (T o S )= H o Iy = H

所以我们得出结论 一个映射的逆映射如果存在(注意我们还没有讨论存在性)那么它是唯一的.

4 满射与单射

(i)对于映射T :X->Y,如果Y中的每一个元素y都存在X中的元素x使得T(x)=y则称T为满射

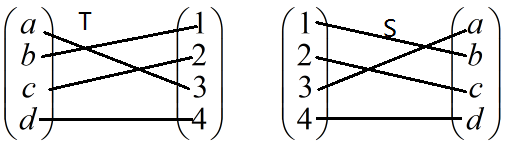
满射与非满射的例子：

(ii)对于映射T :X->Y,如果Y中的每一个元素y都最多存在X中的一个元素x使得T(x)=y则称T为单射

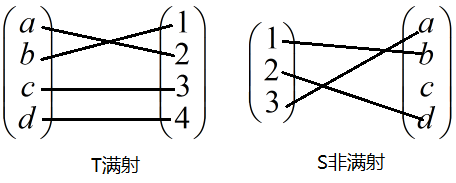
满射与非满射的例子：

5 单射和满射以及可逆性的关系

一个映射T:X->Y是可逆的当且仅当该映射既是单射又是满射

证明：

(i)这里用反证法证明必要性,即如果是可逆映射，则一定是单射并且是漫射：

假设T不是满射,则存在a,b∈X(a≠b) 并且T(a)=T(b)=y(y∈Y)此时明显T不是单射，假设T的逆映射是S:Y->X

则 S(T(a))=a因为T(a)=T(b)=y(y∈Y),因此S(T(b))=a,这就表明S o T不是恒等映射.因此矛盾。

所以可逆映射一定是单射。

(ii)假设T不是满射，即存在y∈Y且不存在x∈X满足T(x)=y.这样假设T的逆映射为S：Y->X。

此时 T(S(y))≠y 因此这与S是T的逆映射矛盾。因此可逆映射一定是满射。

(iii)下边证明充分性：即已知一个映射T：X->Y既是单射又是满射，证明T是可逆的

由于T是满射并且是单射对任意y∈Y存在x∈X满足T(x)=y.对于每一对这样的x和y这样我们可以构造一个映射S:Y->X 使得S(y)=x。

这样S(T(x))=x,T(S(y))=y。因此S o T=Ix   T o S=Iy. 这样就证明了构造的映射S是T的逆映射.

如下图这样T是一个一对一的映射并且是满射，很容易构造出逆映射：

这样我们就证明了一个判断可逆性的一个充分必要条件，或者说等价条件。

一个矩阵可以认为是一个线性映射，一个可逆的线性映射对应一个可逆矩阵。关于这些会在下节介绍