后缀数组

后缀数组是字符串处理的一个重要工具。它由原字符串的所有后缀的字典排序而得，具有较高的检索效率。

字符串aabaaaab的所有后缀

[编辑]基本概念

一、字符串的大小比较： 关于字符串的大小比较，是指通常所说的 “ 字典顺序 ” 比较， 也就是对于两个字符串 u 、v ，令 i 从 1 开始顺次比较 u[i] 和 v[i] ，如果u[i]=v[i] 则令 i 加 1 ，否则若 u[i]<v[i] 则认为 u<v ，u[i]>v[i] 则认为 u>v，比较结束。如果 i>len(u) 或者 i>len(v) 仍比较不出结果，那么若 len(u)<len(v)则认为 u<v ， 若 len(u)=len(v) 则 认 为 u=v ，若 len(u)>len(v) 则 u>v 。

 注：从字符串的大小比较的定义看，字符串s的所有后缀中任其中一对(u,v)不可能会相等，因为必要条件 len(u) ≠ len(v)不可能满足。所以任一字符串s中有len(s)个互不相同的后缀。我们可以将s的所有后缀排列，利用 后缀数组sa 与 名次数组rank 储存。 

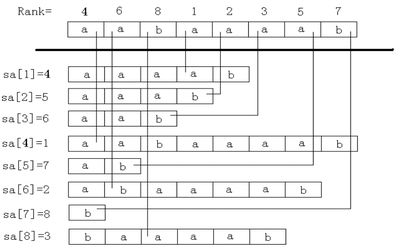
二、后缀数组sa：将s的n个后缀从小到大排序后将 排序后的后缀的开头位置 顺次放入sa中，则sa[i]储存的是排第i大的后缀的开头位置。简单的记忆就是“排第几的是谁”。

三、名次数组rank：rank[i]保存的是suffix(i)｛后缀｝在所有后缀中从小到大排列的名次。则 若 sa[i]=j，则 rank[j]=i。简单的记忆就是“你排第几”。

对于 后缀数组sa 与 名次数组rank ，有

rank[ sa[i] ]=i （这是很重要的一点，通过sa与rank的关系可以求出后缀数组）

字符串aabaaaab的sa数组与rank数组

由此可看出，后缀数组sa 与名次数组rank的关系为互逆关系。

[编辑]倍增算法

一、主要思路：倍增，s[i..i + 2^k − 1]的排名通过s[i..i + 2^{k − 1} − 1]和s[i + 2^{k − 1}..i + 2^k − 1]的排名得到。

二、简要过程：已知每个长度为2^{k − 1}的字符串的排名，则可作为每个长度为2^k的字符串求排名的关键字xy，s[i..i + 2^k − 1]第一关键字x为s[i..i + 2^{k − 1} − 1]的排名，第二关键字y为s[i + 2^{k − 1}..i + 2^k − 1]的排名。以字符串aabaaaab为例：

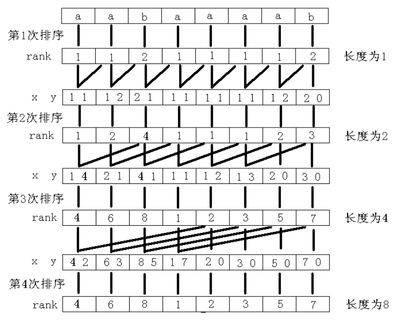
1. k=0,对每个字符开始的长度为2⁰ = 1的子串进行排序，得到rank[1..8]={1,1,2,1,1,1,1,2}
2. k=1,对每个字符开始的长度为2¹ = 2的子串进行排序：由k=0的rank得关键字xy[1..8]={11,12,21,11,11,11,12,20}，得到rank[1..8]={1,2,4,1,1,1,2,3}
3. k=2,对每个字符开始的长度为2² = 4的子串进行排序：由k=1的rank得关键字xy[1..8]={14,21,41,11,12,13,20,30}，得到rank[1..8]={4,6,8,1,2,3,5,7}
4. k=3,对每个字符开始的长度为2³ = 8的子串进行排序：由k=2的rank得关键字xy[1..8]={42,63,85,17,20,30,50,70}，得到rank[1..8]={4,6,8,1,2,3,5,7}

注意：在排序过程中，rank[]可以有相同排名，但是sa[]排第几是没有相同的（就像Excel的排序，sa相当于编号，rank相当于排名）。这点可以从程序中体现。建议读者跟踪一下程序体会一下。

整个过程如图：

倍增算法的计算过程

三、时间复杂度分析：每一趟的计数排序的时间复杂度是O(n)，排序的次数共log n次，总的时间复杂度为O(n log n)。

算法代码如下：
void sorting(int j)//基数排序
{
	memset(sum,0,sizeof(sum));
	for (int i=1; i<=s.size(); i++) sum[ rank[i+j] ]++;
	for (int i=1; i<=maxlen; i++) sum[i]+=sum[i-1];
	for (int i=s.size(); i>0; i--) tsa[ sum[ rank[i+j] ]-- ]=i;//对第二关键字计数排序，tsa代替sa为排名为i的后缀是tsa[i] 

	memset(sum,0,sizeof(sum));
	for (int i=1; i<=s.size(); i++) sum[ rank[i] ]++;
	for (int i=1; i<=maxlen; i++) sum[i]+=sum[i-1];
	for (int i=s.size(); i>0; i--) sa[ sum[ rank[ tsa[i] ] ]-- ]= tsa[i]; //对第一关键字计数排序
	//构造互逆关系 
}

void get_sa()
{
	int p;
	for (int i=0; i<s.size(); i++) trank[i+1]=s[i];
	for (int i=1; i<=s.size(); i++) sum[ trank[i] ]++;
	for (int i=1; i<=maxlen; i++) sum[i]+=sum[i-1];
	for (int i=s.size(); i>0; i--) 
		sa[ sum[ trank[i] ]-- ]=i;
	rank[ sa[1] ]=1;
	for (int i=2,p=1; i<=s.size(); i++)
	{
		if (trank[ sa[i] ]!=trank[ sa[i-1] ]) p++;
		rank[ sa[i] ]=p;
	}//第一次的sa与rank构造完成
	for (int j=1; j<=s.size(); j*=2)
	{
		sorting(j);
		trank[ sa[1] ]=1; p=1; //用trank代替rank 
		for (int i=2; i<=s.size(); i++)
		{
			if ((rank[ sa[i] ]!=rank[ sa[i-1] ]) || (rank[ sa[i]+j ]!=rank[ sa[i-1]+j ])) p++;
			trank[ sa[i] ]=p;//空间要开大一点，至少2倍
		}
		for (int i=1; i<=s.size(); i++) rank[i]=trank[i];
	}
}

[编辑]线性时间复杂度算法

基本上有两个不同的线性算法，分别是Juha Karkkainen和Peter Sanders在2003年提出的[KS03]以及Pang Ko和Srinivas Aluru在2003年提出的[KA03]。Ge Nong、Sen Zhang和Wai Hong Chan后来在[NZC08]中对[KA03]提出了一种改进。

[编辑]KS03

算法简述：先给字符串S末尾补3个$。再对字符串中在3i+1, 3i+2起始的连续三个字母构造一个新的字符集，并对该字符集进行基数排序（radix sort）。接着构造T = S[1:3]S[4:6]……$S[2:4]S[5:7]……$，对T递归算出后缀数组，就可以得到S[3i+1:]（suffix(3i+1)）和S[3i+2:]在后缀数组中的顺序了。

然后只要再将S[3i:]插入到正确的位置。由于S[3i:]可以看作S[3i]S[3i+1:]、所以S[3i:]跟S[3j+1:]的大小比较相当于(S[3i], S[3i+1:])跟(S[3j+1], S[3j+2]:)的比较。因此通过一次基数排序可以将S[3i:]与S[3i+1:]排序（S[3i+2:]与S[3i+1:]的相对顺序保持不变）。同理S[3i:]与S[3j+2:]的比较相当于(S[3i], S[3i+1:])与(S[3j+2], S[3(j+1):])的比较，再进行一次基数排序即可将S的所有后缀的顺序排好。

[编辑]KA03

[编辑]基本观察

如果s[i:] < s[i+1:]那么给i标记“小”，不然标记“大”；s[len:]也就是$，给它双重标记。计算标记只要将字符串倒着扫描一遍。（认为$是最小的字符）

对所有的后缀按照其首字母装入桶中。假设桶为n，容易发现，标记为“大”的后缀（大后缀）都是小于nnn…的，而标记为“小”的后缀（小后缀）都是大于nnn…的。因此在桶中，大后缀应该在小后缀的左边。另外，大后缀的下一个后缀在其左边，小后缀的下一个后缀在其右边。

[编辑]算法

大后缀的数目和小后缀的数目总有一个不超过|S| / 2的。不妨假设小后缀比较少。如果我们对所有小后缀递归地排序了，就可以通过下面的方法对所有后缀进行排序。

先将桶中的所有小后缀按照递归计算的结果排序。这一步是线性的。

顺序扫描所有桶。第一个桶是$，里面只有后缀$。对每个扫描到的后缀S[i:]，如果它前一个后缀（即S[i-1:]）是大后缀，就把它调整到它的桶的最前方，并固定它的位置（也就是桶的头后移一位，或者可以认为桶不再包括它了）。正确性是因为，我们读到的后缀都已经是顺序的了，而且根据读取过的东西立刻调整S[i-1:]的位置，每次调整一定会把被调整的东西放到正确的位置，这是因为一个桶内的后缀的从第二个字母开始排序的顺序跟整体的后缀顺序是一致的。由于大后缀一定会被之前的某个东西调整，所以能保证在读到接下来它的时候，它已经是被调整到正确的位置上了。

如果是大后缀多，算法只要修改为从后向前扫描桶，桶里也从后向前，然后对上一个后缀的调整是调整到桶的末尾。证明中略不同的是，最后一个桶假设是x，那么x就是最大的出现过的字符，可以证明桶x中的后缀都是大后缀。而大后缀已经排序好了，所以从后向前扫描时，是按照最终排序结果的倒序读取的。

[编辑]子问题字符集构造

对所有小后缀排序就只能把这些小后缀相间的部分缩成字符集，但是变长字符集是个大问题，如果字符集中一个字符是另一个的前缀，就无法比较由这个字符集组成的字符串的大小了。

解决办法是substring定义为包含后面一个小后缀的首字母，即如果两个相邻的小后缀，分别在i和j位置开始，那么substring定义为S[i..j]。这样，如果一个substring是另一个的前缀，例如长的那个是“小大大大大大小”而短的是“小大大小”，根据前面提的大比小靠左的规则，短的要靠后，长的靠前，顺序就可以确定了。

[编辑]排序子问题字符集

原始方法：

把所有字母装桶（具体的桶），再根据它是substring的第几个字母分别挪到第几行，不同的桶内的字符划条竖线以示区别。根据第二行的分割，对第一行的桶进行细分（怎么做不用再说了吧），再根据第三行的分割对第一行进行细分，……字符集就做好了。其实这个桶的性质很好，都跟棵树一样了。那么，就只用把同一个桶中的如果有多个substring，对那个桶排序就可以了吧，但是比较可惜这里做不了太多优化，只能把原字符串中连续出现单字符桶缩成一个，递归完了之后，可以在当前的桶的基础上挪一挪。（不做这个优化就不用挪桶里的东西）

改进的方法（来自yangzhe1990）：

这个方法的来源是[NZC08]。做法是：对S的所有字符按照首字母装桶，对桶内再按照大后缀在前小后缀在后的规则排好。然后顺序扫描这个桶。对于每个扫描到的后缀S[i:]，如果它上一个后缀S[i-1:]是大后缀，就将它调整到它所在桶中的第一个，并固定它在桶中的位置；如果S[i-1:]是小后缀，就将它调整到它所在桶中的小后缀的第一个，并固定它的位置。

正确性证明懒得写了…详见yangzhe1990。谁有空来整理一下。

[编辑]最长公共前缀

求出了rank和sa数组还不够，通常我们需要由rank与sa数组计算出一个辅助工具height数组——最长公共前缀(LCP)。

height 数组： 定义height[i]=suffix(sa[i-1]) 和 suffix(sa[i]) 的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。

由height数组可得，对于j和k ，不妨设rank[j]<rank[k], 则有以下性质：suffix(j) 和 suffix(k) 的最长公共前缀为 height[rank[j]+1],height[rank[j]+2], height[rank[j]+3], … ,height[rank[k]] 中的最小值。

以"aabaaaab"为例，求后缀"abaaaab"和后缀"aaab"的最长公共前缀，如图，可见其最长公共前缀等于1。

计算后缀"abaaaab"和后缀"aaab"的最长公共前缀

所以说，计算最长公共前缀是一个典型的RMQ问题。

如果直接按照sa的顺序一个一个求解，每一次比较最坏的时间复杂度是O(len(s))，一共要比较len(s)次，所以时间复杂度是O(len(s)²)。这样求height数组是非常慢的，而且没有用到之前所说height数组的性质。

那么，如何高效地计算后缀间的最长公共前缀呢？

当然是使用之前所说的性质。定义h[i]为suffix(i)和前一名次后缀的最长公共前缀{sa[ rank[ i ]-1 ]}。由性质可得，

。

 简单的证明如下：设suffix(k)是排在suffix(i-1)前一位的后缀，则它们的最长公共前缀显然是h[i-1]。那么，suffix(k+1)显然将排在suffix(i)的前面。并且，suffix(k+1)&suffix(i) 相对于 suffix(k)&suffix(i-1)来说就是同时去掉了第一位，即少了一位的匹配数。所以suffix(i)和前一名次后缀的最长公共前缀至少是h[i-1]-1。

显然，我们可以按照h数组的顺序计算height。时间复杂度分析：求一次height后位数-1，一共有len(s)个后缀，所以只能退len(s)次，也就是说，求解的时间复杂度是O(len(s))。

算法代码如下：
void get_height()
{
	for (int i=1,j=0; i<=s.size(); i++)//用j代替上面的h数组
	{
		if (rank[i]==1) continue;
		for (; s[i+j-1]==s[ sa[ rank[i]-1 ]+j-1 ]; ) j++;//注意越界之类的问题 
		height[ rank[i] ]=j;
		if (j>0) j--;
	}
}

[编辑]构造后缀树

利用最长公共前缀数组（lcp数组），使用一个栈就可以构造出相应的后缀树。

[编辑]后缀数组的应用

先提出后缀数组的几种常用技巧：

1. 建议多找找与height数组的关联。
2. 将几个字符串贴在一起，用特殊符号间隔开：如aab与aaab，可合并成aab$aaab。
3. 二分+分组（思想）的方法：枚举出答案后，就能将合法的情况划分到一个组判断。

以下列举出几个后缀数组的应用供大家思考，也可在讨论页讨论。

1. 求两个后缀的最长公共前缀
2. 求字符串的可重叠的最长重复子串：如ababa可重叠的最长重复子串是aba
3. 求字符串的不可重叠的最长重复子串：如ababa不可重叠的最长重复子串是ab [提示：想想建议3]
4. 计算不相同子串的个数：如aaaa的不相同子串数是4
5. 计算最长回文子串：如aabaaaab的最长回文子串是6(baaaab)。[提示：想想建议2]
6. 求两个字符串的最长公共子串：如aaba与abac的最长公共子串是aba。

[编辑]例题

1. [poj3261]
2. [poj2774]
3. [poj1743]
4. [poj3415]

[编辑]参考资料

• 国家集训队2009论文《后缀数组——处理字符串的有力工具》 罗穗骞
• 国家集训队2004论文《后缀数组》 许智磊
• 《程序设计中实用的数据结构》 王建德 吴永辉
• [KA03] Juha Karkkainen and Peter Sanders, Simple Linear Work Suffix Array Construction, Proceedings of the 30th International Colloquium on Automata, Languages and Programming, LNCS 2719, Springer, pp. 943-955, 2003.
• [KS03] Pang Ko and Srinivas Aluru, Space-efficient linear time construction of suffix arrays, Proceedings of the 14th Annual Symposium on Combinatorial Pattern Matching, pp. 200-210, 2003.
• [NZC08] Ge Nong, Sen Zhang and Wai Hong Chan, Two Efficient Algorithms for Linear Suffix Array Construction, 2008.
• http://yangzhe1990.wordpress.com/2012/09/14/suffix-array-suffix-tree/

原文地址：点击打开链接