Delta-wave

Problem Description

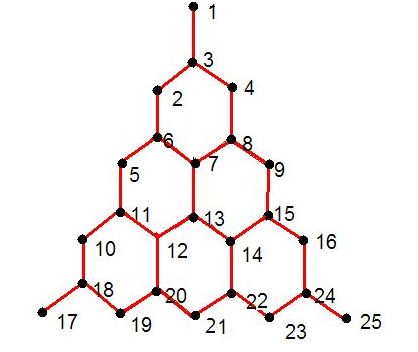
A triangle field is numbered with successive integers in the way shown on the picture below.



The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.

Write the program to determine the length of the shortest route connecting cells with numbers N and M.

 

 

Input

Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).

 

 

Output

Output should contain the length of the shortest route.

 

 

Sample Input

   
   
   
   

    
    
    
    6 12 
   
   
   
   

 

 

Sample Output

   
   
   
   

    
    
    
    3
   
   
   
   

 

 

Source

Ural Collegiate Programming Contest 1998

 

 

Recommend

lcy

分析：此题有多种规律找！我的规律是：若m（其中m是较小的那个数）是该层的奇数项，那判断n是否在以m为顶点的三角范围内 ，若在则步数=2*相差层数-1+(或-，根据n是该层的奇偶项判断)1；若m为偶数项，则在前面公式上再加1，而此时三角范围则是m-1和m+1的并；当n不在范围内时，只要在上面判断后的式子基础上再加上n与三角范围边界的差即可。如下图，m=4 n=10，步数=2*2-1+1+|10-12|=6。

代码：

#include <iostream>
#include <cmath>
using namespace std;

void swap(int& m, int& n)
{
 int tmp = m;
 m = n;
 n = tmp;
}

void getlayer(int v, int& layer, int& nums) // layer是层数, nums是该层第几个数
{
 float sq = sqrtf((float)v);
 layer = (int) ceil(sq);
 nums = v - (layer-1)*(layer-1);
}

int main()
{
 int m, n;
 int mLayer = 0, mNums = 0, nLayer = 0, nNums = 0;
 int out, flag, left, right;

 while (cin>>m>>n)
 {
  if (m > n)
   swap(m, n);

  getlayer(m, mLayer, mNums);
  getlayer(n, nLayer, nNums);

  if (nLayer == mLayer)
   out = nNums - mNums;
  else
  { 
   int layer = nLayer-mLayer;
   if (mNums%2 == 0)
   {
    flag = 1;
    left = m-1+(2*mLayer+layer-2)*layer;
    right = m+1+(2*mLayer+layer)*layer;
   }
   else
   {
    flag = 0;
    left = m+(2*mLayer+layer-2)*layer;
    right = m+(2*mLayer+layer)*layer;
   }

   if (n >= left && n <= right)
   {
    if (nNums%2==0)
     out = 2*layer-1+flag;
    else
     out = 2*layer-1+1+flag;
   }
   else if (n < left)
    out = 2*layer-1+1+flag+left-n;
   else if (n > right)
    out = 2*layer-1+1+flag+n-right;
  }
  cout<<out<<endl;
 }

 return 0;
}

另一种用广度优先收索算法的解答，不过会超时！仅供参考！

代码：

#include <iostream>
#include <cmath>
using namespace std;

#define  MAX 5000000
struct node
{
 int v;
 int last;
}state[MAX];

int m, n;
int nLayer; // 目标数字所在层

void swap(int& m, int& n)
{
 int tmp = m;
 m = n;
 n = tmp;
}

void getlayer(int v, int& layer, int& nums) // layer是层数, nums是该层第几个数
{
 float sq = sqrtf((float)v);
 layer = (int) ceil(sq);
 nums = v - (layer-1)*(layer-1);
}

void getlayerbound(int layer, int& min, int& max)
{
 min = 1+(layer-1)*(layer-1);
 max = layer*layer;
}

void init()
{
 if (m > n)
  swap(m, n);
 state[0].v = m;
 state[0].last = 0;
}

bool repeat(node state[], int tail, int val)
{
 for (int i = 0; i <= tail; ++i )
 {
  if (state[i].v == val)
   return true;
 }
 return false;
}

bool find(int val)
{
 if (val == n)
  return true;
 return false;
}

bool isinbound(int v, int min, int max)
{
 if (v >= min && v <= max)
  return true;
 return false;
}

bool expend(node state[], int head, int& tail, node tmpnode)
{
 int layer, nums;
 int min, max;

 getlayer(tmpnode.v, layer, nums);
 getlayerbound(layer, min, max);

 if (layer == nLayer || nums%2 == 0)  // 当目标数字同层时或为偶数时同层收索
 {
  if (isinbound(tmpnode.v+1, min, max) && !repeat(state, tail, tmpnode.v+1))
  {
   state[++tail].v = tmpnode.v+1;
   state[tail].last = head;
   if (find(state[tail].v))
    return true;
  }
  if (isinbound(tmpnode.v-1, min, max) && !repeat(state, tail, tmpnode.v-1))
  {
   state[++tail].v = tmpnode.v-1;
   state[tail].last = head;
   if (find(state[tail].v))
    return true;
  }
 }

 if (nums%2 != 0)
 {
  if (!repeat(state, tail, tmpnode.v+2*layer))
  {
   state[++tail].v = tmpnode.v+2*layer;
   state[tail].last = head;
   if (find(state[tail].v))
    return true;
  }
 }
 return false;
}

void printpath(node state[], int pos, int& nums)
{
 if (state[pos].v != m)
  printpath(state, state[pos].last, ++nums);
 else
 {
  cout<<nums<<endl;
 }
}

void bfs()
{
 int head, tail;
 int out = 0, tmp;
 node tmpnode;

 getlayer(n, nLayer, tmp);
 head = tail = 0;
 while (head<=tail && tail < MAX)
 {
  tmpnode = state[head];
  if (expend(state, head, tail, tmpnode))
  {
   printpath(state, tail, out);
   break;
  }
  ++head;
 }
}

int main()
{
 while (cin>>m>>n)
 {
  init();
  bfs();
 }

 return 0;
}