poj 2552 JOJ 2083 The Bottom of a Graph 图的强连通性
| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 3066 | Accepted: 1227 |
Description
Let n be a positive integer, and let p=(e1,...,en) be a sequence of length n of edges ei∈E such that ei=(vi,vi+1) for a sequence of vertices (v1,...,vn+1). Then p is called a path from vertex v1 to vertex vn+1 in G and we say that vn+1 is reachable from v1, writing (v1→vn+1).
Here are some new definitions. A node v in a graph G=(V,E) is called a sink, if for every node w in G that is reachable from v, v is also reachable from w. The bottom of a graph is the subset of all nodes that are sinks, i.e., bottom(G)={v∈V|∀w∈V:(v→w)⇒(w→v)}. You have to calculate the bottom of certain graphs.
Input
Output
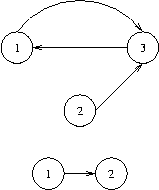
Sample Input
3 3 1 3 2 3 3 1 2 1 1 2 0
Sample Output
1 3 2
Source
void Tarjan(int u) //Tarjan
{
int v;
node[u].DFN=node[u].LOW=(++idx);
instack[u]=true;
stack[++top]=u;
for(Edge*p=node[u].first; p; p=p->next)
{
v=p->adj;
if(!node[v].DFN)
{
Tarjan(v);
if(node[v].LOW<node[u].LOW)
node[u].LOW=node[v].LOW;
}
else if(instack[v]&&node[v].DFN<node[u].LOW)
node[u].LOW=node[v].DFN;
}
if(node[u].DFN==node[u].LOW)
{
b_cnt++;
do
{
v=stack[top--];
instack[v]=false;
node[v].belongs=b_cnt;
}
while(u!=v);
}
}
void Tarjan_SCC() //StronglyConnectedComponent
{
int i,t1,t2;
b_cnt=idx=top=0;//b_cnt 新图的点数
for(i=1; i<=N; i++)
if(!node[i].DFN)
Tarjan(i);
if(b_cnt<=1)
{
for(int i=1;i<=N;i++)
{
if(i!=1) printf(" ");
printf("%d",i);
}
printf("/n");
}
else
{
Init2();
memset(hash,-1,sizeof(hash));
for(i=1; i<=N; i++)
{
flag[i]=true;
for(Edge*p=node[i].first; p; p=p->next)
if(node[i].belongs!=node[p->adj].belongs
&&hash[node[i].belongs]!=node[p->adj].belongs)
{
hash[node[i].belongs]=node[p->adj].belongs;
InsertEdge2(node[i].belongs,node[p->adj].belongs);
}
else
if(node[i].belongs==node[p->adj].belongs&&!flag[p->adj])
{
now[node[i].belongs].sum++;
flag[p->adj]=true;
}
}
/*if(node[i].belongs!=node[p->adj].belongs)
out[node[i].belongs]++,in[node[p->adj].belongs]++;*/
int k=0,kk=0;
for(i=1; i<=b_cnt; i++)
{
k=0;
for(Edge*p=now[i].first; p; p=p->next)//计算出度数
k++;
if(k==0) {f[i]=true;kk++;}
}
/*t1=t2=0;
for(i=1; i<=b_cnt; i++)
{
if(!in[i]) t1++;
if(!out[i])t2++;
}*/
if(kk==0)
{
printf("/n");
}
else
{
int m=0;
for(int i=1;i<=N;i++)
if(f[node[i].belongs])
{
if(m!=0) printf(" ");
printf("%d",i);
m++;
}
printf("/n");
}
}
}