深度学习系列(四):什么是稀疏编码
上节使用简单方法阐述了自编码问题与简单操作,本节将正式开始探索深度学习的相关问题,第一个问题就是稀疏编码。
关于稀疏编码需要理解的几点:
(1)什么是稀疏编码?
(2)为什么要稀疏编码?
(3)稀疏编码的实现途径。
首先什么是稀疏编码?在这之前先看看稀疏表示。
从一个简单的例子说起,相信大多数人学过线性代数或者矩阵论之类的课程吧,再线性代数中,最初始的时候就会学到关于如何判断一大堆向量线性的相关或者不相关性,进而确定一组线性无关组。这里比如说空间中一个向量X是一个三维坐标点吧,用(x,y,z)表示。假设现在有一堆点X1(1,0,0);X2(0,1,0);X3(0,0,1);X4(4,3,5);X5(2,1,4)……等等吧,那么我们是不是可以找到这一大堆向量的最大线性无关组其实就可以用X1,X2,X3来表示,其他的任何向量Xi都可以用这三个向量来线性表示,当然用X1,X2,X3来表示任何一个向量来表示是最简单情况,你一个向量同样可以用X1,X2,X3,X4,X5来表示,不过这个多两个待确定系数而已。好了现在假设我们已知有X1~X10这十个向量,那么同空间中有一个向量我们就可以用X1~X10这十个向量线性表示,就有10个待确定系数。但是我们事先是知道一个向量只需要用X1,X2,X3来表示即可了,那么我们可以让上面需要确定的10个参数中的后7个参数约束为0即可,那么其实这个过程就是一种稀疏表示思想。
可以看出稀疏表示就是找到空间中的一组基,用这组基可以扩展到空间中的任何向量。
同样的我们可以用一系列的基信号来表示(至于用什么基,这里谈一下,上面我们看出这个图其实无非是一个函数,只不过不太好直接写出函数表达式表示而已,如果能,傅里叶变换告诉我们,什么函数都可以分解成一系列正弦余弦函数表示吧),所以我们可以找到一系列基信号如下:
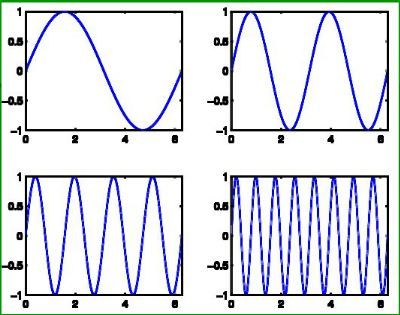
当然可能不止4个,可以有更多,越多表示的越准确,这也反过来说明稀疏表示的一个问题,那就是稀疏到什么程度?上述信号,如果只用前2个基信号表示的话,肯定会差很多,用前3个表示,好点,越多基信号,表示的越准确,然而另一个问题可以看出,用两个表示,极其稀疏,表示起来也简单,但是效果差,用n个,很不稀疏,但是效果好,所以一个信号到底要稀疏表示到什么程度需要自己去设计的,也就是说这是一个变化的参数。
把上述抽象成数学表示,假设原始信号为X,基信号为d1~dp,这些基信号组合成X的权值参数分别为a1~ap,那么也就是说
X=a1*d1+a2*d2+…+ap*dp=[d1,d2,…,dp]*[a1,a2,…,ap]’;如下所示

那么 α 就是我们要稀疏表示的吧,如果它之中0元素越多,就认为越稀疏表示了。这里再展开一点,就是实际中我们怎么去确定 α 中那些为0那些又不为0呢?其实在实际中我们并不是非得说某个 αi 非得为0,而是通过限制所有的 α 之和为一个比较小的数,或者把这些和加入目标函数的惩罚项中,我们保证所有的 α 之和必须优化到我们设置的很小的一个数C就认为是稀疏表示了。
再来看一个例子,我们可以把一个颜色空间稀疏表示成下面这个样子吧:

好了,从上述可以看出稀疏表示的好处在于降低表示复杂度,更直白的原因其实就是减少系数参数,通过稀疏表示,可以充分发挥数据所含有的信息,去掉冗余的数据信息,达到最大化利用数据,这一点是非常重要的。
有了上面的认识,我们再来看看深度神经网络中的稀疏编码表示是如何进行的。还是以简单的三层自编码网络为例:

在这个网络中,我们可能可以学习到样本数据的特征集s,和一个将特征集从特征空间转换到样本数据空间的基向量 A,那么我们可以建立目标函数
,表示的意思就是让输出与输入的误差和越小越好,优化这个J找到最佳网络系数即可。那么这是没有稀疏表示的目标函数,这是特征集s可能含有许多重复的,冗余的特征在里面,而这些冗余的特征在理论上我们是需要干掉的。那么在此基础上我们设计带稀疏性质的目标函数如下:
这样上式前第一部分是利用基向量将特征集重构为样本数据所产生的误差,第二部分为稀疏性惩罚项(sparsity penalty term),用于保证特征集的稀疏性。
当然这是最原始的稀疏表示构造方式,要达到此网络稀疏的目的,光这样子是不行的,在真实的网络中还需要加一些其他的限制才可以,然而其稀疏思想确是这样的,详细的内容可以参考:
稀疏编码自编码表达
在集成的深度学习工具箱中,关于稀疏编码的设计上,通常我们只需要设计一个限制系数C用于限制稀疏程度就可以了,或者有时候这个C是一定的,比如0.05,所有的网络都给这个参数即可,但是了解稀疏编码对于我们理解深度学习的参数设计优化等等都是很有必要的。
