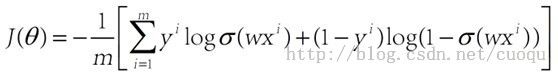机器学习理论与实战:逻辑回归
转载自:http://blog.csdn.net/marvin521/article/details/9263483
从这节算是开始进入“正规”的机器学习了吧,之所以“正规”因为它开始要建立价值函数(cost function),接着优化价值函数求出权重,然后测试验证。这整套的流程是机器学习必经环节。今天要学习的话题是逻辑回归,逻辑回归也是一种有监督学习方法(supervised machine learning)。逻辑回归一般用来做预测,也可以用来做分类,预测是某个类别^.^!线性回归想比大家都不陌生了,y=kx+b,给定一堆数据点,拟合出k和b的值就行了,下次给定X时,就可以计算出y,这就是回归。而逻辑回归跟这个有点区别,它是一种非线性函数,拟合功能颇为强大,而且它是连续函数,可以对其求导,这点很重要,如果一个函数不可求导,那它在机器学习用起来很麻烦,早期的海维赛德(Heaviside)阶梯函数就因此被sigmoid函数取代,因为可导意味着我们可以很快找到其极值点,这就是优化方法的重要思想之一:利用求导,得到梯度,然后用梯度下降法更新参数。
下面来看看逻辑回归的sigmoid函数,如(图一)所示:
(图一)
(图一)中上图是sigmoid函数在定义域[-5,5] 上的形状,而下图是在定义域[-60,60]上的形状,由这两个图可以看出,它比较适合做二类的回归,因为严重两级分化。Sigmoid函数的如(公式一)所示:
(公式一)
现在有了二类回归函数模型,就可以把特征映射到这个模型上了,而且sigmoid函数的自变量只有一个Z,假设我们的特征为X=[x0,x1,x2…xn]。令,当给定大批的训练样本特征X时,我们只要找到合适的W=[w0,w1,w2…wn]来正确的把每个样本特征X映射到sigmoid函数的两级上,也就是说正确的完成了类别回归就行了,那么以后来个测试样本,只要和权重相乘后,带入sigmoid函数计算出的值就是预测值啦,很简单是吧。那怎么求权重W呢?
要计算W,就要进入优化求解阶段咯,用的方法是梯度下降法或者随机梯度下降法。说到梯度下降,梯度下降一般对什么求梯度呢?梯度是一个函数上升最快的方向,沿着梯度方向我们可以很快找到极值点。我们找什么极值?仔细想想,当然是找训练模型的误差极值,当模型预测值和训练样本给出的正确值之间的误差和最小时,模型参数就是我们要求的。当然误差最小有可能导致过拟合,这个以后再说。我们先建立模型训练误差价值函数(cost function),如(公式二)所示:
(公式二)
(公式二)中Y表示训练样本真实值,当J(theta)最小时的所得的theta就是我们要求的模型权重,可以看出J(theta)是个凸函数,得到的最小值也是全局最小。对其求导后得出梯度,如(公式三)所示:
(公式三)
由于我们是找极小值,而梯度方向是极大值方向,因此我们取负号,沿着负梯度方向更新参数,如(公式四)所示:
(公式四)
按照(公式四)的参数更新方法,当权重不再变化时,我们就宣称找到了极值点,此时的权重也是我们要求的,整个参数更新示意图如(图二)所示:
(图二)
原理到此为止逻辑回归基本就说完了,下面进入代码实战阶段:
- from numpy import *
- def loadDataSet():
- dataMat = []; labelMat = []
- fr = open('testSet.txt')
- for line in fr.readlines():
- lineArr = line.strip().split()
- dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
- labelMat.append(int(lineArr[2]))
- return dataMat,labelMat
- def sigmoid(inX):
- return 1.0/(1+exp(-inX))
上面两个函数分别是加载训练集和定义sigmoid函数,都比较简单。下面发出梯度下降的代码:
- def gradAscent(dataMatIn, classLabels):
- dataMatrix = mat(dataMatIn) #convert to NumPy matrix
- labelMat = mat(classLabels).transpose() #convert to NumPy matrix
- m,n = shape(dataMatrix)
- alpha = 0.001
- maxCycles = 500
- weights = ones((n,1))
- for k in range(maxCycles): #heavy on matrix operations
- h = sigmoid(dataMatrix*weights) #matrix mult
- error = (labelMat - h) #vector subtraction
- weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
- return weights
梯度下降输入训练集和对应标签,接着就是迭代跟新参数,计算梯度,然后更新参数,注意倒数第二句就是按照(公式三)和(公式四)来更新参数。
为了直观的看到我们得到的权重是否正确的,我们把权重和样本打印出来,下面是相关打印代码:
- def plotBestFit(weights):
- import matplotlib.pyplot as plt
- dataMat,labelMat=loadDataSet()
- dataArr = array(dataMat)
- n = shape(dataArr)[0]
- xcord1 = []; ycord1 = []
- xcord2 = []; ycord2 = []
- for i in range(n):
- if int(labelMat[i])== 1:
- xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
- else:
- xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
- fig = plt.figure()
- ax = fig.add_subplot(111)
- ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
- ax.scatter(xcord2, ycord2, s=30, c='green')
- x = arange(-3.0, 3.0, 0.1)
- y = (-weights[0]-weights[1]*x)/weights[2]
- ax.plot(x, y)
- plt.xlabel('X1'); plt.ylabel('X2');
- plt.show()
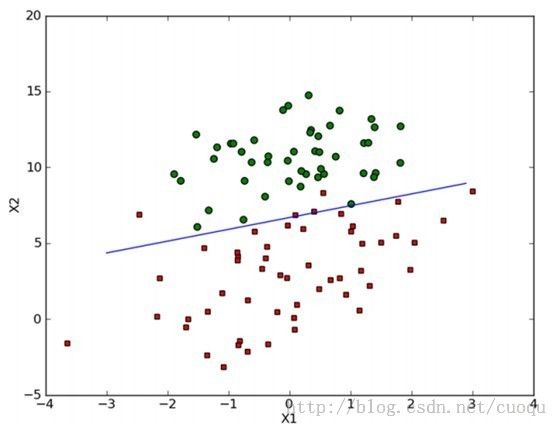
打印的效果图如(图三)所示:
(图三)
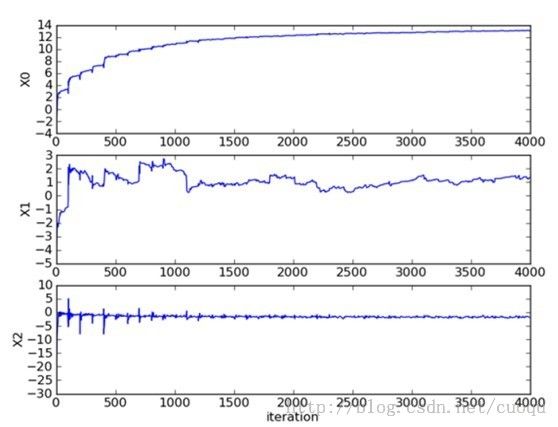
可以看出效果蛮不错的,小错误是难免的,如果训练集没有错误反而危险,说到这基本就说完了,但是考虑到这个方法对少量样本(几百的)还行,在实际中当遇到10亿数量级时,而且特征维数上千时,这种方法很恐怖,光计算梯度就要消耗大量时间,因此要使用随机梯度下降方法。随机梯度下降算法和梯度下降算法原理一样,只是计算梯度不再使用所有样本,而是使用一个或者一小批来计算梯度,这样可以减少计算代价,虽然权重更新的路径很曲折,但最终也会收敛的,如(图四)所示
(图四)
下面也发出随机梯度下降的代码:
- def stocGradAscent1(dataMatrix, classLabels, numIter=150):
- m,n = shape(dataMatrix)
- weights = ones(n) #initialize to all ones
- for j in range(numIter):
- dataIndex = range(m)
- for i in range(m):
- alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
- randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
- h = sigmoid(sum(dataMatrix[randIndex]*weights))
- error = classLabels[randIndex] - h
- weights = weights + alpha * error * dataMatrix[randIndex]
- del(dataIndex[randIndex])
- return weights
最后也给出一个分类的代码,只要把阈值设为0.5,大于0.5划为一类,小于0.5划为另一类就行了,代码如下:
- def classifyVector(inX, weights):
- prob = sigmoid(sum(inX*weights))
- if prob > 0.5: return 1.0
- else: return 0.0
总结:
优点:计算量不高,容易实现,对现实数据也很容易描述
缺点:很容易欠拟合,精度可能也会不高
参考文献:
[1] machine learning in action. Peter Harrington
[2] machine learning.Andrew Ng