单源最短路问题

最短路问题是图论中最基础的问题，在面试题中出现的次数也很多，很多类似最少步数等问题都能转化到最短路问题，这篇文章介绍单源最短路问题的两种算法。单源最短路问题是固定一个起点，求它到其他所有点的最短路问题，如果只求两个固定点之间的最短路，看起来要简单很多，但其实复杂度是一样的，所以我们广泛的讨论单源最短路问题。

1Bellman-Ford算法

我们定义从点s到目的地点i的距离为d[i]，这样我们需要i=0到i=E-1（E为顶点）时的所有的d[i]。

把问题划分成子问题，假设顶点j和i之间有一条边连着，那么d[i]=min{d[j]+(j到i的边的权值)}。

需要注意的是：如果图中有圈，比如i到j为3，j到i为4，我们不知道是先计算d[i]还是d[j]，这时这时只要把所有的d[i]初始化为INF（i不为s），我们先计算哪个就没有关系了。因为即使只要满足d[j]+(j到i的边的权值)比原来的d[i]小，我们就更新d[i]的值。

这样我们就可以直接利用这条递归关系写出代码如下：

struct edge{ int from, to , cost} //边的结构体：顶点from到顶点to的权值cost
edge es[MAX_E];   //边的数组
int d[MAX_V];   //距离的数组	
int V,E;     //顶点数和边数
void shortest_path(int s){
  for (int i=0;i<V;i++)
        d[i]=INF;
     d[s]=0;
  while(true)
   bool update=false;
  for(int i=0;i<E;i++)
     edge e=es[i];
   if(d[e.from]!=INF&&d[e.to]>d[e.form]+e.cost){ //从已经想连的顶点中找到满足条件的
       d[e.to]=d[e.from]+e.cost;
       update=true;  
      }
    }
  if(!update) break;  //所有顶点都更新过后，结束
}
}

复杂度：while最多循环|V|-1次，所以是O（|V|*|E|）。

注意：如果图中存在负圈（例：i到j为-1，j到i为-2），那么最短路径就沿着负圈一直无限循环。。。我们可以判定如果while的第|V|次循环也更新的话，那么就存在负圈。

2Dijkstra算法

Dijkstra算法是一种特殊情况，即当图中没有负边的情况，这种情况是很符合实际情况的，比如两个旅行目的地的距离。既然都是正数，那么我们可以想一下，如果d[j]还不睡最短距离，那么即使d[i]=d[j]+(权值)更新了，d[i]也不是最短距离。而且上段代码中每次对顶点V的循环中，要检查一遍和顶点相连的所有的边，这有点浪费时间。所以算法贪心的修改如下：

（1）找到最短距离确定的点，从它出发更新相邻顶点的距离。

（2）已经确定的点就不用再管了。

这个确定的点就是未使用过的顶点中，距离最小的顶点，因为没有负边，这个确定的点不会再之后的更新中变小。

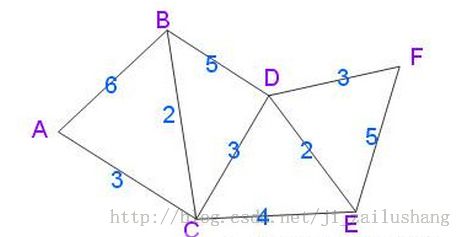
本图中：确定点的先后顺序依次为A，C，B，D，E，F

代码如下：

int cost[MAX_V][MAX_E] 
int d[MAX_V];   
bool used[MAX_V];
int V;
void dijkstra(int s){
  fill(d,d+V,INF);
  fill(used,used+V,false);
  d[s]=0;
  while(true){
  int v=-1;
  for(int u=0;u<V;u++){  //从未使用的顶点中选择一个距离最小的顶点（while的第一次循环选择的是点s）
   if(!used[u]&&(v==-1||d[u]<d[v])) 
     v=u;
   }
 if (v==-1) break;
  used[v]=true;
  for(int u=0;u<V;u++){
   d[u]=min(d[u],d[v]+cost[v][u]); //更新和确定的点相连的点的距离
   }
  }
}

这种写法的复杂度是O（|V|^2）,代码中大部分时间花在查找下一个使用的顶点上，我们可以使用好的数据结构保护好这个顶点，在有数值插入的情况下要得到集合中的最小值，那么最好的数据结构是堆，堆中元素有O（|V|）个，需要更新O（|E|)次，所以复杂度为O（|E|log|V|）。

下面用STL中的优先级队列（priority_queue实现）：

struct edge{int to, cost}
typedef pair<int ,int> P;   //first是最短距离，second是顶点编号
int d[MAX_V];   
vector<edge> G[MAX_V];//邻接表
int V;
void dijkstra(int s){
priority_queue<P,vector<p>,greater<p>> que;  //greater表示从小到大
  fill(d,d+V,INF);
  d[s]=0;
  que.push(P(0,s));
  while(!que.empty()){
  P p=que.top();  //取出确定点
   que.pop();
   int v=p.second;
   if(d[v]<p.first) continue;
  for(int i=0;i<G[v].size();i++)
  {
 edge e=G[v][i];  //边为从点v到点i
  if(d[e.to]>d[v]+e.cost;){
    d[e.to]=d[v]+e.cost;
   que.push(P(d[e.to],e.to)); //把更新的距离和点放进堆
   }
  }
}
}

如果使用斐波那契堆，性能还能提高，就是有点复杂。

总之在没有负边的情况下Dijkstra算法性能优于Bellman-Ford算法。所以这种方法非常重要，需要仔细专研其中原理。