特征变换以及维度下降——Linear Discriminant Analysis（三）

【原文：http://blog.csdn.net/jojozhangju/article/details/19626351】

6.Linear Discriminant Analysis应用实例以及相关实现

下面我们用LDA来进行一个分类的问题：假设一个产品有两个参数来衡量它是否合格，我们假设两个参数分别为：

所以我们可以根据上图表格把样本分为两类，一类是合格的，一类是不合格的，所以我们可以创建两个数据集类：

cls1_data = 
    2.9500        6.6300 
    2.5300        7.7900 
    3.5700        5.6500 
    3.1600        5.4700 

cls2_data = 
    2.5800        4.4600 
    2.1600        6.2200 
    3.2700        3.5200

其中cls1_data为合格样本，cls2_data为不合格的样本，我们算出合格的样本的期望值，不合格类样本的合格的值，以及总样本期望： 
E_cls1 = 
       3.0525        6.3850 
E_cls2 = 
       2.6700        4.7333 
E_all = 
       2.8886        5.6771 

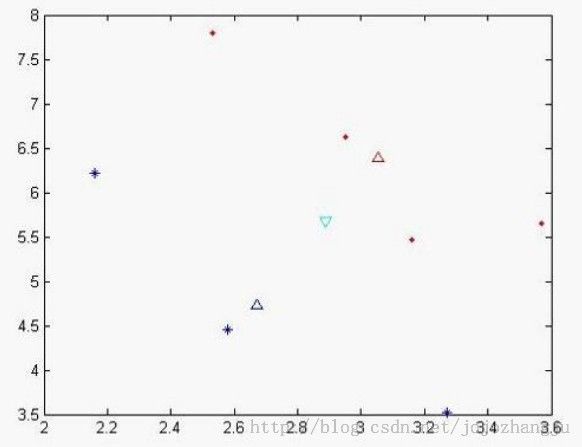
我们可以做出现在各个样本点的位置：

其中蓝色‘*’的点代表不合格的样本，而红色实点代表合格的样本，天蓝色的倒三角是代表总期望，蓝色三角形代表不合格样本的期望，红色三角形代表合格样本的期望。从x，y轴的坐标方向上可以看出，合格和不合格样本区分度不佳。 
我们可以计算出类间离散度矩阵和类内离散度矩阵： 

Sb = 
    0.0358        0.1547 
    0.1547        0.6681
Sw = 
    0.5909       -1.3338 
   -1.3338        3.5596 

算出特征值以及对应的特征向量：

L = 
    0.0000             0 
         0        2.8837 
对角线上为特征值，第一个特征值太小被计算机约为0了 与他对应的特征向量为 
V = 
   -0.9742     -0.9230 
    0.2256     -0.3848 
根据取最大特征值对应的特征向量：（-0.9230,-0.3848)，该向量即为我们要求的子空间，我们可以把原来样本投影到该向量后 所得到新的空间（2维投影到1维，应该为一个数字） 

new_cls1_data =   
   -5.2741 
   -5.3328 
   -5.4693 
   -5.0216 
为合格样本投影后的样本值 
new_cls2_data = 
   -4.0976 
   -4.3872 
   -4.3727 
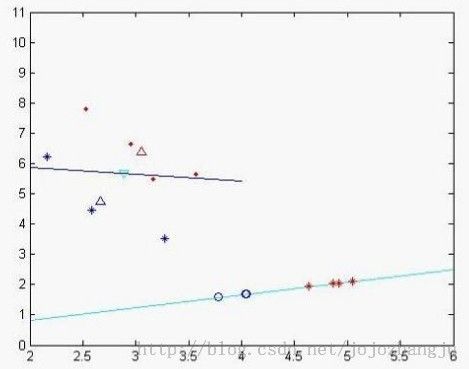
为不合格样本投影后的样本值，我们发现投影后，分类效果比较明显，类和类之间聚合度很高，我们再次作图以便更直观看分类效果

蓝色的线为特征值较小所对应的特征向量，天蓝色的为特征值较大的特征向量，其中蓝色的圈点为不合格样本在该特征向量投影下来的位置，二红色的‘*’符号的合格样本投影后的数据集，从中个可以看出分类效果比较好（当然由于x，y轴单位的问题投影不那么直观）。 

我们再利用所得到的特征向量，来对其他样本进行判断看看它所属的类型，我们取样本点 
（2.81，5.46）， 
我们把它投影到特征向量后得到：result = -4.6947 所以它应该属于不合格样本。 

实现代码：

LDA.m

 <span style="font-family:Microsoft YaHei;font-size:18px;">function [reduced_data,V]=LDA(data,N,reduced_dim)
 C=length(N);
 dim=size(data',1);
 % 计算每类样本在data中的起始、终止行数
 pos=zeros(C,2);
 for i=1:C
 START=1;
 if i>1
 START=START+sum(N(1:i-1));
 end
 END=sum(N(1:i));
 pos(i,:)=[START END];
 end
 % 每类样本均值
 UI=[];
 for i=1:C
 if pos(i,1)==pos(i,2)
 % pos(i,1)==pos(i,2)时，mean函数不能工作
 UI=[UI;data(pos(i,1),:)];
 else
 UI=[UI;mean(data(pos(i,1):pos(i,2),:))];
 end
 end
 % 总体均值
 U=mean(data);
 % 类间散度矩阵
 SB=zeros(dim,dim);
 for i=1:C
 SB=SB+N(i)*(UI(i,:)-U)'*(UI(i,:)-U);
 end
 % 类内散度矩阵
 SW=zeros(dim,dim);
 for i=1:C
 for j=pos(i,1):pos(i,2)
 SW=SW+(data(j,:)-UI(i,:))'*(data(j,:)-UI(i,:));
 end
 end
 % 该部分可以要，也可以不要
 SW=SW/sum(N);
 SB=SB/sum(N);
 % 计算特征值与特征向量
 matrix=pinv(SW)*SB;
 [V,D]=eig(matrix);
 condition=dim-reduced_dim+1:dim;
 V=V(:,condition);
 % 根据新的特征向量，将数据映射到新空间
 reduced_data=data*V;
 V
 end
 </span>

testlda.m

 <span style="font-family:Microsoft YaHei;font-size:18px;">data=[2.95 6.63; 2.53 7.79; 3.57 5.65;3.16 5.47;2.58 4.46; 2.16 6.22; 3.27 3.52];
 N=[4 3];
 [reduced_data,V]=LDA(data,N,1);
 data
 reduced_data
 new = [2.81 5.46]
 result = new * V;
 result</span>