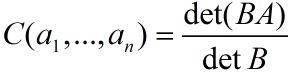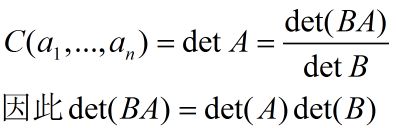线性代数(二十三) ： 行列式的乘法性质与其几何意义

本节定义行列式的一个新的性质，行列式的乘法性质

0 行列式函数D的三条性质：

(i)若存在ai=aj(i不等于j)则D=0

(ii)D是多重线性函数

(iii)D(e1,...,en) = 1

1 行列式的乘法性质

设A,B都是nxn的矩阵，则：
det(BA) = det(A)det(B)

2 行列式乘法性质的证明

根据矩阵乘法的性质可知BA的第j列为(BA)ej(其中ej为单位矩阵E的第j列)

同理A的第j列aj = Aej, 根据矩阵乘法的结合律有：

(BA)ej=BAej=Baj

于是根据上一节的内容可知 将 BA的行列式表示成函数形式有：

假设detB 不等于 0 定义函数C:

下边证明函数C满足函数D的三条性质(见之前的章节)则可以证明函数C是函数D本身

(i) 如果存在ai = aj (i不等于j) 则Bai = Baj 因此D(Ba1,...,Ban) = 0 ，因此C(a1,...,an) = 0 因此函数C 满足性质1,

(ii)Bai 是ai的线性函数, 又因为D是多重线性函数，因此C也是ai的多重线性函数(线性映射的复合仍是线性映射)，因此函数C满足性质2

(iii)若令ai = ei 则有：

因此函数C满足性质3，综上所述函数C满足行列式函数的三条性质，因此函数C就是行列式本身 因此：

3 行列式乘法性质的几何意义

一个矩阵可以看成是一个线性映射那么线性映射将一个单形映射为另一个单形 体积变为原来的|detB| 倍 ,由于任意单形都是若干开集的并。因此任意开集在映射B下的象的体积

(detBA)都是原体积(detA)的|detB|倍