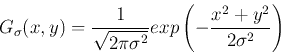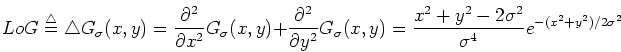log算子 和dog 算子
LOG算子
目录(?)[+]
背景引言
在博文差分近似图像导数算子之Laplace算子中,我们提到Laplace算子对通过图像进行操作实现边缘检测的时,对离散点和噪声比较敏感。于是,首先对图像进行高斯暖卷积滤波进行降噪处理,再采用Laplace算子进行边缘检测,就可以提高算子对噪声和离散点的Robust, 这一个过程中Laplacian of Gaussian(LOG)算子就诞生了。本节主要介绍LOG算子基本理论数学分析比较多些,最后,贴出用Mathcad软件实现的LOG代码。
基本理论
高斯卷积函数定义为:
而原始图像与高斯卷积定义为:
因为:
所以Laplacian of Gaussian(LOG)![]() 可以通过先对高斯函数进行偏导操作,然后进行卷积求解。公式表示为:
可以通过先对高斯函数进行偏导操作,然后进行卷积求解。公式表示为:
和
因此,我们可以LOG核函数定义为:
高斯函数和一级、二阶导数如下图所示:
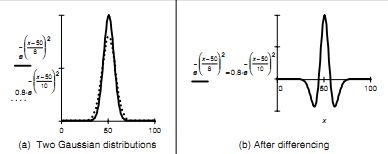
Laplacian of Gaussian计算可以利用高斯差分来近似,其中差分是由两个高斯滤波与不同变量的卷积结果求得的
从两个平平滑算子的差分得出的是二阶边缘检测,反直观。近似计算可能如下图所示。图中一维空间,不同变量的两个高斯分布相减形成一个一维算子
参考代码
计算LOG算子模板系数的式(4.27)实现如下代码:
此函数包括一个正规函数,它确保模板系数的总和为1. 以便在均匀亮度区域不会检测到边缘。
参考资料
[1] Laplacian of Gaussian http://fourier.eng.hmc.edu/e161/lectures/gradient/node9.html.
[2] Rafael C.Gonzalez, Rechard E.Woods at. el , "Digital Image Processing Using MatLab (Second Editon)",Gatesamark Publishing.
关于Image Engineering & Computer Vision的更多讨论与交流,敬请关注本博和新浪微博songzi_tea
DOG算子
目录(?)[+]
背景简述
Difference of Gaussian(DOG)是高斯函数的差分。它是可以通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果,即去噪过程,这里的Gaussian和高斯低通滤波器的高斯一样,是一个函数,即为正态分布函数。同时,它对高斯拉普拉斯LoG(博文LOG算子介绍了实现原理)的近似,在某一尺度上的特征检测可以通过对两个相邻高斯尺度空间的图像相减,得到DoG的响应值图像。
基本理论
首先,高斯函数表示定义为:
其次,两幅图像的高斯滤波表示为:
最后,将上面滤波得到的两幅图像g1和g2相减得到:
即:可以DOG表示为:
在具体图像处理中,就是将两幅图像在不同参数下的高斯滤波结果相减,得到DoG图。具体步骤如下所示:
第一步,计算不同参数下的DOG;
在图1,图2,图3,三种图像给了不同参数下的高斯滤波输出的效果,如下图所示:
图1:一个高斯平滑参数为0.3,另一个高斯平滑参数为0.4
图2:一个高斯平滑参数为0.6,另一个高斯平滑参数为0.7
图3 :一个高斯平滑参数为0.7,另一个高斯平滑参数为0.8
第二步,根据DOG,求角点。
根据理论:三维图中的最大值和最小值点是角点,如图所示(此图片来源于自网络):
标记红色当前像素点,绿色的圈标记邻接像素点,用这个方式,最多检测相邻尺度的26个像素点。如果它是所有邻接像素点的最大值或最小值点,则标记红色被标记为特征点,如此依次进行,则可以完成图像的特征点提取。
因此在第一步后,我们可以计算出的图1,图2,图3三个DOG图中求图2中是极值的点,如下图所示:
图5:黑色为极小值,白色为极大值
因此,原始图像上以显示的DOG角点检测结果,如下图所示:
参考资料
[1] Difference of Gaussian(DOG) http://fourier.eng.hmc.edu/e161/lectures/gradient/node10.html.
[2] Difference of Gaussian From Wikipedia, the free encyclopedia.
[3] Rafael C.Gonzalez, Rechard E.Woods at. el , "Digital Image Processing Using MatLab (Second Editon)",Gatesamark Publishing.
关于Image Engineering & Computer Vision的更多讨论与交流,敬请关注本博和新浪微博songzi_tea.