杭电1251 统计难题 字典树的应用
题目连接:http://acm.hdu.edu.cn/showproblem.php?pid=1251
初拿到这个题时,感觉是简单的题,想要对单词进行简单的存储,并且在比较时,进行遍历比较,如果数据量很大的话,就需要很长的时间来遍历。进过网上的搜索,我知道了还有字典树的概念,可以对大量的单词进行哈希存储,并且以此存储后,直接遍历一个树的分支就能得到最终的结果,感觉速度能快很多,只是牺牲了很大的内存空间。本代码的写成主要参考网址如下:
http://www.cppblog.com/abilitytao/archive/2009/04/21/80598.aspx
http://zh.wikipedia.org/wiki/Trie
其内容做以简单摘录:
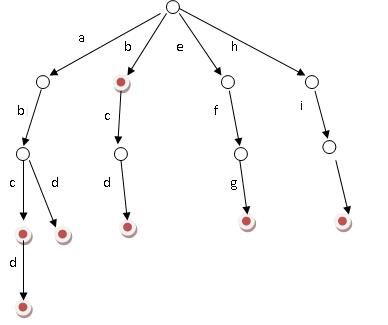
Trie,又称字典树、单词查找树,是一种树形结构,用于保存大量的字符串。它的优点是:利用字符串的公共前缀来节约存储空间。
相对来说,Trie树是一种比较简单的数据结构.理解起来比较简单,正所谓简单的东西也得付出代价.故Trie树也有它的缺点,Trie树的内存消耗非常大.当然,或许用左儿子右兄弟的方法建树的话,可能会好点.
其基本性质可以归纳为:
1. 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。
搜索字典项目的方法为:
(1) 从根结点开始一次搜索;
(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
(3) 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
(4) 迭代过程……
(5) 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
其他操作类似处理.
其他操作类似处理.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 26
typedef struct _node
{
int count;
_node *next[MAX+1];
}node;
static node root = {0, {NULL}};
void insert(char * word, int len)
{
int i;
node *cur, *newnode;
cur = &root;
for(i = 0; i < len; ++i){
if(cur->next[word[i]-'a'] == NULL){
newnode = (node*)malloc(sizeof(node));
memset(newnode, 0, sizeof(node));
newnode->count = 1;
cur->next[word[i]-'a'] = newnode;
}
else{
cur->next[word[i]-'a']->count ++;
}
cur = cur->next[word[i]-'a'];
}
}
node *find(char * wrd, int len)
{
node *cur = &root;
for(int i = 0; i < len; i ++){
if(cur->next[wrd[i]-'a']!=NULL){
cur = cur->next[wrd[i]-'a'];
}
else return NULL;
}
return cur;
}
int main()
{
// freopen("input.txt", "r", stdin);
char *word;
word = (char *)malloc(11*sizeof(char));
while(true){
// word = (char *)malloc(11*sizeof(char));
gets(word);
if(!word[0]){
break;
}
int lenth = strlen(word);
// printf("%d\n",lenth);
insert(word, lenth);
}
node *p;
while(gets(word)){
int lenw = strlen(word);
p = find(word, lenw);
if(p != NULL)printf("%d\n", p->count);
else printf("0\n");
}
return 0;
}