第十周 二叉树遍历思想解决问题

/*
* Copyright (c) 2015, 烟台大学计算机与控制工程学院
* All rights reserved.
* 文件名称： 1.cpp,main.cpp,top.h
* 作者：巩凯强
* 完成日期：2015年12月29日
* 版本号：codeblocks
*
* 问题描述: 实现计算二叉树节点个数，输出所有叶子节点，求二叉树b的叶子节点个数，设计一个算法Level(b,x,h)，返回二叉链b中data值为x的节点的层数，
            判断二叉树是否相似（关于二叉树t1和t2相似的判断：①t1和t2都是空的二叉树，相似；②t1和t2之一为空，另一不为空，则不相似；③t1的左子树和t2的左子树是相似的，且t1的右子树与t2的右子树是相似的，则t1和t2相似。）
* 输入描述： 无
* 程序输出： 见运行结果
*/

程序及代码：

#ifndef BTREE_H_INCLUDED
#define BTREE_H_INCLUDED
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
typedef char ElemType;
typedef struct node
{
    ElemType data;              //数据元素
    struct node *lchild;        //指向左孩子
    struct node *rchild;        //指向右孩子
} BTNode;
void CreateBTNode(BTNode *&b,char *str);        //由str串创建二叉链
int BTNodeDepth(BTNode *b); //求二叉树b的深度
void DispBTNode(BTNode *b); //以括号表示法输出二叉树
void DestroyBTNode(BTNode *&b);  //销毁二叉树
int Nodes(BTNode *b);
void DispLeaf(BTNode *b);
int LeafNodes(BTNode *b);
int Level(BTNode *b,ElemType x,int h);
int Like(BTNode *b1,BTNode *b2);
#endif // BTREE_H_INCLUDED

 

#include "top.h"
void CreateBTNode(BTNode *&b,char *str)     //由str串创建二叉链
{
    BTNode *St[MaxSize],*p=NULL;
    int top=-1,k,j=0;
    char ch;
    b=NULL;             //建立的二叉树初始时为空
    ch=str[j];
    while (ch!='\0')    //str未扫描完时循环
    {
        switch(ch)
        {
        case '(':
            top++;
            St[top]=p;
            k=1;
            break;      //为左节点
        case ')':
            top--;
            break;
        case ',':
            k=2;
            break;                          //为右节点
        default:
            p=(BTNode *)malloc(sizeof(BTNode));
            p->data=ch;
            p->lchild=p->rchild=NULL;
            if (b==NULL)                    //p指向二叉树的根节点
                b=p;
            else                            //已建立二叉树根节点
            {
                switch(k)
                {
                case 1:
                    St[top]->lchild=p;
                    break;
                case 2:
                    St[top]->rchild=p;
                    break;
                }
            }
        }
        j++;
        ch=str[j];
    }
}
void DispBTNode(BTNode *b)  //以括号表示法输出二叉树
{
    if (b!=NULL)
    {
        printf("%c",b->data);
        if (b->lchild!=NULL || b->rchild!=NULL)
        {
            printf("(");
            DispBTNode(b->lchild);
            if (b->rchild!=NULL) printf(",");
            DispBTNode(b->rchild);
            printf(")");
        }
    }
}

void DestroyBTNode(BTNode *&b)   //销毁二叉树
{
    if (b!=NULL)
    {
        DestroyBTNode(b->lchild);
        DestroyBTNode(b->rchild);
        free(b);
    }
}
int Nodes(BTNode *b)
{
    if (b==NULL)
        return 0;
    else
        return Nodes(b->lchild)+Nodes(b->rchild)+1;
}
void DispLeaf(BTNode *b)
{
    if (b!=NULL)
    {
        if (b->lchild==NULL && b->rchild==NULL)
            printf("%c ",b->data);
        else
        {
            DispLeaf(b->lchild);
            DispLeaf(b->rchild);
        }
    }
}
int LeafNodes(BTNode *b)    //求二叉树b的叶子节点个数
{
    int num1,num2;
    if (b==NULL)
        return 0;
    else if (b->lchild==NULL && b->rchild==NULL)
        return 1;
    else
    {
        num1=LeafNodes(b->lchild);
        num2=LeafNodes(b->rchild);
        return (num1+num2);
    }
}
int Level(BTNode *b,ElemType x,int h)
{
    int l;
    if (b==NULL)
        return 0;
    else if (b->data==x)
        return h;
    else
    {
        l=Level(b->lchild,x,h+1);
        if (l==0)
            return Level(b->rchild,x,h+1);
        else
            return l;
    }
}
int Like(BTNode *b1,BTNode *b2)
{
    int like1,like2;
    if (b1==NULL && b2==NULL)
        return 1;
    else if (b1==NULL || b2==NULL)
        return 0;
    else
    {
        like1=Like(b1->lchild,b2->lchild);
        like2=Like(b1->rchild,b2->rchild);
        return (like1 & like2);
    }
}

#include"top.h"
int main()
{
    BTNode *b,*b1, *b2, *b3;
    CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    printf("二叉树节点个数: %d\n", Nodes(b));
    DestroyBTNode(b);

    CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    printf("二叉树中所有的叶子节点是: ");
    DispLeaf(b);
    printf("\n");
    DestroyBTNode(b);

    CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    printf("二叉树b的叶子节点个数: %d\n",LeafNodes(b));
    DestroyBTNode(b);

    CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    printf("值为\'K\'的节点在二叉树中出现在第 %d 层上n",Level(b,'K',1));
    DestroyBTNode(b);

    CreateBTNode(b1,"B(D,E(H(J,K(L,M(,N)))))");
    CreateBTNode(b2,"A(B(D(,G)),C(E,F))");
    CreateBTNode(b3,"u(v(w(,x)),y(z,p))");
    if(Like(b1, b2))
        printf("b1和b2相似\n");
    else
        printf("b1和b2不相似\n");
    if(Like(b2, b3))
        printf("b2和b3相似\n");
    else
        printf("b2和b3不相似\n");
    DestroyBTNode(b1);
    DestroyBTNode(b2);
    DestroyBTNode(b3);
    return 0;
}

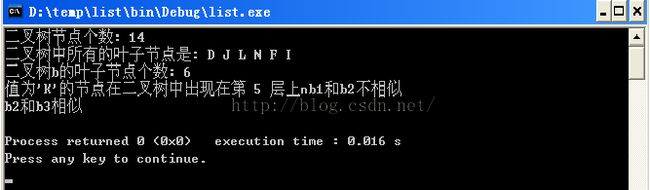
运行结果：

知识点总结：

          实现计算二叉树节点个数，输出所有叶子节点，求二叉树b的叶子节点个数，设计一个算法Level(b,x,h)，返回二叉链b中data值为x的节点的层数， 判断二叉树是否相似（关于二叉树t1和t2相似的判断：①t1和t2都是空的二叉树，相似；②t1和t2之一为空，另一不为空，则不相似；③t1的左子树和t2的左子树是相似的，且t1的右子树与t2的右子树是相似的，则t1和t2相似。）

学习心得：

         通过自己学习的知识来解决实际生活中遇到的问题。