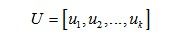PCA 的具体实现 (Eigenfaces特征脸)
特征脸技术是近期发展起来的用于人脸或者一般性刚体识别以及其它涉及到人脸处理的一种方法。首先把一批人脸图像转换成一个特征向量集,称为“Eigenfaces”,即“特征脸”,它们是最初训练图像集的基本组件。识别的过程是把一副新的图像投影到特征脸子空间,并通过它的投影点在子空间的位置以及投影线的长度来进行判定和识别。
原始图像投影到该特征空间中。特别说明,此时的原始图像x存成大小是n维的向量,即:
(3-1)
训练集为(这里p为样本图像数量),形成矩阵X[n][p],其中行代表像元,列代表每幅人脸图像。
将训练样本集中的人脸图像减去平均人脸图像,计算离散差值,将训练图像中心化。
将中心化之后图像组成一个大小为n×p的矩阵X:
(3-3)
将中心化后的图像组成的矩阵X乘以它的转置矩阵得到协方差矩阵Ω:
求解协方差矩阵Ω的k个非零特征值,以及所对应的特征向量,一般来说,训练图像数量p远远小于一幅图像的像素值n,所以协方差矩阵Ω最多有对应于非零特征值的p个特征向量,所以k≤p.按照特征值的从大到小的顺序排列特征向量,对应于最大特征值的特征向量反应了训练图像间的最大差异,而对应的特征值越小的特征向量,反应的图像间的差异越小。所有的非零特征值对应的特征向量,组成特征空间,也就是所谓的“特征脸”空间。
![]() 计算特征值和特征向量,其中U为对应于特征值的特征向集。排列特征向量:按照非零特征值,从大到小的顺序,将对应的特征向量排列。所组成的特征向量矩阵即为特征空间U,U的每一列为一个特征向量:
计算特征值和特征向量,其中U为对应于特征值的特征向集。排列特征向量:按照非零特征值,从大到小的顺序,将对应的特征向量排列。所组成的特征向量矩阵即为特征空间U,U的每一列为一个特征向量:
这样每一幅人脸图像都可以投影到由张成的子空间中。因此每一幅人脸图像对应于子空间中的一个点,同样,子空间中的每个点对应于一幅图像,图3-2显示的是
所对应的图像,由于这些图像很像人脸,所以它们被称为“特征脸”。
图3-2 特征脸
训练图像投影得到特征脸子空间
有了这样一个由“特征脸”组成的降维特征子空间,任何一幅中心化后的人脸图像都可以通过下面的式子投影到特征脸子空间并获得一组坐标系数:
(3 - 6)