Farey序列（Stern-Brocot tree的衍生）

       早在一百多的年前，人们就发现了Farey序列，它是介于0和1之间满足一定的性质的一个有理数列。但一直到近代才被得到真正的应用，特别是在近代数论中，也逐渐受到人们的重视。这里对于这个序列的性质进行了初步探讨研究，并根据这个性质得到关于有理数和无理数一些有趣的命题。

网上找到的一段描述，学习一下。

Farey序列

Fn = {a/b | gcd(a,b)=1 && 0<=a,b<=n};

即由小于或等于n的整数所组成的不可再约分数的递增序列，并满足分子分母互质。

如：

F1 = {0/1, 1/1}

F2 = {0/1, 1/2, 1/1}

F3 = {0/1, 1/3, 1/2, 2/3, 1/1}

性质

除了F1，其余Farey序列都有奇数个元素，并且中间值是1/2。

Farey序列是一个对称序列，头尾之和为1。

假如序列中有三个连续元素x1/y1, x2/y2, x3/y3，则有x2 = x1+x3; y2 = y1+y3;

并且有x1*y2 – x2*y1 = 1。这条性质保证构造出来的分式肯定是不可约分式。

构造

从第三个性质我们可以得出它的构造方法。

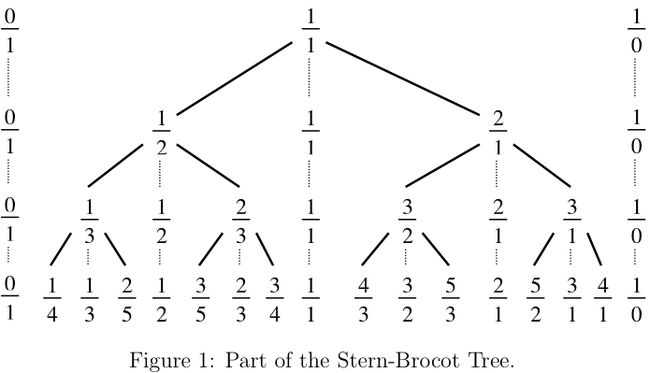
如图即是一棵Stern-Brocot tree。

第N排的真分数部分即为N阶Farey序。

1.对于每次在m1/n1,m2/n2中插入(m1+m2)/(n1+n2)构成下一排。

2.对于任意一个Farey序中连续的分数m1/n1,m2/n2，必有m1/n1<m2/n2。

3.Stern-Brocot树可以构成所有有理数。

4.Stern-Brocot树构成的所有分数均为最简分数，即gcd(m,n)==1。

5.任意两个构造时相邻的两个分数都满足m1n2-m2n1==1。

二．N阶Farey序列的构造。

1.递归构造。

依靠m1/n1, (m1+m2)/(n1+n2),m2/n2的法则递归构造。

Inline void Build(int m1,int n1,int m2,int n2){

  If (m1+m2>N||n1+n2>N) return;

  Build(m1,n1,m1+m2,n1+n2);

  Sta[++top].a=m1+m2;

  Sta[++top].b=n1+n2;

  Build(m1+m2,n1+n2,m2,n2);

}

时间复杂度O(N^2)，空间复杂度O(N)

2.非递归构造。

对于任意N阶Farey序列中连续的三个分数m1/n1,m2/n2,m3/n3,必有：

  m3=[(n1+N)/n2]m2-m1

  n3=[(n1+N)/n2]n2-n1;

  注：[a]表示a向下取整。

证明：

  由于这三个分数在该序列中连续存在，所以n1+n2>N,m1+m2>N。

 N=((n1+N)/n2)n2-n1>=n3>N-n2=((n1+N)/n2-1)n2-n1n3=[(n1+N)/n2]n2-n

     又n2m3-m2n3=1，

得  m3=(m2n3+1)/n2=(([(n1+N)/n2]n2-n1)m2+1)/n2

       所以m3=[(n1+N)/n2]m2-(n1m2-1)/n2=[(n1+N)/n2]m2-m1

     得证。

三．    求N阶Farey序列的第k个最小分数。

1. 按照递归构造方法，构造Stern-Brocot树，适用于要求求出1阶2阶...N阶。

注意，当N过大时，需要手写模拟栈完成。

2.按照非递归构造方法，第一项是0/1,第二项是1/N,然后递推构造，适用于单求第N阶Farey序列。