计算几何基础——矢量和叉积 && 叉积、线段相交判断、凸包（转载）

计算几何基础——矢量和叉积 && 叉积、线段相交判断、凸包

矢量

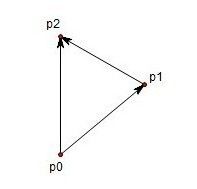
  如果一条线段的端点是有次序之分的话，那么这种线段就称为 有向线段，如果有向线段p1p2的起点p1在坐标的原点，则可以把它称为矢量 p2。

矢量的加减

      设二维矢量 P = (x1, y1), Q = (x2, y2)，则 P + Q = (x1 + x2, y1 + y2), P - Q = (x1 - x2, y1 - y2)，且有 P + Q = Q + P, P - Q = -(Q - P)。

矢量叉积

      设矢量 P = (x1, y1), Q = (x2, y2)，则 P * Q = x1 * y2 - x2 * y1; 其结果是一个由 (0, 0), P, Q, P + Q 所组成的平行四边形的 带符号的面积，P * Q = -(Q * P), P * (- Q) = -(P * Q)。

      叉积的一个非常重要的性质是可以通过它的符号来判断两矢量相互之间的顺逆时针关系：

            若 P * Q > 0，则 P 在 Q 的顺时针方向；

            若 P * Q < 0, 则 P 在 Q 的逆时针方向；

            若 P * Q = 0，则 P 与 Q 共线，但不确定 P, Q 的方向是否相同；

折线段的拐向判断

  如图，假设有折线段 p0p1p2 ，要确定 p1p2 相对于 p0p1 是向左拐还是向右拐，可以通过计算(p2 - p0)*(p1 - p0) 的符号来确定折线的拐向（点 p2 - p0 实际上就是向量 p2，但这里要注意线段和矢量的区别）。

判断点是否在线段上

  设点 Q = (x, y), P1 = (x1, y1), P2 = (x2, y2)，若 (Q - P1)*(P2 - P1) = 0 且 min(x1, x2) <= x <= max(x1, x2) && min(y1, y2) <= y <= max(y1, y2)，则点 Q 在线段 P1P2 上。

判断两线段是否相交

1）快速排斥试验

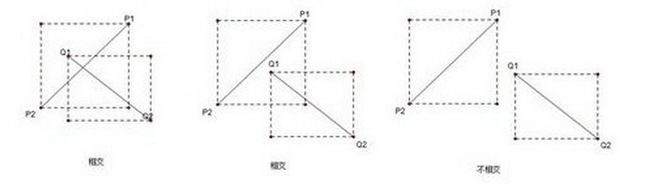
       设以线段 P1P2 为对角线的矩形为 R，设以线段 Q1Q2 为对角线的矩形为 T，若 R、T 不相交，则两线段不可能相交。

       假设 P1 = (x1, y1), P2 = (x2, y2), Q1 = (x3, y3), Q2 = (x4, y4)，设矩形 R 的 x 坐标的最小边界为 minRX = min(x1, x2)，以此类推，将矩形表示为 R = (minRX, minRY, maxRX, maxRY) 的形式，若两矩形相交，则相交的部分构成了一个新的矩形 F，如图所示，我们可以知道 F 的 minFX = max(minRX, minTX), minFY = max(minRY, minTY), maxFX = min(maxRX, maxTX), maxFY = min(maxRY, maxTX)，得到 F 的各个值之后，只要判断矩形 F 是否成立就知道 R 和 T 到底有没有相交了，若 minFX > maxFX 或 minFY > maxFy 则 F 无法构成，RT不相交，否则 RT相交。

2）跨立试验

         若 P1P2 跨立 Q1Q2，则 P1,P2 分别在 Q1Q2 所在直线的两端，则有 (P1 - Q1)*(Q2 - Q1) * (Q2 - Q1)*(P2 - Q1) > 0，当 (P1 - Q1)*(Q2 - Q1) = 0 时，说明 (P1 - Q1) 与 (Q2 - Q1) 共线，但由于已经经过快速排斥试验，所以 Q1 必为 P1P2 与 Q1Q2 的交点，依然满足线段相交的条件，则跨立试验可改为：

       当 (P1 - Q1)*(Q2 - Q1) * (Q2 - Q1)*(P2 - Q1) >= 0，则 P1P2 跨立 Q1Q2，当 Q1Q2 也跨立 P1P2 的时候，则 P1P2 相交。

      （注意式子中被隔开的 * 代表两个叉积的值的相乘，而另外的两个 * 则代表计算矢量叉积）。

 

一、叉积

   叉积的计算是线段方法的核心。对于向来p1和p2，叉积是由点(0,0)、p1、p2和p1+p2构成的平行四边形的有向面积。另一种与之等价但更有效的的叉积定义方式是将其看做矩阵行列式：

p1×p2 = x1y2 - x2y1 = - p2×p1

若p1×p2为正，则相对于原点(0,0)来说，p1位于p2顺时针方向；若p1×p2为负，p1位于p2逆时针方向；若为0则方向相同，或相反。

      若是相对于点p0(x0,y0)而非原点，则p0p1和p0p2的叉积为(p1-p0)×(p2-p0) = (x1-x0)(y2-y0)-(x2-x0)(y1-y0)。 

      确定连续线段是向左转还是向右转

对于线段p0p1和p1p2，采用叉积可以避免计算角度，只需简单的计算一下p0p2是位于p0p1的顺时针还是逆时针方向。计算叉积

(p2-p0)×(p1-p0) = (x2-x0)(y1-y0) - (x1-x0)(y2-y0)。

     若结果为负，p0p2在p0p1的逆时针方向，在p1处左转；结果为正则右转；为0表示三点共线。

 

判断两条线段是否相交

要判断两条线段是否相交，则需要检查每条线段是否跨越了另一条线段的直线。如果点p1位于某直线的一边，而点p2位于该直线的另一边，则称p1p2跨越了这条直线。两条线段相交，当且仅当下面两个条件至少成立一个：

1. 每条线段都跨越了包含另一条线段的直线

2. 一条线段的一个端点落在另一条线段上

 

二、确定任意一对线段是否相交

   给定一个线段的集合，仅仅判断是否有两个线段相交，不必输出所有相交的线段对。此处我们假设，线段均不垂直。

我们使用“扫除”算法来解决这个问题。在扫除过程中，一条假想的扫除线穿过一个给定的几何物体集合，会与集合中的部分线段相交。下图中扫除线r与线段a、c相交，且与a的交点的y坐标值大于c的，则认为此处a>c。

  在图(a)中，在r处，a>c；在t处，a还是>c，那么我们认为a和c没有相交。而在图(b)中，在v处，e>f，而在图w处，f>e，故e和f相交。

 

  上图描述了一个算法，我们按照线段端点的x坐标，从小到达，进行“扫除”。当在一个线段的左端点扫除时，将所有相交的线段序列按序放入一个“完全前序关系T”中。当扫到线段的右端点时，从T中去除该线段。但是，如果位于在该线段上方的线段集合，与位于该线段下方的线段集合有交集，则表明有线段相交。

 

关键在于，如果存储T，如果求交集。可以用红黑树来存储T。

算法步骤

1. 初始化T为空集

2. 对线段的端点排序

3. 在端点p处，开始扫除，从最左边的处开始

     如果p是线段s的左端点

    Insert(T, s);

       如果有线段在扫除线处相交

         return true;

 如果p是线段的右端点

    如果above(T, s) 和 below(T, s)有交集，则

       return true;//即线段集中存在线段相交

     无交集则，Delete(T, s);

4. return false

 

三、寻找凸包

     点集Q的凸包，是一个最小的凸多边形P，满足Q中的每个点都在P的边界上，或者在P的内部。

 

Graham扫描法: 复杂度O(nlogn)

1. 选取y最小的点，多个y最小的话，选取其中x最小的点，作为p0；
   

2. 剩余的点，按照p0和pi的极角的逆时针排序，编号为p1,p2,...,pm；

3. 如果m小于2，表示点数小于3，形不成多边形；

4. 设定以空栈S，将p0、p1、p2压入栈中；

5. for i=3 to m

   1. 得到栈顶的2个点pi-1和pi-2，如果t1t0向t0pi转的时候，不是左转，就把顶点t0出栈；

   2. 如果出栈了t0，就继续a，直到栈的顶点不再出栈位置；

   3. 将pi入栈。

6. return S

图中，从a到f是一步一步选择的过程。

Jarvis步进法：复杂度O(nh)，h是凸包顶点数

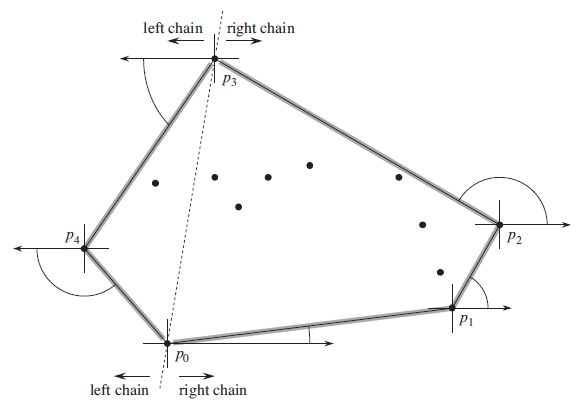
  先找到最下边结点里最左边的点p0，然后寻找使得p0p1极角最小的点，则p1也是凸包顶点；继续寻找使得p1p2极角最小的点，直到达到最高点pk，上图是p3，此时已经构造好了CH(Q)的右链。为了构造左链，寻找pk+1使得pkpk+1极角最小，但此时x轴啊原x轴的负方向。

除此之外，还有增量法、分治法、剪枝-搜索方法，其中剪枝-搜索方法复杂度为O(nlgh)。