聚类

http://blog.csdn.net/bendanban/article/details/17844831

聚类clustering，无监督学习unsupervised learning分类也。 聚类有不少经典的方法，我们先从基本概念，本质属性开始讨论，慢慢把这些方法掌握，应用到实际问题中。

1、基本概念。

  既然要把给出的特征向量分成不同的类里，我们首先应该想到的是，什么是类(cluster或者group)？ 在研究过程中大家不断的给出一些定义， 但是都比较模糊和宽泛，很难找到一个大家都容易接受的定义，最近的一个，差不多大家都比较认同的定义是这样描述的。

"continuous regions of this space containing a relatively high density of points, separated from other high density regions by regions of relatively low density of points"

this space 是指特征向量空间，每个特征向量被看成空间中的一个点。

什么是聚类呢？ 

我们需要聚类的数据集是：X = {x_1, ..., x_N}， 表示有N个特征向量需要聚类。

定义X的m聚类，就是将X分成m组向量，每一组类用C表示，C_1, ..., C_m

其中 C_i != 空集； C的并是X； 任意两个类的交集是空集。在同一个类中的特征向量是相似的（similar），不同类中的特征向量不相似（dissimilar），量化这两个词有点困难，可能需要根据你的实际情况来定义相似性和不相似性。 

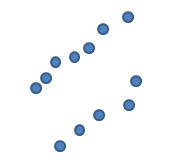
大约有三种不同的类别，如下图

图1， Compact Cluster

图 2， Elongated clusters

图3、 Spherical and ellipsoidal clusters

这三种不同的cluster类型，对相似度的量化有所差异。

前面描述的这种聚类方式一般称之为硬聚类（hard 或者 crisp）

还有一种方式是软聚类，就是说每个特征属于某个类有一个隶属度来表述它，比如x属于C_1的隶属度为0.2， 属于C_2的隶属度为0.8 ，对于两类的情况，这样是合理的。

2、 关于proximity measure

之前写这篇博文的时候，不想写这部分，现在觉得还是写写的好啊，保证知识的完整性，多多思考还是好的。

我们可以用 相似度(similarity)或不相似度(dissimilarity) 来量化两个特征向量、特征向量与一组特征向量以及两组特征向量之间的proximity。

多数人认为两个向量的proximity测度是最基础的，proximity就翻译成近邻吧。

什么是相似度？定义两个向量之间的相似度，它是一个函数，满足如下规则：

   * 相似度函数与特征向量的输入顺序无关。 s(v1, v2) = s(v2, v1)

   * 任意的同一个特征向量的相似度取得最大值。 s(v,v) 取得相似度函数的值域中的最大值。并且当且仅当输入向量相同的时候，才能取得这个最大值。

   * 还有一个不等式需要满足： s(x,y) s(y,z) <= [s(x,y)+s(y,z)]s(x,z), for all x,y,z in X

什么是不相似度？ 也用函数定义，也满足一下规则：

   * 当且仅当两个输入向量相同时，不相似度函数取到最小值，就是说只有这个时候，两个向量才最不不相似，就是最相似。

   * 不相似度函数的值与输入顺序无关。

   * 满足三角不等式。 d(x,z) <= d(x,y) + d(y,z) , 对任意 x，y，z in X都成立。