后缀数组学习笔记

1、基本定义

子串：字符串S的子串r[i..j]，i<=j,表示r串中从i到是j这一段，也就是顺次排列r[i], r[i+1],...,r[j]形成的字符串

后缀：是指从某个位置i开始到整个串尾结束的一个特殊子串。字符串r的从第i个字符开始的后缀表示为suffix(i)，也就是suffix(i)=r[i..len(r)]

大小比较：关于字符串的大小 比较，是指通常所说的”字典顺序“比较，也就是对于两个字符串u,v，令i从开始顺次比较u[i]和v[i]，如果u[i]=v[i]，则令i加1，否则若u[i] < v[i]，则认为u < v,u[i] > v[i]则认为u > v，比较结束。如果i > len(u)或者i > len(v)仍比较不出结果，那么若len(u)<len(v)则认为u<v,若len(u) = len(v)则认为u=v,若len(u)>len(v)则u>v

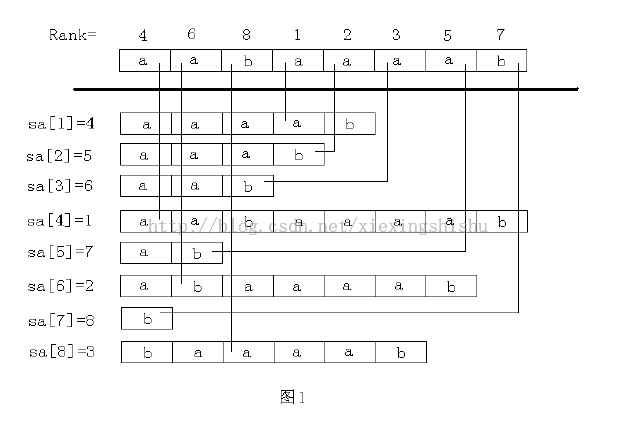
后缀数组：sa是一个一维数组，它保存1..n的某个排列sa[1],sa[2],....,sa[n],并且保证suffix(sa[i]) < suffix(sa[i+1], 1 <= i < n。也就是说将s的n个后缀从小到大进行排序后把排好序的后缀的开头位置顺次放入sa中。

名次数组：名次数组rank[i]保存的是suffix(i)在所有后缀中从小到大排列的名次

设字符串的长度为n。为了方便比较大小 ，可以在字符串后面添加一个字符，这个字符没有在前面的字符中出现过，而且比前面的字符都要小。在求出名次数组后，可以用o(1)的时间比较任意两个后缀的大小 。在求出后缀数组或名次数组中的其中一个后，可以用o(n)的时间求出另外一个。

2、倍增算法

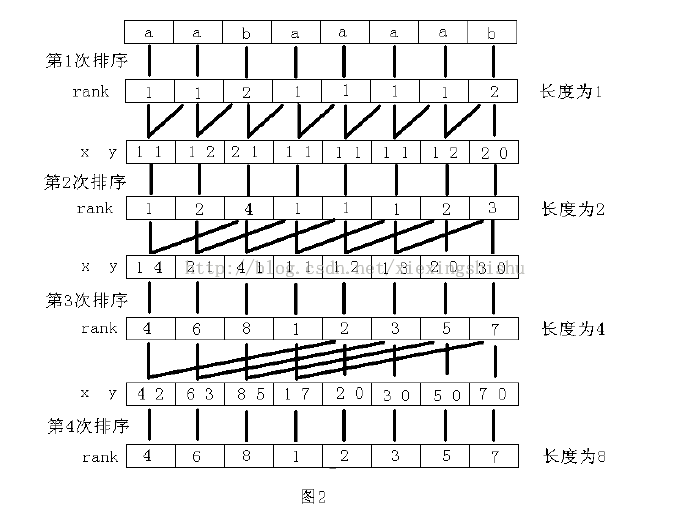
其主要思路是：用倍增的方法对每个字符开始的长度为2的k次幂的子字符串进行排序，求出排名，即rank值，k从0开始，每次加1，当2的k次幂大于n以后，每个字符开始的升序为2的k次幂的子字符串便相当于所有的后缀。并且这些子字符串都一定已经比较出大小，即rank值中没有相同的值，那么此时rank值就是最后的结构。第一次排序都利用上次长度为2的k-1次幂的字符串的rank值，那么长度为2的k交幂的字符串就可以用两个长度为2的k-1次幂的字符中的排名作为关键字表示，然后进行基数排序，便得出了长度为2的k次幂的字符串的rank值。以字符串"aabaaaab"为例，x,y表示长度为2的k次幂的字符串的两个关键字

其时间复杂度为O(nlgn),代码为：

const int MAXN = 660;

char s[MAXN];
int sa[MAXN], t[MAXN], t2[MAXN], c[MAXN];

void build_sa(int n, int m)
{
    int *x = t, *y = t2;

    for (int i = 0; i < m; i++) c[i] = 0;
    for (int i = 0; i < n; i++) c[x[i] = s[i]]++;
    for (int i = 1; i < m; i++) c[i] += c[i - 1];
    for (int i = n - 1; i >= 0; i--) sa[--c[x[i]]] = i;

    for (int k = 1; k <= n; k <<= 1) {
        int p = 0;
        for (int i = n - k; i < n; i++) y[p++] = i;
        for (int i = 0; i < n; i++) if (sa[i] >= k) y[p++] = sa[i] - k;
        for (int i = 0; i < m; i++) c[i] = 0;
        for (int i = 0; i < n; i++) c[x[y[i]]]++;
        for (int i = 1; i < m; i++) c[i] += c[i - 1];
        for (int i = n - 1; i >= 0; i--) sa[--c[x[y[i]]]] = y[i];

        swap(x, y);
        p = 1;
        x[sa[0]] = 0;

        for (int i = 1; i < n; i++) {
            x[sa[i]] = (y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k] ? p - 1 : p++);
        }

        if (p >= n) break;
        m = p;
    }
}

3、最长公共前缀（LCP）

height数组：定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。那么对于j和k，不妨设rank[j]<rank[k],则有以下性质：

后缀j和k的LCP长度等于height[rank[j] + 1],height[rank[j] + 2],......,height[rank[k]]的最小值

定义h[i]=height[rank[i]]，也就是suffix(i)和在它前一名的后缀的最长公共前缀，h数组有如下性质:h[i] >= h[i - 1] - 1

其实现如下：

int Rank[MAXN], height[MAXN];

void getHeight(int n)
{
    for (int i = 0; i < n; i++) Rank[sa[i]] = i;
    int k = 0;

    for (int i = 0; i < n; i++) {
        if (k > 0) k--;
        else k = 0;
        int j = sa[Rank[i] - 1];
        while (s[i + k] == s[j + k]) k++;
        height[Rank[i]] = k;
    }
}