倍增算法的另一种解法

网上一搜索倍增算法，基本就是罗穗骞同学的介绍。这同学高中时期就研究这么深入，让我这研究生毕业的人汗颜，慢慢爬坑吧。不过说实在的，这代码写的实在看着有点费劲。网上又有人整理了下。不过我看的还是一头雾水，希望有明白人能说明一下。要想了解倍增算法，最好先对RMQ和基数排序算法有一定了解，还要了解一下后缀数组。下面把代码贴过来。

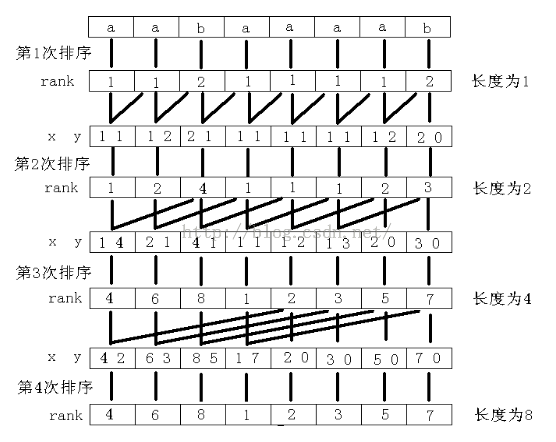
例子图如下：

但是代码的实现和这个图出入很大，不好理解。

/*
* 字符串转化成了字符的ASCII码整数表示
* sa[i]=j;表示排在第i位的后缀数组是第j个。这个j是后缀数组在原字符串中的位置，也就是y数组的含义
*/
void radix_sort(int n, int sz)
{
	memset(cnt, 0, sizeof(cnt));
	for (int i = 0;i<n;i++)
		cnt[x[y[i]]]++;
	for (int i = 1;i<sz;i++)
		cnt[i] += cnt[i - 1];
	for (int i = n - 1;i >= 0;i--)
		sa[--cnt[x[y[i]]]] = y[i];
}

/*
* rank[i]：表示当前某一时刻后缀数组的排序，没swap之前x指向它.
* sz ：当前最大rank值.
* y: 以第2关键字比较时，text[]的排序位置
*/
void get_sa(char text[], int n, int sz = 128)
{
	x = rank, y = rank2;
	for (int i = 0;i<n;i++)
		x[i] = text[i], \
		y[i] = i;
	radix_sort(n, sz);
	for (int len = 1;len<n;len <<= 1)
	{
		int yIdx = 0;
		for (int i = n - len;i<n;i++)	//看例子图就知道了，len=1时，y数组最后一个元素是0，因为没有和他倍增的。
			y[yIdx++] = i;				//第二位是0的肯定是最小的，直接放前面
		for (int i = 0;i < n;i++) {
			if (sa[i] >= len)			
				y[yIdx++] = sa[i] - len;//减掉上面直接放前面的那些len个字符串
		}
		radix_sort(n, sz);
		swap(x, y);
		x[sa[0]] = yIdx = 0;
		for (int i = 1;i<n;i++)
		{
			//这块看的稀里糊涂，不知道下面说的对不对：
			//要记住sa[i]的含义：当前排在第i位的后缀数组(用在原串中的位置表示).
			//下一步的倍增就是分别从sa[i]和sa[i]+len开始的，长度为len的两个数组的倍增。
			//如果这两处字符分别和前一后缀数组的两处字符相等，表示这两后缀还没有区分开，rank值相同。这块说的自己都不明白...仅仅根据字符就能区分字符串？
			if (y[sa[i - 1]] == y[sa[i]] && sa[i - 1] + len<n && sa[i] + len<n &&  y[sa[i - 1] + len] == y[sa[i] + len])
				x[sa[i]] = yIdx;
			else
				x[sa[i]] = ++yIdx;
		}
		sz = yIdx + 1;
		if (sz >= n)
			break;
	}
	for (int i = 0;i<n;i++)
		rank[i] = x[i];
}

void get_height(char text[], int n)
{
	int k = 0;
	for (int i = 0;i<n;i++)
	{
		if (rank[i] == 0)
			continue;
		k = max(0, k - 1);
		int j = sa[rank[i] - 1];
		while (i + k<n && j + k<n && text[i + k] == text[j + k])
			k++;
		height[rank[i]] = k;
	}
}

上面求height数组，罗同学的代码也很不错，外加网友注释，一并贴过来。

//能够线性计算height[]的值的关键在于h[](height[rank[]])的性质，即h[i]>=h[i-1]-1，下面具体分析一下这个不等式的由来。
//论文里面证明的部分一开始看得我云里雾里，后来画了一下终于搞明白了，我们先把要证什么放在这：对于第i个后缀，设j=sa[rank[i] - 1]，也就是说j是i的按排名来的上一个字符串，按定义来i和j的最长公共前缀就是height[rank[i]]，我们现在就是想知道height[rank[i]]至少是多少，而我们要证明的就是至少是height[rank[i-1]]-1。
//好啦，现在开始证吧。
//首先我们不妨设第i-1个字符串（这里以及后面指的“第?个字符串”不是按字典序排名来的，是按照首字符在字符串中的位置来的）按字典序排名来的前面的那个字符串是第k个字符串，注意k不一定是i-2，因为第k个字符串是按字典序排名来的i-1前面那个，并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。
//这时，依据height[]的定义，第k个字符串和第i-1个字符串的公共前缀自然是height[rank[i-1]]，现在先讨论一下第k+1个字符串和第i个字符串的关系。
//第一种情况，第k个字符串和第i-1个字符串的首字符不同，那么第k+1个字符串的排名既可能在i的前面，也可能在i的后面，但没有关系，因为height[rank[i-1]]就是0了呀，那么无论height[rank[i]]是多少都会有height[rank[i]]>=height[rank[i-1]]-1，也就是h[i]>=h[i-1]-1。
//第二种情况，第k个字符串和第i-1个字符串的首字符相同，那么由于第k+1个字符串就是第k个字符串去掉首字符得到的，第i个字符串也是第i-1个字符串去掉首字符得到的，那么显然第k+1个字符串要排在第i个字符串前面，要么就产生矛盾了。同时，第k个字符串和第i-1个字符串的最长公共前缀是height[rank[i-1]]，那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rank[i-1]]-1。
//到此为止，第二种情况的证明还没有完，我们可以试想一下，对于比第i个字符串的字典序排名更靠前的那些字符串，谁和第i个字符串的相似度最高（这里说的相似度是指最长公共前缀的长度）？显然是排名紧邻第i个字符串的那个字符串了呀，即sa[rank[i]-1]。也就是说sa[rank[i]]和sa[rank[i]-1]的最长公共前缀至少是height[rank[i-1]]-1，那么就有height[rank[i]]>=height[rank[i-1]]-1，也即h[i]>=h[i-1]-1。
//证明完这些之后，下面的代码也就比较容易看懂了。
int rank[maxn],height[maxn];
void calheight(int *r,int *sa,int n)
{
    int i,j,k=0;
    for(i=1;i<=n;i++) rank[sa[i]]=i;  //计算每个字符串的字典序排名
    for(i=0;i<n;height[rank[i++]]=k)  //将计算出来的height[rank[i]]的值，也就是k，赋给height[rank[i]]。i是由0循环到n-1，但实际上height[]计算的顺序是由height[rank[0]]计算到height[rank[n-1]]。
    for(k?k--:0,j=sa[rank[i]-1];r[i+k]==r[j+k];k++);  //上一次的计算结果是k，首先判断一下如果k是0的话，那么k就不用动了，从首字符开始看第i个字符串和第j个字符串前面有多少是相同的，如果k不为0，按我们前面证明的，最长公共前缀的长度至少是k-1，于是从首字符后面k-1个字符开始检查起即可。
    return;
}

我自己实现了一种做法，倒是完全按照图示的思想来求解，但用的是二叉排序树(BST)来求解rank数组，而不是基数排序。空间复杂度要高一些，时间复杂度因为有内存申请释放，也不是很好。方法倒是可行，很简单直观，不知道是否违背了倍增算法的思想。算了，权当练手吧，上面的代码看了好几天，实在是看的累了，翻篇。

typedef struct node {
	node * left;
	node * right;
	int	 data;
}Node;
std::map<int, int> mapIdx;
Node *root= NULL;
int xy[N];
int idx = 0;
void insert(Node *&tree, int num)
{
	if (tree == NULL) {
		Node* t = new Node;
		t->data = num;
		t->left = t->right = NULL;
		tree = t;
		return;
	}

	if (tree->data > num)
		insert(tree->left, num);
	else if (tree->data < num)
		insert(tree->right, num);
}
void create(int text[], int len)
{
	for (int i = 0; i < len;++i)
	{
		insert(root, text[i]);
	}
}
void InOderTranverse(Node *node)
{
	if (!node)	return;
	if (node->left)
		InOderTranverse(node->left);
	mapIdx[node->data] = ++idx;
	if (node->right)
		InOderTranverse(node->right);
	delete node;
}
void DA(int xy[], int n)
{
	for (int len = 1;len < n;len <<= 1)
	{
		create(xy, n);
		InOderTranverse(root);
		for (int i = 0;i < n; ++i)
			rank[i] = mapIdx[xy[i]];
		if (mapIdx.size() == n)
			return;
		root = NULL;
		idx = 0;
		mapIdx.clear();
		for (int i = 0;i < n;i++)
		{
			if (i + len < n)
				xy[i] = rank[i]*10 + rank[i+len];
			else
				xy[i] = rank[i] * 10;
		}
	}
}