简单易学的机器学习算法——集成方法(Ensemble Method)
一、集成学习方法的思想
前面介绍了一系列的算法,每个算法有不同的适用范围,例如有处理线性可分问题的,有处理线性不可分问题。在现实世界的生活中,常常会因为“集体智慧”使得问题被很容易解决,那么问题来了,在机器学习问题中,对于一个复杂的任务来说,能否将很多的机器学习算法组合在一起,这样计算出来的结果会不会比使用单一的算法性能更好?这样的思路就是集成学习方法。
集成学习方法是指组合多个模型,以获得更好的效果,使集成的模型具有更强的泛化能力。对于多个模型,如何组合这些模型,主要有以下几种不同的方法:
- 在验证数据集上上找到表现最好的模型作为最终的预测模型;
- 对多个模型的预测结果进行投票或者取平均值;
- 对多个模型的预测结果做加权平均。
二、集成学习的主要方法
1、强可学习和弱可学习
在集成学习方法中,是将多个弱模型,通过一定的组合方式,组合成一个强模型。在《统计学习方法》中介绍了“强可学习
(strongly learnable)
”和“弱可学习
(weakly learnable)
”的概念。
在概率近似正确
(probably approximately correct, PAC)
学习的框架中,一个概念(一个类),如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么就称这个概念是强可学习的。一个概念,如果存在一个多项式的学习算法能够学习它,学习正确率仅比随机猜测略好,那么就称这个概念是弱可学习的。
Schapire
指出在
PAC
学习框架下,一个概念是强可学习的充分必要条件是这个概念是弱可学习的。那么对于一个学习问题,若是找到“弱学习算法”,那么可以将弱学习方法变成“强学习算法”。
2、在验证集上找表现最好的模型
这样的方法的思想与决策树的思想类似,在不同的条件下选择满足条件的算法。
3、多个模型投票或者取平均值
对于数据集训练多个模型,对于分类问题,可以采用投票的方法,选择票数最多的类别作为最终的类别,而对于回归问题,可以采用取均值的方法,取得的均值作为最终的结果。在这样的思路里最著名的是
Bagging
方法.
Bagging
即
Boostrap Aggregating
,其中,
Boostrap
是一种有放回的抽样方法,其抽样策略是简单的随机抽样。
在
Bagging
方法中,让学习算法训练多次,每次的训练集由初始的训练集中随机取出的 个训练样本组成,初始的训练样本在某次的训练集中可能出现多次或者根本不出现。最终训练出
个训练样本组成,初始的训练样本在某次的训练集中可能出现多次或者根本不出现。最终训练出 个预测函数
个预测函数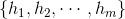 ,最终的预测函数为对于分类和回归问题可采用如下的两种方法:
,最终的预测函数为对于分类和回归问题可采用如下的两种方法:
随机森林算法就是基于
Bagging
思想的学习算法。
4、对多个模型的预测结果做加权平均
在上述的
Bagging
方法中,其特点在于随机化抽样,通过反复的抽样训练新的模型,最终在这些模型的基础上取平均。而在对多个模型的预测结果做加权平均则是将多个弱学习模型提升为强学习模型,这就是
Boosting
的核心思想。
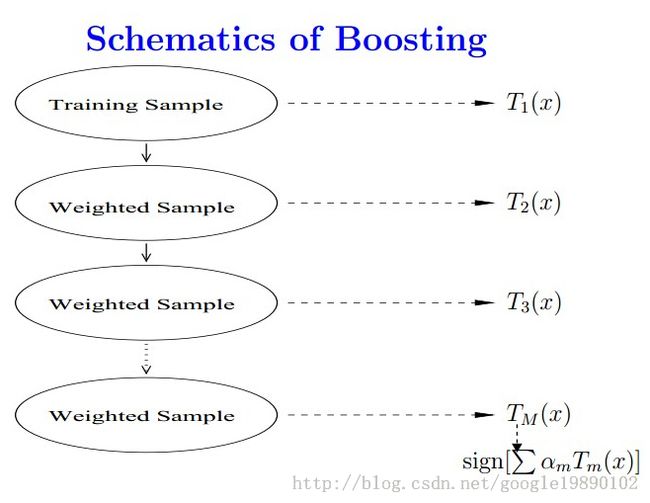
在
Boosting
算法中,初始化时对每个训练样本赋予相等的权重,如
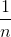 ,然后用该学习算法对训练集训练
,然后用该学习算法对训练集训练
 轮,每次训练后,对训练失败的训练样本赋予更大的权重,也就是让学习算法在后续的学习中几种对比较难学的训练样本进行学习,从而得到一个预测函数序列
轮,每次训练后,对训练失败的训练样本赋予更大的权重,也就是让学习算法在后续的学习中几种对比较难学的训练样本进行学习,从而得到一个预测函数序列
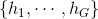 ,其中每个
,其中每个
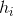 都有一个权重,预测效果好的预测函数的权重较大。最终的预测函数为对于分类和回归问题可采用如下的两种方法:
都有一个权重,预测效果好的预测函数的权重较大。最终的预测函数为对于分类和回归问题可采用如下的两种方法:
(图片来自参考文章2)
AdaBoost
和
GBDT(Gradient Boosting Decision Tree)
是基于
Boosting
思想的两个最著名的算法。
参考文章
1、《统计学习方法》
2、统计学习方法——CART, Bagging, Random Forest, Boosting