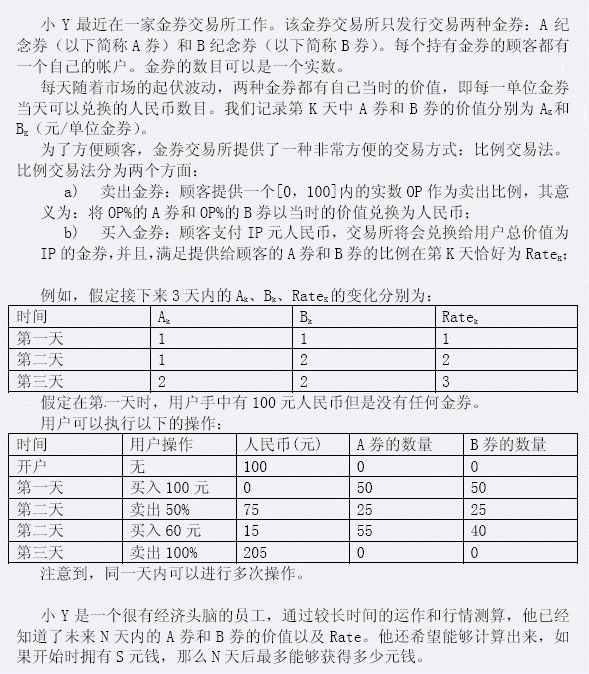
BZOJ 1492 货币兑换 Cash 平衡树维护凸包 CDQ分治

题目大意：

这题真是为难了我1B。。。做了三天，两种方法都试过了一遍，真是膜拜NOI的神犇们能在一个多小时内干掉这道题

首先我们分析一下操作 首先是卖出

假设我们手中有一堆A券和一堆B券 选择在一些天数分天卖出

那么这些天中一定有一天，卖出同样比例的证券可以获得的钱最多

我们选择这一天全部卖出 一定比分天卖出更优

然后是买入 由于卖出是一天 对于任意一天卖出 我分开买 那么一定有一天花同样的钱买入证券后在那一天卖出获利最大

选择在那一天全部买入 一定比分天买入更优

故买入和卖出都是在一天完成，而且都是倾巢买入/卖出

然后。。这题一看就是斜率优化 连递推式都是P=A[i]*X[i]+B[i]*Y[i] 万事俱备 就是AB不单调！

斜率不单调其实也好办 反正是凸包 平衡树维护不就简单了

简单个熊啊！！！

第一天下午开始写，第二天早上还在调，下午才AC，写了足足5.5KB。。

SPLAY各种挂 调的我都快被SPLAY了

此外这题递推式不满足队列优化的条件、、只能在平衡树上找斜率，着实坑了我1B。。。

然后是代码 边界讨论那里写的有点累赘 见谅了

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define M 100100
#define null (&empty)
using namespace std;
typedef pair<double,double> point;
struct List{
    point p;
    double slope;
    List *last,*next;
}head;
typedef pair<int,List*> P;
struct abcd{
    point num;
    List *pos;
    int size;
    abcd*ls,*rs;
    void sizmaintain(){
        size=1;
        if(ls)size+=ls->size;
        if(rs)size+=rs->size;
    }
}empty,*root=null,*Tar;
void zig(abcd*&x)
{
    abcd*k=x->ls;
    x->ls=k->rs;
    k->rs=x;
    x=k;
    x->rs->sizmaintain();
    x->sizmaintain();
}
void zag(abcd*&x)
{
    abcd*k=x->rs;
    x->rs=k->ls;
    k->ls=x;
    x=k;
    x->ls->sizmaintain();
    x->sizmaintain();
}
void splay(abcd *&x,abcd **y)
{
    if(x==Tar)return ;
    if(x==*y)
    {
        if(x->ls==Tar){  zig(x); return ;  }
        else if(x->rs==Tar){  zag(x); return ;  }
    }
    if(x->ls->ls==Tar) zig(x),zig(x);
    else if(x->rs->rs==Tar) zag(x),zag(x);
    else if(x->ls->rs==Tar) zag(x->ls),zig(x);
    else if(x->rs->ls==Tar) zig(x->rs),zag(x);
}
void insert(abcd*&x,point y,List *z)
{
    Tar=x;
    if(x==null){
        Tar=x=new abcd;
        x->num=y;
        x->pos=z;
        x->size=1;
        x->ls=x->rs=null;
        return ;
    }
    x->size++;
    if(y<x->num)insert(x->ls,y,z);
    else insert(x->rs,y,z);
    splay(x,&root);
}
void update(abcd*&x,point y,abcd**z)
{
    int re=x->ls->size;
    if(y==x->num)
    {
        Tar=x;
        return ;
    }
    if(y<x->num) update(x->ls,y,z);
    else update(x->rs,y,z);
    splay(x,z);
}
List* pre(abcd*x,point y)
{
    if(x==null)return &head;
    if(y<=x->num)return pre(x->ls,y);
    List*z=pre(x->rs,y);
    if(z->p<x->num)    return x->pos;
    return z;
}
double getslope(point p1,point p2)
{
    if(p1.first==p2.first)
        return 2147483647*(p2.second>p1.second?1:-1);
    return (double)( p2.second-p1.second )/( p2.first-p1.first );
}
void insert_point(point p)
{
    if(!head.next)
    {
        List*temp=new List;
        head.next=temp;
        temp->p=p;
        temp->next=NULL;
        temp->last=&head;
        temp->slope=2147483647;
        insert(root,p,temp);
        return ;
    }
    List*pos=pre(root,p);
    if( pos->next && pos->next->p == p )
        return;
    if(pos==&head)
    {
        pos=head.next;
        while(1)
        {
            pos->slope = getslope( p , pos->p );
            if(!pos->next)
                break;
            if( pos->next->slope > pos->slope )
                pos=pos->next;
            else
                break;
        }
         
        List*temp=new List;
        temp->next=pos;
        pos->last=temp;
        head.next=temp;
        temp->last=&head;
        temp->p=p;
        temp->slope=2147483647;
        update(root,temp->next->p,&root);
        root->ls=null;
        root->sizmaintain();
        insert(root,p,temp);
        return ;
    }
    if(!pos->next)
    {
        List*temp=new List;
        while(1)
        {
            temp->slope = getslope( pos->p , p );
            if(pos->last==&head)
                break;
            if( temp->slope > pos->slope )
                pos=pos->last;
            else
                break;
        }
        pos->next=temp;
        temp->last=pos;
        temp->p=p;
        temp->next=NULL;
        update(root,pos->p,&root);
        root->rs=null;
        root->sizmaintain();
        insert(root,p,temp);
        return ;
    }
    List*pos2 = pos->next;
    if( getslope(pos->p,p) < getslope(p,pos2->p) )
        return ;
    List*temp = new List;
    while(1)
    {
        pos2->slope=getslope(p,pos2->p);
        if(!pos2->next)
            break;
        if( pos2->next->slope > pos2->slope )
            pos2=pos2->next;
        else
            break;
    }
    while(1)
    {
        temp->slope = getslope( pos->p , p );
        if(pos->last==&head)
            break;
        if( temp->slope > pos->slope )
            pos=pos->last;
        else
            break;
    }
    temp->p=p;
    temp->next=pos2;
    pos2->last=temp;
    temp->last=pos;
    pos->next=temp;
    update(root,pos->p,&root);
    update(root,pos2->p,&(root->rs) );
    root->rs->ls=null;
    root->rs->sizmaintain();
    root->sizmaintain();
    insert(root,p,temp);
}
List* getans(abcd *x,double y)//找到第一个斜率大于y的点
{
    head.next->slope=2147483647;
    if(x==null)return head.next;
    double s = x->pos->slope;
    if(y>=s)return getans(x->ls,y);
    List*z=getans(x->rs,y);
    if(z->slope>s)return x->pos;
    return z;
}
/*
List* pre(abcd*x,point y)
{
    if(x==null)return &head;
    if(y<=x->num)return pre(x->ls,y);
    List*z=pre(x->rs,y);
    if(z->p<x->num)    return x->pos;
    return z;
}
*/
double A[M],B[M],Rate[M],X[M],Y[M],f;
int n;
int main()
{
    int i;
     
    //freopen("cash.in","r",stdin);
    //freopen("cash.out","w",stdout);
     
    empty.ls=empty.rs=null;
    cin>>n>>f;
    for(i=1;i<=n;i++)
        scanf("%lf%lf%lf",&A[i],&B[i],&Rate[i]);
    for(i=1;i<=n;i++)
    {
        if(i!=1)
        {
            point p=getans( root , - A[i] / B[i] )->p;
            f=max( f , A[i] * p.first + B[i] * p.second );
        }
        X[i] = f / ( A[i] + B[i] / Rate[i] );
        Y[i] = f / ( A[i] * Rate[i] + B[i] );
        insert_point( make_pair( X[i] , Y[i] ) );
        //printf("%d %.3lf %.3lf %.3lf\n",i,f,X[i],Y[i]);
    }
    printf("%.3lf\n",f);
}

第二种方法就简单多了 CDQ分治

CDQ分治的思想是f[i]的决策点一定在0~i-1之中，于是我们分治，其中对于每一层递归[l,r]，二分出一个中点mid

然后递归求出[l,mid]中所有的f值，对[l,mid]中的点建立凸包，用[mid+1,r]中的所有元素的斜率去询问，得到[l,mid]中所有的点对[mid+1,r]中所有点的影响

然后递归求出[mid+1,r]中的所有f值

其中当我们递归到任意[i,i]时，0~i-1中所有点对这个点的影响都已经计算过，于是直接得出f[i]即可

这个算法不难理解，但是我挂了半天。。CDQ没写错，sort居然写错了，按照Rate排了个序，眼科大夫死得早啊

最可怕的是前四个点居然还过了 这是要有多水的节奏

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define M 100100
using namespace std;
typedef pair<double,double> P;
int n,stack[M],top;
double f[M];
struct abcd{
    double A,B,Rate;
    double slope;
    int pos;
}q[M],nq[M];
bool operator < (abcd x,abcd y)
{
    return x.slope < y.slope;
}
P p[M],np[M];
double getslope(P x,P y)
{
    if(x.first==y.first)
        return 2147483647*(y.second>=x.second?1:-1);
    return (y.second-x.second)/(y.first-x.first);
}
void CDQ(int l,int r)
{
    int i,mid=l+r>>1;
    if(l==r)
    {
        f[mid]=max( f[mid] , f[mid-1] );
        p[mid].first = f[mid] / ( q[mid].A + q[mid].B / q[mid].Rate ) ;
        p[mid].second = f[mid] / ( q[mid].A * q[mid].Rate + q[mid].B ) ;
        return ;
    }
    int l1=l,l2=mid+1;
    for(i=l;i<=r;i++)
        if(q[i].pos<=mid)
            nq[l1++]=q[i];
        else
            nq[l2++]=q[i];
    memcpy( q+l , nq+l , sizeof(q[0])*(r-l+1) );
    CDQ(l,mid);
    top=0;
    for(i=l;i<=mid;i++)
    {
        while(top>1)
            if( getslope(p[stack[top-1]],p[stack[top]]) < getslope(p[stack[top]],p[i]) )
                stack[top--]=0;
            else
                break;
        stack[++top]=i;
    }
    for(i=mid+1;i<=r;i++)
    {
        while(top>1)
            if( getslope(p[stack[top-1]],p[stack[top]]) < q[i].slope )
                stack[top--]=0;
            else
                break;
        f[q[i].pos]=max(f[q[i].pos],q[i].A*p[stack[top]].first+q[i].B*p[stack[top]].second);
    }
    CDQ(mid+1,r);
    l1=l;l2=mid+1;
    for(i=l;i<=r;i++)
        if ( ( p[l1]<p[l2] || l2>r ) && l1<=mid )
            np[i]=p[l1++];
        else np[i]=p[l2++];
    memcpy( p+l , np+l , sizeof(p[0])*(r-l+1) );
}
int main()
{
    int i;
     
    //freopen("cash.in","r",stdin);
    //freopen("cash.out","w",stdout);
     
    cin>>n>>f[0];
    for(i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf",&q[i].A,&q[i].B,&q[i].Rate);
        q[i].slope=-q[i].A/q[i].B;
        q[i].pos=i;
    }
    sort(q+1,q+n+1);
    CDQ(1,n);
    printf("%.3lf\n",f[n]);
}

最后还是来一句膜拜神犇吧 07年的第一题就这么难 这么难 这么难0.0.0.0.0.0.0.0.0.0