数理统计中的点估计

• 统计推断的基本问题有二：估计问题，和假设检验问题.
• 本章讨论总体参数的点估计和区间估计.理解这两种估计的思想，掌握求参数估计量的方法和评判估计量好坏的标准.

点估计

问题的提出

设灯泡寿命 T～N(μ,σ2) ，但参数 μ 和 σ2 未知. 现在要求通过对总体抽样得到的样本，构造两样本函数分别 μ 和 σ2 作出估计,称为估计量, 记为 μ′ 和 σ2′ ,代入观察值 x=(x1,…,xn) ，得相应估计值.在不致混淆时统称为估计.
借助于总体的一个样本，构造适当的样本函数来估计总体 S 未知参数的值的问题称为参数的点估计问题.
• 两种常用的构造估计量的方法: 矩估计法和极大似然估计法.

矩估计

思想与方法

设总体k阶矩存在，
对于连续型总体X，它的m阶原点矩为

μk:=E(Xk)=∫+∞−∞xkdF(x,θ)

若X为离散型的，则

μk:=E(Xk)=∑i=1nxkF(x,θ)

这里 θ 为未知参数向量. 可见 μk 是 θ 的函数，改记为 μk(θ) .

设测得10个灯泡寿命(失效时间)分别为

166，185，232，242，264，268，270，275，285，312

(小时）.
那么自然想到平均寿命为

(166+185+...+312)/10=249.9（小时）

即用样本均值的观测值 x¯ 来估计总体的平均寿命(期望寿命) μ
即

μ^=X¯¯¯=1n(X1+X2+⋯+Xn)

对 μk(θ) ,k阶样本原点矩为

μk^(θ)=Mk=1n(Xk1+Xk2+⋯+Xkn)

这就是矩估计的思想：
用样本的k阶矩作为总体k阶矩的估计量.如果未知参数有m个，则可建立m个方程

μ^k(θ1,…,θm)=Mk,k=1,…,m

(如总体 μm 存在). 从中解出 θj=θj(X1,X2,…,Xn) , 改记为 θ^ ,并作为 θj 的估计量. 称这种估计量为 矩估计量, 相应观察值称为 矩估计值.
由上一篇文章讲得经验df函数性质可以知道
样本矩几乎处处收敛于总体矩，

• 样本矩的连续函数也几乎处处收敛于总体矩的相应的连续函数,它保证:几乎每次从容量足够大的样本观测值，都可得到相应总体参数的近似值.

例题1

设总体 X 的二阶矩存在，求总体 X 的期望和方差的矩估计量.
解：
m=2 ，可得

（将 μ^和σ^2 当做未知量，将 Xi 当做已知量，解方程组）
解得

结论：不论总体有什麽样的分布，只要它的 期望和 方差存在，则它们的矩估计量都分别是其样本均值和样本的二阶中心矩.
为突出是矩估计量，也常加下标M，例如 μ^M

例题2

设总体 X～U(0,θ) , θ 未知， (X1,…,Xn) 是一个样本, 试求 θ 的矩估计量.
解:
直接由上例结果，令解得 θ 的矩估计量

θ^M=2X¯¯¯

例题3

设总体 ，即 具有概率密度

这里a，b为未知参数， (X1,X2,…,Xn) 为抽自X的简单随机样本
由于 E(X)=a+b2, D(X)=(b−a)212
令

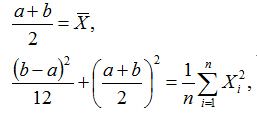
由此可解得a和b的矩估计为

a^=X¯¯¯−3√Snb^=X¯¯¯+3√Sn

其中 S2n=1n∑ni=1(Xi−X¯¯¯)2

极大似然估计法

思想和方法

假设在一个罐中放着许多黑球和白球，并假定已知它们的数目之比为 ，但不知哪种颜色的球多。如果我们有放回地从罐中抽取 个球，则其中的黑球数 服从二项分布：

P(X=k)=Ck3pkq3−k,k=0,1,2,3

其中 p=罐中黑球数目罐中全部球的数目,q=1−p ，由假设知道 p 可能取值为 14或34 .
现在根据样本中的黑球数，来估计未知参数 ，也就是说在 14和34 之间作一选择。对抽样的四种可能结果计算出相应的概率：

从表1中可见，如果样本中的黑球数为0，那么具有X=0的样本来自 p=14 的总体的可能性比来自 p=34 的总体的可能性大，这时应当估计p为 14 而不是 34 。如果样本中黑球数为2，那么具有X=2的样本来自 p=34 的总体的可能性比来自 p=14 的总体的可能性大，这时应当估计p为 34 而不是 14 。从而可以选择估计量：

也就是说根据样本的具体情况来选择估计量 p^ ，使得出现该样本的可能性最大。
一般地，若总体X具有概率密度 p(x,θ1,θ2,…,θk) ，其中 θ1,θ2,…,θk 为未知参数，又设 (x1,x2,…,xn) 是样本的一组观察值，那么样本 (X1,X2,…,Xn) 落在点 (x1,x2,…,xn) 的邻域内的概率为 ∏ni=1p(xi;θ1,θ2,…,θk)dxi ，它是 θ1,θ2,…,θk 的函数。
最大似然估计的直观想法是：既然在一次试验中得到了观察值 (x1,x2,…,xn) ，那么我们认为样本落入该观察值 (x1,x2,…,xn) 的邻域内这一事件应具有最大的可能性，所以应选取使这一概率达到最大的参数值作为参数真值的估计。记
离散型时θ应使

L(x,θ):=L(x1,…,xn;θ)=∏i=1np(xi;θ)

最大;
连续型时θ应使

f(x1,…,xn;θ)dx1…dxn=∏i=1nf(xi;θ)dxi

也即, 使 L(x,θ)=∏ni=1f(xi;θ) 最大.
称 L(x,θ) 为样本的 似然函数.

这样得到的估计值, 称为参数θ的极大似然估计值, 而相应的统计量称为参数θ的极大似然估计量.
求 θ 的最大似然估计就是求似然函数 L(x;θ) 的最大值点的问题。
如 L(x;θ) 关于 θ 可微, 这时也可以从方程

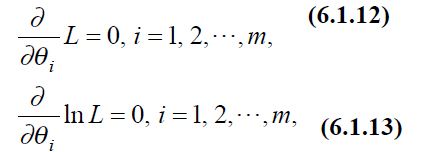
解出. (1.12)和(1.13)都称为 似然方程.
由于在许多情况下，求 lnL(x;θ) 的最大值点比较简单，而且 lnx 是 x 的严格增函数，因此在 lnL(x;θ) 对 θi（i=1,2,…,k） 的偏导数存在的情况下， 可由(1.13)式求得.
解这一方程组，若 lnL(x;θ) 的驻点唯一，又能验证它是一个极大值点，则它必是 lnL(x;θ) 的最大值点，即为所求的最大似然估计。但若驻点不唯一，则需进一步判断哪一个为最大值点。还需指出的是，若 lnL(x;θ) 对 θi（i=1,2,…,k） 的偏导数不存在，则我们无法得到方程组（1.13），这时必须根据最大似然估计的定义直接求 L(x,θ) 的最大值点。
有时我们需要估计 g(θ1,θ2,…,θk) ，如果 θ^1,θ^2,…,θ^k 分别是 θ1,θ2,…,θk 的最大似然估计，且 g(θ1,θ2,…,θk) 为连续函数，则 g(θ^1,θ^2,…,θ^k) 是 g(θ1,θ2,…,θk) 的最大似然估计。

例题1

设 X～N(μ,σ2) ， x1,…,xn 为一个样本值求未知参数 μ 和 σ2 的极大似然估计量.
解：
似然函数为

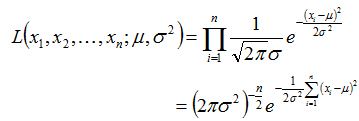
它的对数为

解对数似然方程组（见1.13）：

可得

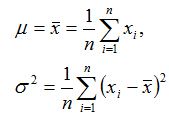
由于对数似然方程组有唯一解，且它一定是最大值点，于是 μ 和 σ2 的最大似然估计为

例题2

求事件发生的概率 的最大似然估计。
解：
若事件A发生的概率 P(A)=p ，定义随机变量

则 X～B(1,p) ，其概率分布为

P(X=xi)=pxi(1−p)1−xi,xi=0,1

设 (X1,X2,…,Xn) 为抽自X的样本，则似然函数为

由对数似然方程

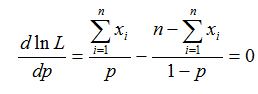
解得

注意到 ∑ni=1xi≤n ，容易验证 d2lnLdp2 在 x¯ 处取得负值，于是 x¯ 是 lnL 的最大值点，因而p的最大似然估计为 p^=X¯¯¯
于是我们有结论：频率是概率的最大似然估计。

例题3

设总体 X～U[a,b] ， (X1,X2,…,Xn) 为抽自X的样本，求未知参数a,b的最大似然估计。
解：
由于X的密度函数为

因此似然函数为

显然，作为a,b的二元函数，L是不连续的。这时我们不能用方程组（1.13）来求最大似然估计，而必须从最大似然估计的定义出发来求L的最大值点。
为使L达到最大，b-a应尽量地小，但b又不能小于 max{x1,x2,…,x3} ，否则 L(x1,x2,…,x3;a,b)=0 ；类似地，a 又不能大于 min{x1,x2,…,x3} 。因此a,b的最大似然估计为

估计的优良性准则

同一个未知参数，可以有几种不同的估计，这时就存在采用哪一种估计的问题。另一方面，对同一个参数，用矩估计法和最大似然估计法，即使得到同一个估计，也存在衡量该估计量优劣的问题。设 θ 为未知参数， θ^ 是 θ 的估计，直观上讲， θ^ 与 θ 越接近越好，为了度量 θ^ 与 θ 的接近程度，我们可以采用 |θ^−θ| 作为衡量的标准，但由于 θ^(X1,X2,…,Xn) 依赖于样本，它本身是随机变量，而 θ 又是未知的，因此很难采用。下面我们从不同的角度，提出几种衡量估计优劣的标准。

一致性

定义1：

设 θ^(X1,X2,…,Xn) 是总体X分布的未知参数 θ 的估计量，若 θ^ 依概率收敛于 θ ，即对任意的 ε>0 ，

limn→∞P(|θ^−θ|<ε)=1

则称 θ^ 是 θ 的一致估计。
满足一致性的估计量 θ^ ，当样本容量n 不断增大时， θ^ 观察值能越来越接近参数真值 。这很容易理解，当样本容量n越大时，信息越多，当然估计就越准确。
由大数定律知，样本均值 X¯¯¯ 是总体均值 μ （即 E(X) ）的一致估计。还有，样本修正方差 S2 是总体方差 σ2 （即 D(X) ）的一致估计。

例题1

若总体X服从正态分布 N(μ,σ2) ， (X1,X2,…,Xn) 是来自总体 X的容量为n的样本， EXi=μ ， DXi=σ2 ， i=1,2,…,n ，则由大数定律知， X¯¯¯ 依概率收敛于 μ ，即

limn→∞P(|X¯¯¯−μ|<ε)=1

也即未知参数 μ 的最大似然估计或矩估计 μ^=X¯¯¯ 是 μ 的一致估计。

例题2

若总体X服从泊松分布 P(λ) ， (X1,X2,…,Xn) 是从总体 X 中抽取的容量为 n 的样本，且 EXi=λ ， DXi=λ ， i=1,2,…,n ，则 X¯¯¯ 依概率收敛于 λ ，故未知参数 λ 的最大似然估计或矩估计 λ^=X¯¯¯ 是 λ 的一致估计。

例题3

若总体 X 服从0-1分布， P(X=1)=p,0<p<1 ， (X1,X2,…,Xn) 是从 X 中抽取的容量为 n 的样本 EXi=p ， DXi=p(1−p) ， i=1,2,…,n 则 X¯¯¯ 依概率收敛于 p ，故未知参数 p 的最大似然估计或矩估计 p^=X¯¯¯ 是 p 的一致估计。

无偏性

设 θ 为总体分布的未知参数， θ^(X1,X2,…,Xn) 是 θ 的一个估计，它是一个统计量。对于不同的样本 (X1,X2,…,Xn) ， θ^(X1,X2,…,Xn) 取不同的值。

定义2

如果 θ^(X1,X2,…,Xn) 的均值等于未知参数 θ ，即 E[θ^(X1,X2,…,Xn)]=θ 对一切可能的 θ 成立 ————（3）
则称 θ^(X1,X2,…,Xn) 为 θ 的无偏估计 。
无偏估计的意义是：用 θ^(X1,X2,…,Xn) 去估计未知参数 θ ，有时候可能偏高，有时候可能偏低，但是平均说来等于未知参数 θ 。
在（3）式中，对一切可能的 θ ，是指在每个具体的参数估计问题中，参数 θ 取值范围内的一切可能的值。例如，若 θ 是正态总体 N(μ,σ2) 的均值 μ ，那么它的一切可能取值范围是 (−∞,+∞) 。若 θ 是方差 σ2 ，则它的取值范围为 (0,+∞) 。我们之所以要求（3）对一切可能的 θ 都成立，是因为在参数估计中，我们并不知道参数的真值。因此，当我们要求一个估计量具有无偏性时，自然要求它在参数的一切可能取值范围内处处都是无偏的。

例题1

设 (X1,X2,…,Xn) 是抽自均值为 μ 的总体的样本，考虑 μ 的如下估计量：

μ^1=X1μ^2=X1+X22μ^3=X1+X2+Xn−1+Xn4

假设 n≥4
因为 EXi=μ ，容易验证 Eμ^i=μ,i=1,2,3 ，所以 μ 都是 的的无偏估计，但是

μ^4=2X1μ^5=X1+X23

都不是 μ 的的无偏估计。
对于任一总体 X ，由于 EX¯¯¯=μ ，所以 X¯¯¯ 是 μ 的的无偏估计，但由于 ES2n=E[1n∑ni=1(Xi−X¯¯¯)2]=n−1nσ2 ，故 S2n 不是总体方差 σ2 的无偏估计，而修正的样本方差 是总体方差 S2n=1n−1∑ni=1(Xi−X¯¯¯)2 的无偏估计。
若 θ^ 是 θ 的估计， g(θ) 为 θ 的实函数，通常我们总是用 g(θ^) 去估计 g(θ) ，但是值得注意的是，即使 Eθ^=θ ，也不一定有 E(g(θ^))=g(θ) 。

例题2

修正样本方差的标准差 S 不是总体标准差 σ 的无偏估计。
事实上，由于 σ2=E(S2)=DS2+[ES]2≥[ES]2 ，从而 σ≥ES ，即 S 不是 σ 的无偏估计。
若 θ 的估计 θ^ 不是无偏的，但当 n→∞ 时， Eθ^→θ ，则称 θ^ 是 θ 的渐近无偏估计。显然，样本方差 S2n 是总体方差的一个渐近无偏估计。
无偏性对估计量而言是很基本的要求，它的直观意义是没有系统误差。由上例知，对于一个未知参数，它的无偏估计可以不止一个。那么，怎么来比较它们的好坏呢？我们很自然地想到，一个好的估计量应该方差比较小，只有这样才能得到比较稳定的估计值。

有效性

定义3

设 θ^1(X1,X2,…,Xn) 和 θ^2(X1,X2,…,Xn) 均为参数 θ 的无偏估计，如果

Dθ^1<Dθ^2

则称 θ^1 较 θ^2 有效。当 θ^(X1,X2,…,Xn) 是所有无偏估计中方差最小时，称 θ^(X1,X2,…,Xn)
为 最小方差无偏估计。

例题

设 (X1,X2,…,Xn) 是来自总体 X 的容量为 n 的样本，证明总体均值 μ （即 EX ）的估计量 μ^1=X¯¯¯ 比 μ^2=∑ni=1aiXi 有效，其中 ai≥0,i=1,2,…,n 且 ∑ni=1ai=1 。
证明
由于 Eμ^1=μ ， Eμ^2=E(∑ni=1aiXi)=μ∑ni=1ai=μ ，所以 μ^1,μ^2 均是 μ 的无偏估计。
又

从而

所以 X¯¯¯ 比 ∑ni=1aiXi 有效。
由上例和一致性知，样本均值 X¯¯¯ 是总体均值 μ （即 EX ）的一致最小方差无偏估计。同样还可以证明，样本修正方差 S2 是总体方差 σ2 （即 DX ）的一致最小方差无偏估计。