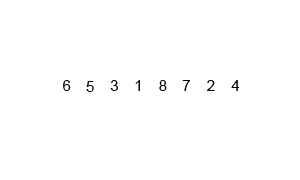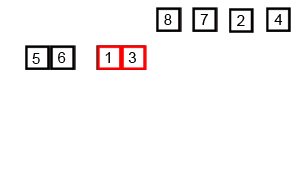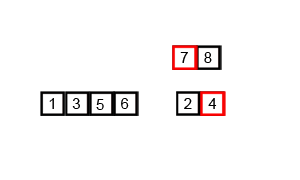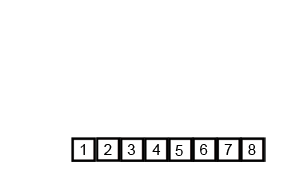离职总是很麻烦,老板人不错,得好好把工作对接完咯。晚上闲一下就写写博客。
前言
下面会讲到一些简单的排序算法(均基于java实现),并给出实现和效率分析。
使用的基类如下:
注意:抽象函数应为public的,我就不改代码了
public abstract class Sortable {
protected String LABLE="排序算法";
//比较两个数(使用了Integer中sort的源码)
protected int compare(int x, int y) {
return (x < y) ? -1 : ((x == y) ? 0 : 1);
}
//同上,不过返回改为bool
protected boolean less(int x,int y){
return compare(x,y) <0;
}
//交换数组中的两个值
protected void exch(int[] a,int i,int j){
Integer temp = a[i];
a[i] = a[j];
a[j] = temp;
}
//子类需要实现的排序算法
public abstract void sort(int[] a);
public String getLABLE() {
return LABLE;
}
}
冒泡排序
最常见的,毕竟老师教给我们的的第一种排序算法。实现起来很简单,不过实际应用很少(正常情况下),复杂度O(n²)。
原理
趟一趟的比,每一趟中,循环剩余的数,和后一个进行比较,若比它小则交换。这样一趟下来最小的在第一个,最大的在最后一个。总共比n-1趟。
实现
import com.anxpp.sort.base.Sortable;
/**
* 最简单的冒泡排序
*
* @author anxpp.com
* 原理:比较相邻两个元素,从第一对开始比较一直到最后一对,若顺序不对就交换(感觉就像冒泡一样)。
* 一趟比较后,最大(或最小)的会位于最后的位置,然后再以类似方式比较前面的元素。
*/
public class BubbleSort extends Sortable {
public BubbleSort(){
super.LABLE = "冒泡排序";
}
@Override
public void sort(int[] a) {
for(int i=0;i<a.length-1;i++){
for(int j=0;j<a.length-1-i;j++){
if(less(a[j+1],a[j])){
exch(a,j,j+1);
}
}
}
}
}
优化
上面的算法,无论的你的数据怎么样,始终都要比n²次,效率很低。若你的数据局部有序,经过几趟交换以后,已经有序,则不用继续往下比。效率会高很多(绝大多数情况下)。优化代码如下:
import com.anxpp.sort.base.Sortable;
/**
* 设置标志优化后的冒泡排序
* @author anxpp.com
*
* 原理:比较相邻两个元素,从第一对开始比较一直到最后一对,若顺序不对就交换(感觉就像冒泡一样)。
* 一趟比较后,最大(或最小)的会位于最后的位置,然后再以类似方式比较前面的元素。
* 优化:传统的冒泡排序,总是要比较那么多次,如果在某趟完成后,并无交换表示数据已经有序,所以设置
* 一个标志,如某趟比较完成后没有发生,则不再继续后面的运算直接返回即可,其实,有时候效率反而会比传统的低!
* 其他:据说分而治之也能有用到冒泡,这里就不深究了...
*/
public class BetterBubbleSort extends Sortable {
public BetterBubbleSort(){
super.LABLE = "冒泡排序优化";
}
@Override
public void sort(int[] a) {
boolean didSwap;
for(int i=0;i<a.length-1;i++){
didSwap = false;
for(int j=0;j<a.length-1-i;j++){
if(less(a[j+1],a[j])){
exch(a,j,j+1);
didSwap = true;
}
}
if(!didSwap) return ;
}
}
}
选择排序
和冒泡复杂度一样O(n²),但是时间上可能会比冒泡稍微快一点,因为交换的次数比冒泡少。
原理
选择排序可以说是最好理解的算法。就是每次遍历一趟,找出最小的数,放到最前端。(这里说的是最前,是指无序的队列中的最前)
实现
import com.anxpp.sort.base.Sortable;
/**
* 选择排序
* @author anxpp.com
*
*/
public class SelectionSort extends Sortable {
public SelectionSort(){
super.LABLE = "选择排序";
}
@Override
public void sort(int[] a) {
for(int i=0;i<a.length;i++){
int min=i;
for(int j=i+1;j<a.length;j++){
if(less(a[j],a[min])){
min = j;
}
}
exch(a,i,min);
}
}
}
插入排序
时间复杂度O(n²)。
原理
遍历未排序序列。把未排序数列的第一个数和已排序数列的每一个数比较,若比它大则交换。经典的理解方式就是理解成摸牌时候理牌的顺序。我上面的实现是直接交互数字,若是把大的数直接往后移效率还会更高。
实现
import com.anxpp.sort.base.Sortable;
/**
* 插入排序
* @author anxpp
*
*/
public class InsertionSort extends Sortable {
public InsertionSort(){
super.LABLE = "插入排序";
}
@Override
public void sort(int[] a) {
for(int i=1;i<a.length;i++){
for(int j=i;j>0;j--){
if(less(a[j],a[j-1])){
exch(a,j,j-1);
}
else break;
}
}
}
}
适合插入排序的数据
当你的数据是基本有序的时候且数据量小,利用插入排序的时候,效率会很高。若数据为逆序的话,效率很低。
希尔排序
可以看出是插入排序的一种优化,或者是预处理。希尔排序就是先进行h-sort,也就是让间隔为h的元素都是有序的。普通的插入排序就是1-sort。
原理
主要就是选定一个h的有序数组来进行预排序。这样最后进行插入排序的时候,能使数据局部有序。就算交换的话,交换的次数也不会很多。这样h序列称为递增序列。希尔的性能很大部分取决于递增序列.一般来说我们使用这个序列3x + 1.

实现
import com.anxpp.sort.base.Sortable;
/**
* 希尔排序
* @author anxpp.com
*
*/
public class ShellSort extends Sortable {
public ShellSort(){
super.LABLE = "希尔排序";
}
@Override
public void sort(int[] a) {
int h=1;
while(h<a.length/3){
h=3*h+1;
}
while(h>=1){
for(int i=h;i<a.length;i++){
for(int j=i;j>=h;j=j-h){
if(less(a[j],a[j-h])){
exch(a,j,j-h);
}
else break;
}
}
h=h/3;
}
}
}
性能
对于希尔排序的性能其实无法准确表示。介于O(nlogn)和O(n²)之间,大概在n的1.5次幂左右。
希尔排序对于中大型数据的排序效率是很高的,而且占用空间少,代码量短。而且就算是很大的数据,用类似快排这种高性能的排序方法,也仅仅只比希尔快两倍或者不到。
归并排序
复杂度O(nlogn).
核心思想就是采用分而治之的方法,递归的合并两个有序的数组。效率比较高,缺点是空间复杂度高,会用到额外的数组。
原理
核心代码是合并的函数。合并的前提是保证左右两边的数组分别有序,在合并之前和之后在Java中我们可以用断言来保证数组有序。合并的原理其实也很简单,先把a数组中的内容复制到额外储存的temp数组中去。分别用两个index指向a数组的起始位置和中间位置,保证a数组左右两边有序,比如i,j。现在开始从头扫描比较左右两个数组,若a[i]<=a[j],则把a[i]放到temp数组中去,且i向前走一步。反正则放a[j],且j走一步。若其中一个数组走完了,则把另一个数组剩余的数直接放到temp数组中。我们用递归的方式来实现左右两边有序。递归到数组只有1个数时肯定是有序的,再合并2个数,再退出来合并4个数,以此类推。
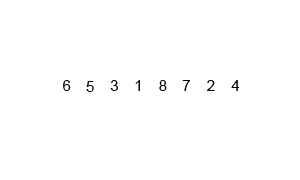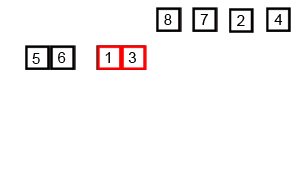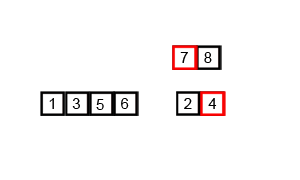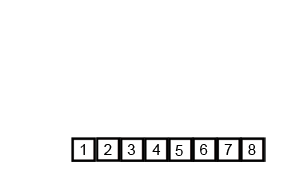
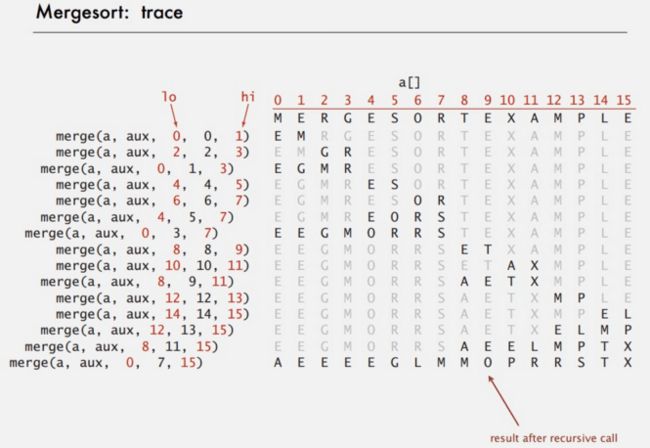
实现
import com.anxpp.sort.base.Sortable;
/**
* 归并排序
* @author anxpp.com
*
*/
public class MergeSort extends Sortable {
public MergeSort(){
super.LABLE = "归并排序";
}
int[] temp ;
private void merge(int[] a, int l, int m, int h){
for(int i=l;i<=h;i++){
temp[i]=a[i];
}
int i=l;
int j=m+1;
for(int k=l;k<=h;k++){
if(i>m) a[k]=temp[j++];
else if(j>h) a[k]=temp[i++];
else if(less(temp[i],temp[j])) a[k]=temp[i++];
else a[k] = temp[j++];
}
}
private void sort(int[] a,int l,int h) {
if(l<h){
int mid = (l+h)/2;
sort(a,l,mid);
sort(a,mid+1,h);
if (!less(a[mid+1], a[mid])) return;
merge(a,l,mid,h);
}
}
@Override
public void sort(int[] a) {
temp = new int[a.length];
sort(a,0,a.length-1);
}
}
优化
归并排序对小数组排序时,由于会有多重的递归调用,所以速度没有插入排序快。可以在递归调用到小数组时改采用插入排序。小数组的意思是差不多10个数左右。
如果递归时判断已经有序则不用继续递归。也可以增加效率。
private void sort(int[] a,int l,int h) {
if(l<h){
int mid = (l+h)/2;
sort(a,l,mid);
sort(a,mid+1,h);
if (!less(a[mid+1], a[mid])) return;
merge(a,l,mid,h);
}
}
另外在合并时交互两个数组的顺序,能节省复制数组到辅助数组的时间,但节省不了空间。

适用范围
如果你对空间要求不高,且想要一个稳定的算法。那么可以使用归并排序。
快速排序
传说中最快的排序算法,听说能裸写快排,月薪可上10k...
快排平均情况下时间复杂度O(nlogn),最糟糕情况O(n²)。O(n²)主要是因为选定的主元是极端值造成的,比如说最大值,最小值。不过这种情况一般很少出现,所以在进行快排之前我们需要对数组进行乱序,尽量避免这种情况的发生。
原理
第一步打乱数组。
然后也是分治法。归并是先分再合并。快排是先排序再分别排序两边。
排序过程核心思想是为了选出一个数,把数组分成左右两边,左边比主元小,右边比主元大。
选定第一个数作为主元。然后设定两个index指向数组首尾,比如i,j。接着从两边向中间扫描,分别用a[i]和a[j]和主元比较。若两边位置不对则交换a[i]和a[j],比如说a[i]在扫描过程中遇到a[i]>主元,那么则停止扫描,因为我们需要左边的数小于主元,反正右边也一样等到a[j]也停下来,则交换a[i]和a[j]。
得到中间的位置之后再分别左右递归排序。


实现
import com.anxpp.sort.base.Sortable;
/**
* 快速排序
* @author u
*
* 原理:选择一个基准元素,通过一趟扫描,将数据分成大于和不大于基准元素的两部分(分别在基准元素的两边),此时
* 基准元素就在未来排好后的正确位置,然后递归使用类似的方法处理这个基准元素两边的部分。
* 既然用了递归,难免在空间上的效率不高...
* 平均性能通常被认为是最好的
*/
public class quickSort extends Sortable {
public quickSort(){
super.LABLE = "快速排序";
}
/**
*
* @param a 要排序的列表
* @param low 左边位置
* @param high 右边位置
*/
private void sort(int[] a,int low,int high){
//左
int l =low;
//右
int h = high;
//基准值
int k = a[low];
//判断一趟是否完成
while(l<h){
//若顺序正确就比较下一个
while(l<h&&a[h]>=k)
h--;
if(l<h){
int temp = a[h];
a[h] = a[l];
a[l] = temp;
l++;
}
while(l<h&&a[l]<=k)
l++;
if(l<h){
int temp = a[h];
a[h] = a[l];
a[l] = temp;
h--;
}
}
if(l>low) sort(a,low,l-1);
if(h<high) sort(a,l+1,high);
}
@Override
public void sort(int[] a) {
sort(a,0,a.length-1);
}
}
优化
第一步的随机打乱数组,虽然会耗费一定时间,但却是必要的。同样的小数组的排序,快排不如插入排序。所以小数组可以直接采用插入排序。主元的选择方式可以有多种,比如随机选择主元。或者选取三个数,取中位数为主元,但是会耗费一定时间。
适用范围
虽然快速排序是不稳定的。但快速排序通常明显比其他Ο(nlogn)算法更快,因为它的内部循环很小。快速排序在对重复数据的排序时,会重复划分数据进行排序。虽然性能也还行,但这里可以进行改进,就是下面介绍的三向切分排序。
三向切分
快速排序的一种改进,使快排在有大量重复元素的数据,同样能保持高效。
原理
基本原理和快排差不多。三向切分的时候在划分数组时不是分为两组,而是分成三组。
实现
public class ThreeWaySort extends Sortable {
public void sort(int[] a,int l ,int h) {
if(l>=h) return;
int v = a[l];
int i=l;
int lv=l;
int gh=h;
while(i<=gh){
int cmpIndex = compare(a[i],v);
if(cmpIndex<0) exch(a,i++,lv++);
else if(cmpIndex>0) exch(a,i,gh--);
else i++;
}
sort(a,l,lv-1);
sort(a,gh+1,h);
}
@Override
void sort(int[] a) {
sort(a,0,a.length-1);
}
}
堆排序
时间复杂度O(nlogn),堆排序主要用二叉堆实现,在讲堆排序之前我们可以要先了解下二叉堆。
二叉堆
所谓的二叉堆用一颗二叉树表示,也就是每一个节点都大于它的左右子节点。也就是说根节点是最大的。
二叉树用数组存储,可以用下标来表示节点。比如i这个节点的父节点为i/2,左儿子为2*i,右儿子为2*i+1.
堆的操作主要有两种上浮和下沉。主要对应两种情况,比如在数组末尾添加节点,此时需要上浮节点,保证二叉堆的特点。反之在替换根节点是则需要下沉操作。
原理
分为两步。
- 把数组排成二叉堆的顺序
- 调换根节点和最后一个节点的位置,然后对根节点进行下沉操作。

实现
适用范围
堆排序也是不稳定的。
堆排序在空间和时间上都是O(nlogn),且没有最糟情况,但在平均情况下比快排慢。
所以现在大部分应用都是用的快排,因为它的平均效率很高,几乎不会有最糟情况发生。
但如果你的应用非常非常重视性能的保证,比如一些医学上的监控之类的。
那么可以使用堆排序。还有一个堆排序的缺点,是它无法利用缓存,几乎很少和相邻元素的比较。
运行时间比较
使用下面的代码测试以上排序算法:
import java.util.Random;
import com.anxpp.sort.base.Sortable;
/**
* 测试排序算法
* @author anxpp.com
*
*/
public class TestSort {
//需要排序的数字长度为LEN
private final static int LEN = 30000;
//最大值为MAX
private final static int MAX = 99999;
public static void main(String[] args){
//初始化排序算法
Sortable[] sortables = {
new BubbleSort(),new BetterBubbleSort(),new SelectionSort(),
new InsertionSort(),new ShellSort(),new MergeSort(),
new BetterMergeSort(),new quickSort(),new ThreeWayQuickSort()};
//产生源数据
Random random = new Random();
random.setSeed(System.currentTimeMillis());
int[][] a = new int[sortables.length][LEN];
int i = 0;
while(i++ < LEN-1){
int num = random.nextInt(MAX);
int j = 0;
while(j<sortables.length)
a[j++][i] = num;
}
//排序
for(i = 0;i<sortables.length;i++){
System.out.println(sortables[i].getLABLE()+":");
// print(a[i]);
// sortTime(a[i],sortables[i]);
System.out.println(sortTime(a[i],sortables[i]));
// print(a[i]);
}
}
public static int sortTime(int[] a,Sortable sortable){
long start = System.currentTimeMillis();
sortable.sort(a);
return (int) (System.currentTimeMillis()-start);
}
public static void print(int[] a){
for(int i = 0;i<a.length;i++)
System.out.print(a[i] + ",");
System.out.println();
}
}
下面是本人的一次运行结果:
冒泡排序:
2348
冒泡排序优化:
2660
选择排序:
250
插入排序:
907
希尔排序:
12
归并排序:
7
归并排序优化:
5
快速排序:
6
三向切分快速排序:
15
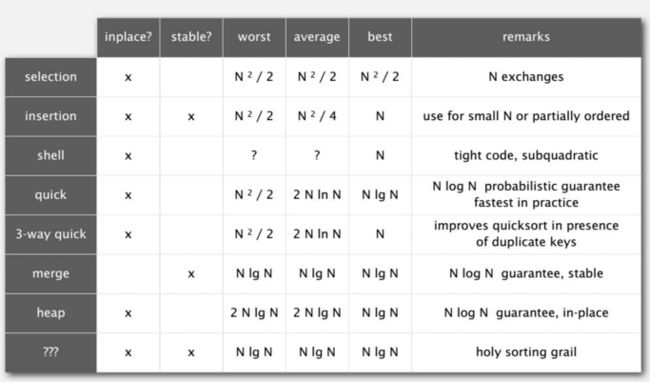
推荐一个很好的网站,对各种算法进行了总结,和动画描述:sorting-algorithms