各种基本算法实现小结（七）—— 常用算法

各种基本算法实现小结（七）—— 常用算法

（均已测试通过）

======================================================================

1、判断素数

测试环境：VC 6.0 (C)

 #include <stdio.h>
 #include <math.h>
 int is_sushu(int n)
 {
     int i, mid;
     mid=(int)sqrt(n);
     for(i=2; i<=mid; i++)
         if(0 == n%i)
             return 0;
     return 1;
 }
 void main()
 {
     int n;

     printf("Enter a num: ");
     scanf("%d", &n);
     if(is_sushu(n))
         printf("%d is sushu!/n", n);
     else
         printf("%d is not sushu.../n", n);
 }

运行结果：

    

==========================================================

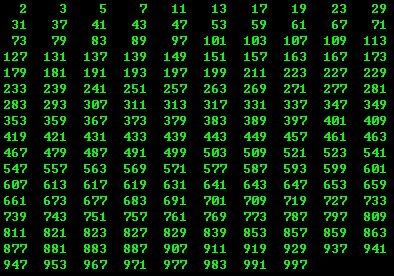
2、 求2-1000之间的所有素数

测试环境：VC 6.0 (C)

 #include <stdio.h>
 #include <math.h>
 #define MAX 1000
 int is_sushu(int n)
 {
     int i, mid;
     mid=(int)sqrt(n);
     for(i=2; i<=mid; i++)
         if(0 == n%i)
             return 0;
     return 1;
 }
 void main()
 {
     int i, count;

     count=0;

     for(i=2; i<=MAX; i++)
         if(is_sushu(i))
         {
             count++;
             printf("%5d", i);
                 if(0 == count%10)
                     printf("/n");
         }
     printf("/n");
 }

运行结果：

==========================================================

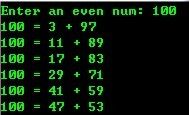
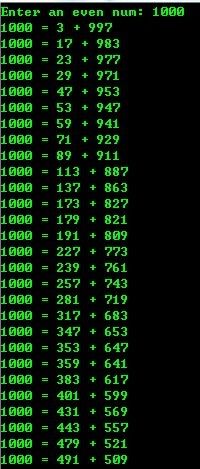
3、 验证哥德巴赫猜想

哥德巴赫猜想：任意一个大于等于6的偶数都可以分解为两个素数之和

如： 6 = 3+3；100 = 3+97=11+89； 1000 = 3+997=59+941=。。。

 

测试环境：VC 6.0 (C)

 #include <stdio.h>
 #include <math.h>
 #define MAX 1000
 int is_sushu(int n)
 {
     int i, mid;
     mid=(int)sqrt(n);
     for(i=2; i<=mid; i++)
         if(0 == n%i)
             return 0;
     return 1;
 }
 void main()
 {
     int i, mid, n;

     printf("Enter an even num: ");
     scanf("%d", &n);

     mid=n/2;
     for(i=2; i<=mid; i++)
     {
         if(is_sushu(i) && is_sushu(n-i))
             printf("%d = %d + %d/n", n, i, n-i);
     }

 }

运行结果：

       

==========================================================

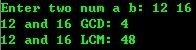
4、 求最大公约数（GCD）和最小公倍数(LCM)

测试环境：VC 6.0 (C)

 #include <stdio.h>
 void  max_min(int &m, int &n)
 {
     int tmp;
     if(m<n)
     {
         tmp=m;
         m=n;
         n=tmp;
     }
 }
 int Cal_GCD(int m, int n)
 {
     int gcd;

     max_min(m, n);
     gcd=m%n;
     while(gcd)
     {
         m=n;
         n=gcd;
         gcd=m%n;
     }
     return n;
 }
 void main()
 {
     int m, n, gcd;

     printf("Enter two num a b: ");
     scanf("%d %d", &m, &n);
     gcd=Cal_GCD(m, n);
     printf("%d and %d GCD: %d/n", m, n, gcd);
     printf("%d and %d LCM: %d/n", m, n, m*n/gcd);
 }

运行结果：

==========================================================

5、统计个数（数字）

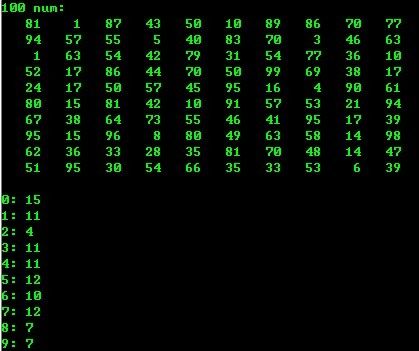
用随机函数产生100个[0，99]范围内的随机整数，

统计个位上的数字分别为0，1，2，3，4，5，6，7，8，9的数的个数并打印出来

测试环境：VC 6.0 (C)

 #include <stdio.h>
 #include <stdlib.h>
 #include <time.h>
 #include <string.h>
 #define MAX 101
 void input(int num[])
 {
     int i;
     srand((unsigned)time(NULL));
     for(i=1; i<MAX; i++)
         num[i]=rand()%100;
 }
 void output(int num[])
 {
     int i;
     for(i=1; i<MAX; i++)
     {
         printf("%5d", num[i]);
         if(0==i%10)
             printf("/n");
     }
     printf("/n");
 }
 void cal_num(int num[], int count[])
 {
     int i, mod;

     for(i=1; i<MAX; i++)
     {
         mod=num[i]%10;
         count[mod]++;
     }
 }
 void main()
 {
     int num[MAX];
     int i, count[10];

     memset(count, 0, 10*sizeof(int)); /* initial count[] to 0 */
     input(num);
     printf("100 num:/n");
     output(num);

     cal_num(num, count);
     for(i=0; i<10; i++)
         printf("%d: %d/n", i, count[i]);
 }

运行结果：

==========================================================

6、统计个数（数字、字符、其它字符）

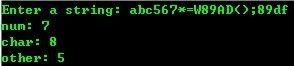
输入一行字符，统计其中有多少个数字、字符和其它字符

测试环境：VC 6.0 (C)

 #include <stdio.h>
 #include <string.h>
 #define MAX 1024
 void cal_num(char *str, int count[])
 {
     char *pstr;
     pstr=str;
     while(*pstr) /* *pstr != 0 */
     {
         if(*pstr>='0' && *pstr<='9')
             count[0]++;
         else if((*pstr>='a' && *pstr<='z') || (*pstr>='A' && *pstr<='Z'))
             count[1]++;
         else
             count[2]++;

         pstr++;
     }
 }
 void main()
 {
     char str[MAX];
     int i, count[3];  /* 0->num; 1->char; 2->others */
     memset(count, 0, 3*sizeof(int));

     printf("Enter a string: ");
     scanf("%s", str);
     cal_num(str, count);
     for(i=0; i<3; i++)
     {
         switch(i)
         {
             case 0:
                 printf("num: %d/n", count[i]);
                 break;
             case 1:
                 printf("char: %d/n", count[i]);
                 break;
             case 2:
                 printf("other: %d/n", count[i]);
                 break;
         }
     }
 }

运行结果：

==========================================================

7、 数制转换（递归实现）

本算法仅实现了基数为2-16的数制转换

如果大家希望扩展范围，仅需要对基数表示字符case 进行扩展即可，如G、H、I ...

测试环境：VC 6.0 (C)

 #include <stdio.h>
 int flag=1; /* check: n/d == 0 */
 void trans_num(int n, int d)
 {
     int mod;
     mod=n%d;
     n=n/d;
     while(flag && n)
         trans_num(n,d);
     flag=0;
     switch(mod)
     {
         case 10:
             printf("A");
             break;
         case 11:
             printf("B");
             break;
         case 12:
             printf("C");
             break;
         case 13:
             printf("D");
             break;
         case 14:
             printf("E");
             break;
         case 15:
             printf("F");
             break;
         default:
             printf("%d", mod);
     }

 }
 void main()
 {
     int n, d;
     printf("Enter n d: ");
     scanf("%d %d", &n, &d);

     trans_num(n, d);
     printf("/n");
 }

运行结果：

         

 

算法改进

数制直接转为字符输出，扩展支持16进制以上的数制转换

 #include <stdio.h>
 int flag=1; /* check: n/d == 0 */
 void trans_num(int n, int d)
 {
     int mod;
     mod=n%d;
     n=n/d;
     while(flag && n)
         trans_num(n,d);
     flag=0;
     if(mod>=10)
         mod=mod-10+65;  /* convert to char */
     else
         mod=mod+48;
     printf("%c", mod);  /* print char (%c) */
 }
 void main()
 {
     int n, d;
     printf("Enter n d: ");
     scanf("%d %d", &n, &d);

     trans_num(n, d);
     printf("/n");
 }

运行结果（扩展进制）：

                

100 = 4*24+4            1000=1*24*24+17*24+16  10000=17*24*24+8*24+16        1000=27*36+28

==========================================================

8、 数制转换（栈实现）

 

核心思想和递归实现类似，都是压栈的原理，实现较简单，请自己尝试实现

==========================================================

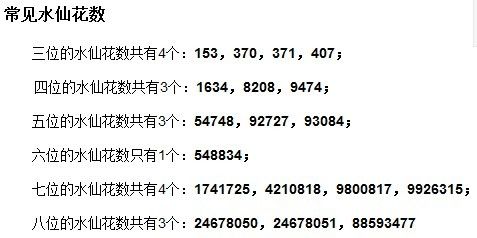
9、 水仙花数

水仙花数简述： 水仙花数是指一个 n 位数 ( n≥3 )，它的每个位上的数字的 n 次幂之和等于它本身。

如：153=1^3+5^3+3^3（3位数）；1634=1^4+6^4+3^4+4^4（4位数）；54748=5^5+4^5+7^5+4^5+8^5（5位数）

 

判断任一3位数，是否为水仙花数

测试环境：GCC

 #include <stdio.h>
 main()
 {
     int b, s, g, n, sum;
     scanf("%d", &n);
     b=n/100;
     s=n/10%10;
     g=n%10;
     sum=b*b*b+s*s*s+g*g*g;
     if(sum==n)
         printf("Yes/n");
     else
         printf("No/n");
 }

运行结果（Redhat Linux）：

================================================

求4位数的水仙花数（1000<=X<=9999）

测试环境：VC 6.0 (C)

 #include <stdio.h>
 int main()
 {
     int i,j,k,l,m,n;
     for(i=1; i<=9; i++)
         for(j=0; j<=9; j++)
             for(k=0; k<=9; k++)
                 for(l=0; l<=9; l++)
                     if((i*1000+j*100+k*10+l)==i*i*i*i+j*j*j*j+k*k*k*k+l*l*l*l)
                         printf("%d%d%d%d=%d^4+%d^4+%d^4*%d^4/n", i, j, k, l, i, j, k, l);
     return 0;
 }

运行结果：

================================================

思考：如果求得高精度大数的水仙花数，如8位、18位、28位的水仙花数（需考虑计算机精度，可采用数组或指针实现，大数计算）

==========================================================

10、 大数计算

大数运算：参加的值和计算结果通常是以上百位数，上千位数以及更大长度之间的整数运算，早已超出了计算机能够表示数值的精度范围（2^32=4294967296或2^64=18446744073709551616）即64位机最大也才20位，因此需要想出其它的办法计算大数。

 

求任意两整数之和（1000位以内）

测试环境：VC 6.0 (C)

 #include <stdio.h>
 #include <string.h>
 #define MAX 1000 /* precision */
 void input(char ch[])
 {
     scanf("%s", ch);
 }
 void add(char ch1[], char ch2[], char ch3[])
 {
     int len1, len2, len3, maxlen;
     int sum, flag;
     len1=strlen(ch1);
     len2=strlen(ch2);
     len3=maxlen=len1 >= len2 ? len1 : len2;
     flag=0; /* jin wei */

     while(len1>=1 && len2>=1)
     {
         sum=ch1[len1-1]-'0' + ch2[len2-1]-'0' + flag; /* char -> int to calculate sum */
         flag=0;

         if(sum>=10)
         {
             sum-=10;
             flag=1;
         }
         ch3[maxlen-1]=sum + '0';
         len1--;
         len2--;
         maxlen--;
     }
     while(len1>=1) /* if num1[] is longer or maxer */
     {
         sum=ch1[len1-1]-'0' + flag;
         flag=0;

         if(sum>=10)
         {
             sum-=10;
             flag=1;
         }
         ch3[maxlen-1]=sum + '0';
         len1--;
         maxlen--;
     }

     while(len2>=1) /* if num2[] is longer or maxer */
     {
         sum=ch2[len2-1]-'0' + flag;
         flag=0;

         if(sum>=10)
         {
             sum-=10;
             flag=1;
         }
         ch3[maxlen-1]=sum + '0';
         len2--;
         maxlen--;
     }
     if(flag != 0) /* if flag, then print gaowei(jinwei) */
         printf("%d", flag);
     for(int i=0; i<len3; i++)
         printf("%c", ch3[i]);
     printf("/n");
 }
 int main()
 {
     char ch1[MAX], ch2[MAX], ch3[MAX+1];
     memset(ch3, '0', sizeof(ch3));
     input(ch1);
     input(ch2);
     add(ch1, ch2, ch3);
     return 0;
 }

运行结果：

    

思考：请大家自己设计实现更复杂的大数减法、乘法、除法，求余、求幂、求最小公倍数等大数运算（提示：可用数组或链表）

==========================================================

参考推荐：

学习算法之路

各种基本算法实现小结（一）—— 链 表

各种基本算法实现小结（二）—— 堆 栈

各种基本算法实现小结（三）—— 树与二叉树

各种基本算法实现小结（四）—— 图及其遍历

各种基本算法实现小结（五）—— 排序算法

各种基本算法实现小结（六）—— 查找算法

各种基本算法实现小结（七）—— 常用算法

12个有趣的C语言面试题

作者原文地址：http://blog.csdn.net/sunboy_2050/article/details/5645837