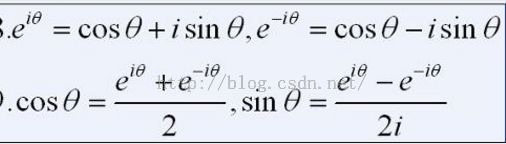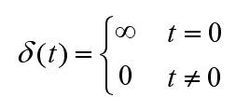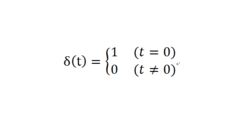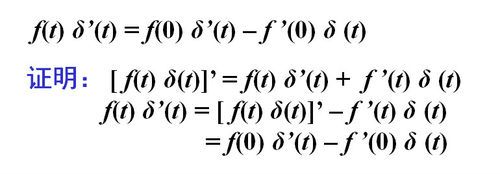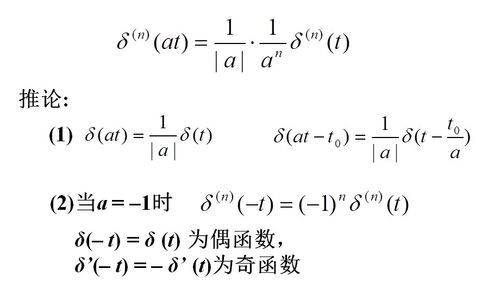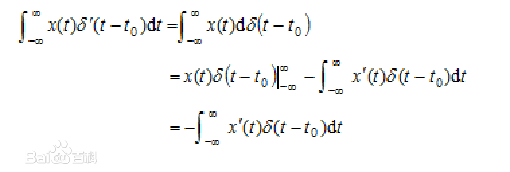信号与系统绪论

系统的概念不仅限于电路，通信，控制，还应当包括物理系统，非物理系统，人工系统，自然系统，通信系统，电路系统，~~网络等等

信号分类：

确定性信号，某一时刻，可确定函数值，称为确定性信号与规则信号

随机信号，不能给出确切的时间函数，只知道它的统计特性

周期信号，f(t)=f(t+nT)

非周期信号，可认为T趋于无穷大

混论信号：貌似随机而严格遵循规律的信号

连续时间信号与离散时间信号

一维信号，声压随时间变化的函数

多维信号,黑白图像每个像素点具有不同的光强度

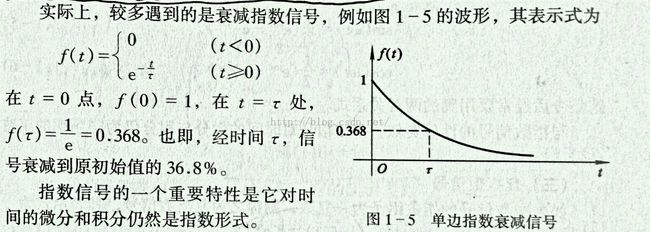
指数信号：

f(t)=K*e^(a*t)

τ=1/lal , τ越大，信号增长或衰减的速率越慢

正弦信号：

f(t)=K*sin(w*t+theta)

指数衰减正弦信号：K*e^(-a*t)*sin(w*t)

欧拉公式

复指数信号：

Sa(t)信号（抽样信号）

Sa(t)=sint/t

钟形信号（高斯信号）

信号运算

移位（时移和延时），反褶，尺度倍乘（压缩和拓展），微分和积分，相加和相乘

信号积分运算后效果和微分相反，信号突变的部分可变得平滑，可由此削弱信号中混入的毛刺（噪声）的影响

阶跃信号和冲激信号

单位斜变信号：

                        f(t)=0@(t<0),=t@(t>=0)

单位阶跃信号：

                        u(t)=0@(t<0),=1@(t>=0)

表示矩形脉冲：

符号函数

sgn(t)=1@(t>0),=-1@(t<0)

sgn(t)=2u(t)-1

单位冲激信号

δ(t)=lim[u(t+τ/2)-u(t-τ/2)]/τ    ~τ趋于0

类似的

冲激函数的定义为：

注：【现在在某些情况下也有用当t=0时，冲击函数的值取1，称单位冲击函数。在理解它的积分中比较好理解，而且目前大多数数字信号处理教材都采用值为1的形式】

通常，单位冲激函数由如下特殊的方式定义（由 狄拉克最早提出） ：

狄拉克定义

冲激函数与按某些信号取极限来定义是一致的

性质

筛选性质

如果信号x(t)是一个在t=t0处连续的普通函数，则有

上式表明，信号x(t)与冲激函数相乘，筛选出连续时间信号x(t)在t=t0时的函数值x(t0)。可以理解为冲激函数在t=t0时刻对函数x(t)的一瞬间的作用，其值是冲激函数和x(t0)相乘的结果，瞬间趋于无穷大。

取样性质

如果信号x(t)是一个在t=t0处连续的普通函数，则有

冲激信号的取样特性表明，一个连续时间信号x(t)与冲激函数相乘，并在(一∞，+∞)时间域上积分，其结果为信号x(t)在t=t0时的函数值x(t0)。该式可以理解为冲激函数作用于函数x(t)，趋于稳态时最终作用的结果，即得到信号x(t)在t0时刻的值x(t0)。

导数性质

冲激函数的导数性质及其证明如下图所示：

尺度变换

冲激函数的尺度变换及其推论明如下图所示：

积分性质

冲击偶信号

冲激偶信号即冲激函数的微分（阶跃函数的二阶导数）将呈现正、负极性的一对冲激，以δ'(t)表示。

冲激函数的微分（ 阶跃函数的二阶导数）将呈现正、负极性的一对冲激，成为冲激偶信号，以δ'(t)表示。可以利用规则函数系列取极限的概念引出δ'(t)，此处借助三角形脉冲系列。

如下图。三角形脉冲s（t）其底宽为2τ，高度是1/τ，当τ->0时，s（t）成为单位冲激函数δ(t)。

左下画出ds（t）/dt波形，它是正、负极性的两个矩形脉冲，称为脉冲偶对。其宽度均为τ，高度分别为1/(τ^2)和-1/(τ^2)。当τ->0时，ds（t）/dt是正负极性的两个冲激函数，其强度均为无限大，示于右下端，这就是冲激偶δ'(t)。

性质

编辑

设为常规函数，其导数在处连续，则积分

利用冲激函数的抽样性质，从上式得

这是冲激偶信号的一个重要性质，称为的抽样性质。

冲激偶信号的另一个性质是，它所包含的面积等于零，这是因为正、负两个冲激的面积相互抵消了。于是有

说明

冲激函数的各阶导数统称为高阶冲激。特别指出，在同一时刻出现的 单

位冲激函数、高阶冲激函数间的乘积没有意义。

信号的分解

1）直流分量与交流分量

直流分量即信号的平均值

信号的平均功率等于直流功率和交流功率之和

2）偶分量和奇分量

      信号的平均功率等于偶功率和奇功率之和

       3）脉冲分量

       一个信号可近似分解为许多脉冲分量之和

       4）实部分量和虚部分量——瞬时值为复数的信号

       5）正交函数分量

         正交函数集表示一个信号，例用各次谐波的正弦与余弦信号叠加表示矩形脉冲

       6）分形描述信号

自然界：云彩的边界，山地的轮廓，海岸线的分布，流体的湍流，粒子的布朗运动轨道等

应用：图像数据压缩，语音合成等

系统模型及其分类

连续时间系统与离散时间系统

数字计算机，RLC电路

即时系统与动态系统

电阻，电容电感磁芯寄存器（记忆元件和电路）

集总参数系统与分布参数系统

集总参数元件，分布参数元件（传输线，波导）

线性系统与非线性系统

时变系统与时不变系统

系统参数随不随时间变化

可逆系统与不可逆系统

输入与输出可不可逆，换言之是不是一一对应的函数关系

线性时不变系统

集总参数线性时不变系统—LTI—Llinear time-invariant

1）叠加性与均匀性

2）时不变系统

证明y（n）=2x（n）+3和y（n）=2x（n）+3n的线性与时不变性

y1(n)+y2(n)=2x1+2x2+6
T(x1+x2)=2x1+2x2+3 非线性
y(n-n0)=2x(n-n0)+3
T(x(n-n0))=2x(n-n0)+3时不变
y1(n)+y2(n)=2x1+2x2+6n
T(x1+x2)=2x1+2x2+3n 非线性
y(n-n0)=2x(n-n0)+3n-3n0
T(x(n-n0))=2x(n-n0)+3n时变

3）微分特性

4）因果特性

输出时刻只可能大于或等于输入时刻

因果系统，r1(t)=e1(t-1)

非因果系统，r2(t)=e2(t+1)

系统分析方法

系统模型建立：

输入-输出描述法—对于单输入单输出系统

状态变量描述法—对于多输入-多输出系统

系统模型求解：

1）时域分析

卷积方法，数值方法

2）变换域方法

傅里叶变换（FT）以频率为独立变量

拉普拉斯变换（LT）注重极点和零点分析，利用s域和z域的特性

离散系统分析的正交变换（离散傅里叶变换DFT，离散沃尔什变换DWT等）

实际问题的解决—信号传输和处理研究领域

人工神经网络，模糊集理论，遗传算法，混沌理论等相互结合解决线性时不变系统模型的难题