Sicily 1527. Tiling a Grid With Dominoes
题意:
问一个 L*4 的矩形,用2*1的小矩形组成有多少种组法。
思路:
递推。用一个4bit的整数表示“行状态”。写出15个递推式即可。
首先,定义 f [ i ] [ j ] 为, 已组成长度 (i - 1)* 4 的完美矩形, 第 i 行的状态是 j (0~15)的方案数。那么我们可以考察 f [ i ] [ j ] 可以怎么求得。
注意下面的状态方程的推导,围绕的思路不仅是要填满 15(1111) 这个“满”状态,而是要填满所有1~15的状态( i 行才能根据 i - 1 行转移),所以2情况和5情况,不是重复的,动态规划里所有的一切都是围绕“状态”的概念来展开。
1. 【竖放】首先,如果在 i - 1 行有缺某些位,放上一块(竖着放)之后, i-1行的该位被填上,而i行的该位会突出,状态码刚好是对15(1111)取补。例如
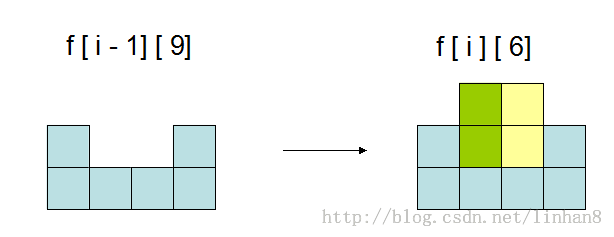
2. 【横放】假设 i - 1 行已经完美覆盖,那么我们总可以在 i 行 横放 1块或2块积木来得到新的状态。例如
f [ i ][ 6 ] 、 f [ i ][ 12 ] 与 f [ i ][ 3 ] 情况类似,图就不赘画了。
3. 如果经过前述 i 行 有突出一个位的, 我们还可以通过横放一个积木补上来将其填得更满,例如:
注意是在同一行(i行)横放积木,所以第一个下标全是 i , 其余情况类似,不画。
直到这里,我们把 0 ~ 14 的状态都填好了,接下来考虑最终极的, 15(1111,满行)状态的情况。
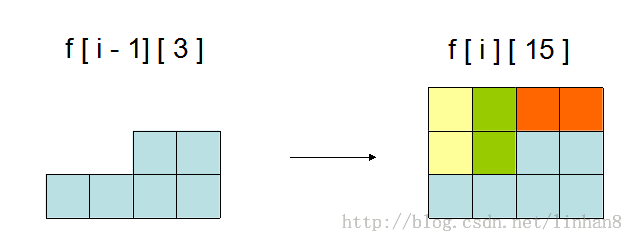
4. i - 1 行缺 连2位 的情况(0011 = 3, 1001 = 9, 1100 = 12),可以通过放置2个竖的积木和1个横的积木达到完美,例如
其他2种情况不再赘画。
5. i - 1 行如果已经是满的,我们直接横放2个积木,i 行也满,这种不用画了吧。
代码:
// Problem#: 5855
// Submission#: 1456823
// The source code is licensed under Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
// URI: http://creativecommons.org/licenses/by-nc-sa/3.0/
// All Copyright reserved by Informatic Lab of Sun Yat-sen University
#include <stdio.h>
#define maxx 10000
#define maxw 1000
int f[maxx+9][1<<4] ; //
int main () {
int L,n ;
f[1][0] = f[1][3] = f[1][6] = f[1][12] = f[1][15] = 1 ;
for ( int i = 2 ; i <= maxw ; ++i ) {
// 竖放 1
for ( int j = 0 ; j <= 15 ; ++j ) {
f[i][j] = f[i-1][15-j] ;
}
// 横放 2
f[i][3] += f[i-1][15] ;
f[i][6] += f[i-1][15] ;
f[i][12] += f[i-1][15] ;
// 横加竖 3
f[i][7] += f[i][4] + f[i][1] ;
f[i][14] += f[i][8] + f[i][2] ;
// 混合型 4 ( 2竖1横 )
f[i][15] += f[i-1][3] + f[i-1][6] + f[i-1][12] ;
// 混合型 5 ( 2横 )
f[i][15] += f[i-1][15] ;
}
scanf ( "%d" , &n ) ;
for ( int cas = 1 ; cas <= n ; ++cas ) {
scanf ( "%d" , &L ) ;
printf ( "%d %d\n" , cas , f[L][15] ) ;
}
}