分类器的相关概念

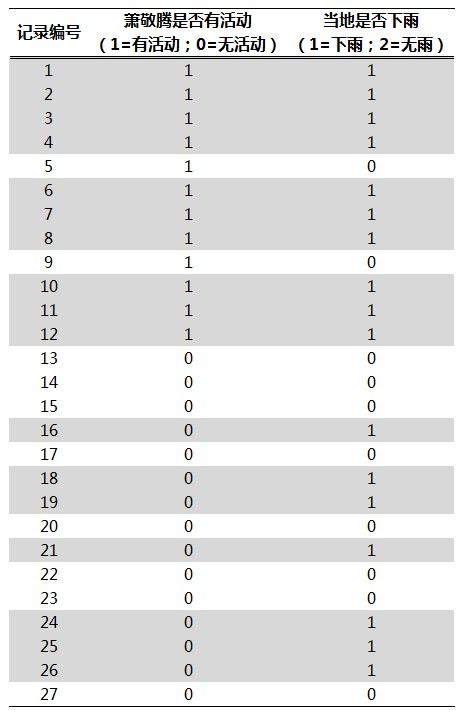
昨天，@人民网 发了一条八卦微博，盘点“雨神”（@萧敬腾）是如何炼成的。微博称，网友统计发现，在@萧敬腾 近年12次主要行程中，有10次他的“现身”让当地下起了雨，下雨的概率为83.3%。

图1

这里，网友相当于是做了一个人工数据挖掘，用术语表示，就是构造了如下一个分类器：

IF 萧敬腾有活动THEN当地下雨 ELSE 当地不下雨 END

该分类器预测老萧举办个唱或发售新专辑的城市会下雨的概率为83.3%。

借助老萧的神威，我们来总结下分类器的相关概念。

分类器是数据挖掘中对样本进行分类的方法的统称，包含决策树、逻辑回归、朴素贝叶斯、神经网络等算法。分类器的构造和实施大体会经过以下几个步骤：

• 选定样本（包含正样本和负样本），将所有样本分成训练样本和测试样本两部分。
• 在训练样本上执行分类器算法，生成分类模型。
• 在测试样本上执行分类模型，生成预测结果。
• 根据预测结果，计算必要的评估指标，评估分类模型的性能。

以上的描述中已经提到了分类器所涉及的一些概念：训练样本、测试样本、正样本、负样本。此外，还有未涉及到的概念，如样本的特征变量和类标识变量，以及常见的评估工具、指标，包括混淆矩阵、准确率、覆盖率、命中率、ROC、AUC、Lift、Gain、K-S等。本文介绍评估指标中的准确率、覆盖率和命中率。

本文不涉及样本训练的过程，假定分类器已经存在，并且有下面的数据集作为测试样本：

图2

该测试样本集的前12条记录，就是雨神所到之处的降雨记录；后15条记录是随机选取的同一时期相关城市在老萧没有活动情况下的降雨记录。“萧敬腾是否有活动”是特征变量，1表示有活动，0表示无；“当地是否下雨”是类标识变量，1表示下雨，0表示无雨。由于我们的研究目标倾向于预测下雨的可能性，因此我们选定“当地是否下雨=1”的样本为正样本（图2中灰底的记录）；相应的，“当地是否下雨=0”的样本为负样本。当我们考察的类标识变量是个二值变量时，通常我们会把感兴趣的那个取值对应的样本称作正样本，而另一个值对应的样本则称作负样本。比如在识别欺诈客户时，我们感兴趣的是这类客户是否被我们识别出来，这样我们会把欺诈客户作为正样本看待，而把正常客户当作负样本。

现在，我们把网友构造的分类器描述的规范一些：

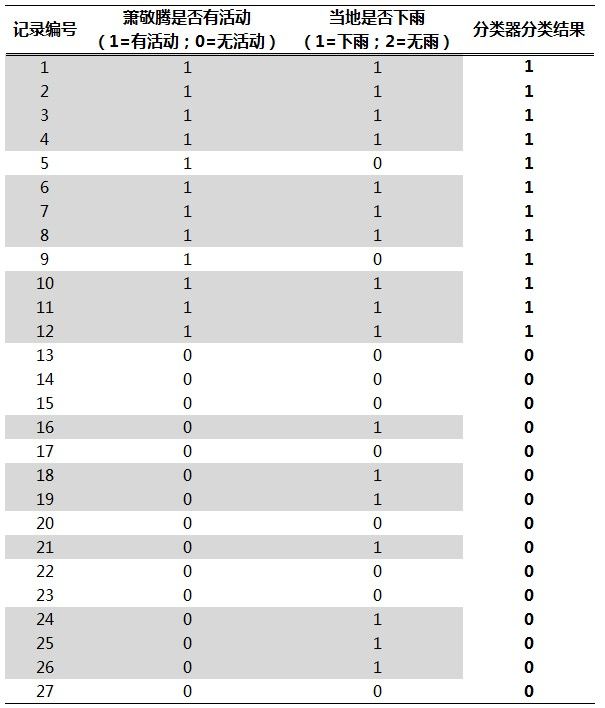
IF萧敬腾是否有活动=1THEN 当地是否下雨=1 ELSE 当地是否下雨=0END

这个分类器在图2样本上的分类结果是：

图3

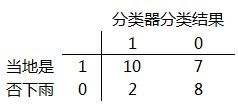
根据分类结果，我们可以计算出该分类器的混淆矩阵：

图4

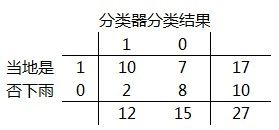
所谓混淆矩阵（Confusion Matrix），是一种比较分类器分类结果和类标识变量实际值的矩阵，其中的每一行代表了分类器的分类结果，每一列则表示类标识变量的实际值。为方便说明，我们把图4的混淆矩阵扩充一下，计算每一行和每一列的和，见图5：

图5

在图5中，每一行的和为17、10，分别代表17个正样本和10个负样本；每一列的和为12、15，表示分类器判定出“当地是否下雨=1”的数量为12，“当地是否下雨=0”的数量为15。矩阵中包含4个元素，以第一行的两个元素10和7为例，它们表示在所有实际“当地是否下雨=1”的17条记录中，被分类器正确判定为“当地是否下雨=1”的数量为10，错误判定为“当地是否下雨=0”的记录数为7；也就是针对17条下雨记录，分类器准确判断了其中10条，误判了7条。再来看列元素的含义，第一列的两个元素10和2表示，在分类器判定出的12条“当地是否下雨=1”的记录中，10条为正确判断，2条为误判（实际没有下雨）。

根据混淆矩阵，我们可以计算一系列指标来评估分类器的性能。

（1）准确率

准确率是针对整个分类结果而言的，计算公式为：

准确率 = 正确预测的样本数 / 样本总数 * 100%

从图5我们可以算出：准确率 = (10+8) / 27 * 100% = 66.7%

与准确率相对应的是不常用的错误率，计算公式为：

错误率 = 错误预测的样本数 / 样本总数 * 100%

根据图5计算得：错误率 = (2+7) / 27 * 100% = 33.3%

可见，错误率 = 1 - 准确率。

分类器的第一目标往往是保证准确率，特别在你需要对识别出来的记录做一些敏感操作时。

（2）覆盖率

覆盖率是分别针对正负样本而言的，计算公式为：

正（负）样本覆盖率 = 正确预测的正（负）样本数 / 实际正（负）样本总数 * 100%

以图5为例，我们有：

正样本覆盖率 = 10 / 17 * 100% = 58.8%

负样本覆盖率 = 8 / 10 * 100% = 80%

在雨神这个case中，正样本覆盖率描述了，在17条下雨记录中，被分类器正确识别出来的比率。在商业实践中，有时候我们的目标是使分类结果具有较高的正样本覆盖率。比如在一次电子邮件营销中，我们欲针对具有某类特征的客户发送营销邮件，这个时候我们会要求模型尽可能把所有具有该特征的客户都识别出来。其副作用是，某些不具有我们所需特征的用户，也有较大的可能进入我们的Email发送列表，从而降低结果的准确率。但这影响似乎不大，非目标客户收到你的邮件他一笑置之便是，而你多发送几封邮件的边际成本也很低。

（3）命中率

命中率同样是针对正负样本而言的，刚好与针对行操作的覆盖率相对，命中率是在列上操作。计算公式为：

正（负）样本命中率 = 正确预测的正（负）样本数 / 预测出的正（负）样本总数 * 100%

在图5中，

正样本命中率 = 10 / 12 * 100% = 83.3%

负样本命中率 = 8 / 15 * 100% = 53.3%

命中率描述了，当你使用该分类器来做预测时，其预测正确的概率。在雨神case中，现在假设你根据萧敬腾到某个城市活动，来预测当地会下雨，那么你的预测“命中”的概率将会是83.3%。这样就是网友所说的“萧敬腾的现身让当地下雨的概率为83.3%”的含义。

分类器评估指标中的ROC、AUC、Lift、Gain和K-S等指标的介绍，已经超出了雨神case所能演示的范围。雨神也是有其局限性的，但不管怎样，求求老萧来趟杭州吧，都热了一个月了！