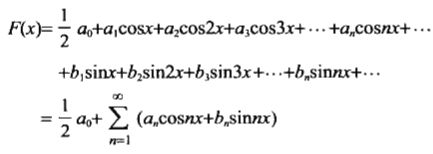傅里叶级数的理解

傅里叶级数的理解

三角函数的基本形式是
f(x) = Asin(nx+Θ)
A:振幅
n:频率
Θ:相位
x也可以用wt来表示

函数的正交：两个函数的积的积分为0,那么这两个函数为正交关系
1.当n!=m时,cosnx与cosmx正交,sinnx与cosmx正交, sinnx与sinmx正交
2.当n=m时,cosnx与cosmx不正交,sinnx与cosmx正交, sinnx与sinmx不正交
即sinnx,cosnx都与自身不成正交

相互正交的函数可以组合出不同的函数

当sin函数和cos函数随机组合相加时
例如f(x)=Asinnx+Bcosmx
A和B决定了f(x)的振幅和相位
n和m决定了f(x)波形和频率 为
2π(2π/n)和(2π/m)的最小公倍数

通过cos sin函数的相加可以组合出不同的相位和幅度 类似于矢量 的运算
如 sinx+cosx = 2√sin(x+45°)
相比之下用sin(x+Θ)表示就复杂许多 不利于分解

傅里叶解析就是求原波是由哪些频率和振幅的波组合而成
首先来看公式

意思就是原波形可以由若干个sin或者cos函数合成
也可以是全部都是sin也可以全部是cos cos和sin的数目不一定相等
a0,a1,b0,b1….称为傅里叶系数

那么如何分解出波呢?
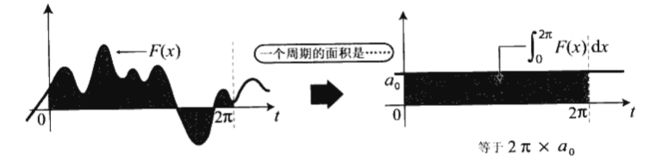
1.首先要取出原波最小周期的部分进行分析
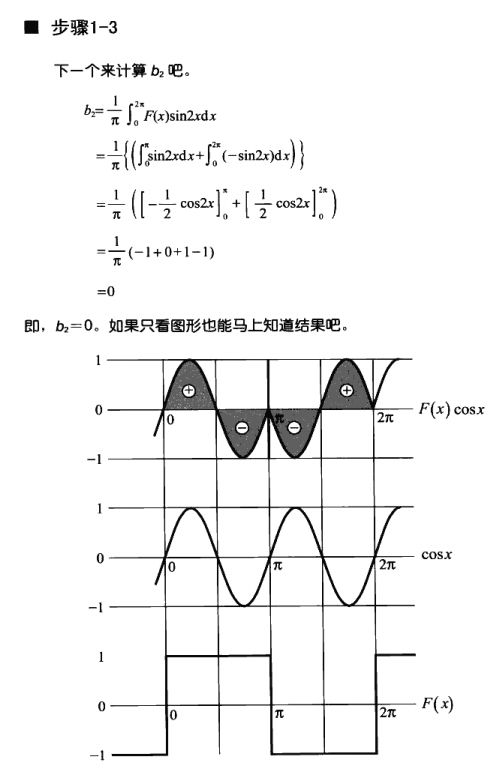
2.然后过滤 分解出各类的波的振幅 应该这么做:
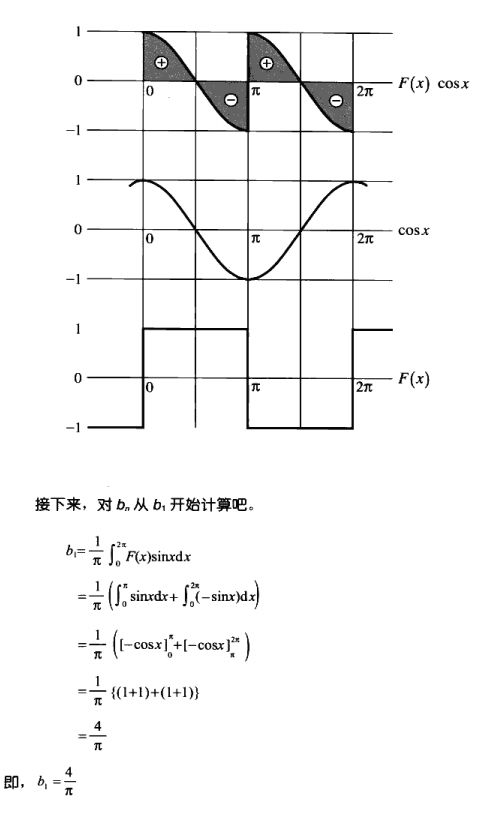
由于sinnx,cosnx都与自身不成正交 也就是积的积分值为0 那么F(x)乘以cosnx的积分结果就剩下ancosnx*cosnx的积分值
由于cosnx*cosnx的积分结果是π所以可以求出an
bn同理

至于a0是因为原来的波抵消了大部分的波峰和波谷还剩下一些面积
填平后就是右下图黑色部分了

此外也可以把cos0像之前一样与F(x)相乘求积分 由于得到的结果是2πa 还要除以2
3.分解出频率
根据an,bn求出rn的大小 然后按照n的从小到大顺序排列,得到频率谱

来看个例题







这应该也算是该公式的推导吧
题外话:

1.sin(x)+0.5*sin(2*x)+(1/3)*sin(3*x)+(1/4)*sin(4*x)+(1/5)*sin(5*x)+(1/6)*sin(6*x)+(1/7)*sin(7*x)+(1/8)*sin(8*x)+(1/9)*sin(9*x)+(1/10)*sin(10*x)+(1/11)*sin(11*x)+(1/12)*sin(12*x)+(1/13)*sin(13*x)

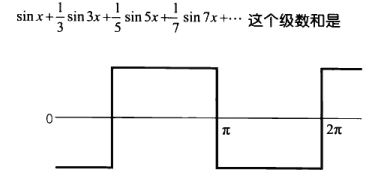
2.sin(x)+(1/3)*sin(3*x)+(1/5)*sin(5*x)+(1/7)*sin(7*x)

可以直接百度以上两个函数 你会看到有趣的图像

以上部分截图来自《漫画傅里叶解析》