matlab曲面颜色

转载自

http://mirlab.org/jang/books/matlabProgramming4beginner/04-3_colorControl.asp?title=4-3%20%A6%B1%AD%B1%C3C%A6%E2%AA%BA%B1%B1%A8%EE

4-3 曲面顏色的控制

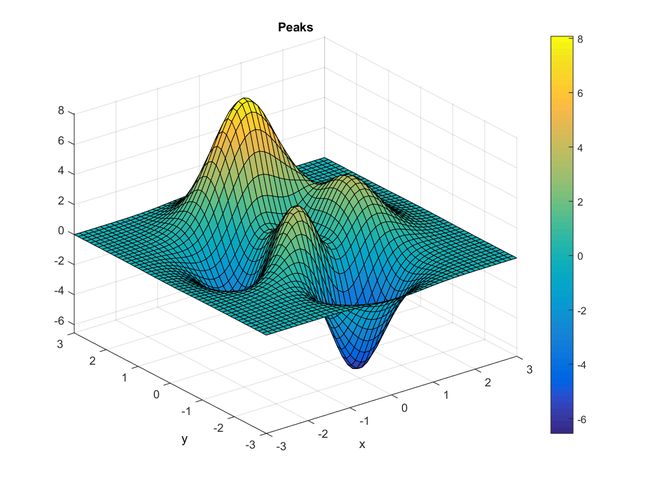
利用 colorbar 指令，可顯示 MATLAB 如何以不同顏色來代表曲面的高度，例如若先輸入「peaks」，再輸入「colorbar」，就可以得到下列圖形：

Example 1: 04-三維立體繪圖/colorbar01.m

peaks;colorbar;

 z =  3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...    - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...    - 1/3*exp(-(x+1).^2 - y.^2)  

如上圖所示，colorbar 可以顯示高度與顏色的對照長條圖，而曲面上每一個小方塊的顏色即根據此對照圖而得出。事實上，顏色與高度的對應關係是由一個「顏色對應表」（Colormap，或簡稱「色表」或「色盤」）來控制，此表是一個 m×3 的矩陣，m 的值通常是 64，代表真正用到的顏色個數，而每一列代表一個顏色的 RGB 值，一些常用的值可列表如下：

顏色	Red（紅色）	Green（綠色）	Blue（藍色）
black（黑）	0	0	0
white（白）	1	1	1
red（紅）	1	0	0
green（綠）	0	1	0
blue（藍）	0	0	1
yellow（黃）	1	1	0
magenta（錳紫）	1	0	1
cyan（青藍）	0	1	1
gray（灰）	0.5	0.5	0.5
dark red（暗紅）	0.5	0	0
copper（銅色）	1	0.62	0.4
aquamarine（碧綠）	0.49	1	0.83

MATLAB 預設的顏色對應表可由 colormap 得知，如下：

Example 2: 04-三維立體繪圖/colormap01.m

cm=colormap;size(cm)

ans =    64     3

由上可知 cm 是一個 64×3 的矩陣，因此 MATLAB 在畫圖時，會把 cm 第一列的顏色設定給曲面的最高點，把 cm 的最後一列的顏色設定給曲面的最低點，其餘高度的顏色則依線性內插法來決定。因此，我們只要改變顏色對應表，即可得到不同顏色的曲面。欲改變顏色對應表，也是用 colormap 指令，如下：

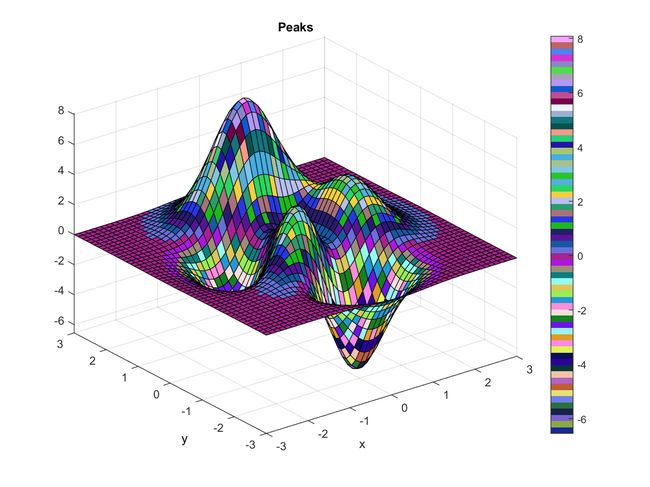
Example 3: 04-三維立體繪圖/plotxyz13.m

peaks;colormap(rand(64,3));colorbar;

 z =  3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...    - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...    - 1/3*exp(-(x+1).^2 - y.^2)  

在上述範例中，我們使用亂數來產生一個 64×3 顏色對應表，因此曲面看起來並不是很賞心悅目。事實上，要產生一個好看的顏色對應表並不是件容易的事，因此 MATLAB 有一些現成的顏色對應表，整理如下：

指令	說明
colormap hsv	HSV 的顏色對應表（預設值）
colormap hot	代表“熱”的顏色對應表
colormap cool	代表“冷”的顏色對應表
colormap summer	代表“夏天”的顏色對應表
colormap gray	代表“灰階”的顏色對應表
colormap copper	代表“銅色”的顏色對應表
colormap autumn	代表“秋天”的顏色對應表
colormap winter	代表“冬天”的顏色對應表
colormap spring	代表“春天”的顏色對應表
colormap bone	代表“X光片”的顏色對應表
colormap pink	代表“粉紅”的顏色對應表
colormap flag	代表“旗幟”的顏色對應表

例如，要使您的曲面使用感覺較冷的顏色，可輸入如下：

Example 4: 04-三維立體繪圖/plotxyz14.m

peaks;colormap cool; colorbar

 z =  3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...    - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...    - 1/3*exp(-(x+1).^2 - y.^2)  

除了以高度來設定顏色之外，surf 及 mesh 指令都可以接受第 4 個輸入引數來作為設定顏色的依據。例如，若要以曲面的斜率（即「梯度」或「Gradient」）來設定顏色，可進行如下：

Example 5: 04-三維立體繪圖/plotxyz15.m

[X, Y, Z] = peaks;surf(X, Y, Z, gradient(Z));axis tight;colormap hot

在上例中，gradient (Z) 會根據數值微分（Numerical Differentiation）來產生矩陣 Z 的梯度，surf 即利用此梯度來產生曲面的顏色。欲知 gradient 的詳細資訊，可在 MATLAB 指令視窗下輸入 help gradient。

若要以曲面的曲率來設定顏色，可進行如下：

Example 6: 04-三維立體繪圖/plotxyz16.m

[X, Y, Z] = peaks;surf(X, Y, Z, del2(Z));axis tight;colormap hot

在上例中，del2 (Z) 根據數值微分來產生矩陣 Z 的 discrete Laplacian，詳情可參見 help del2 傳回的線上支援。

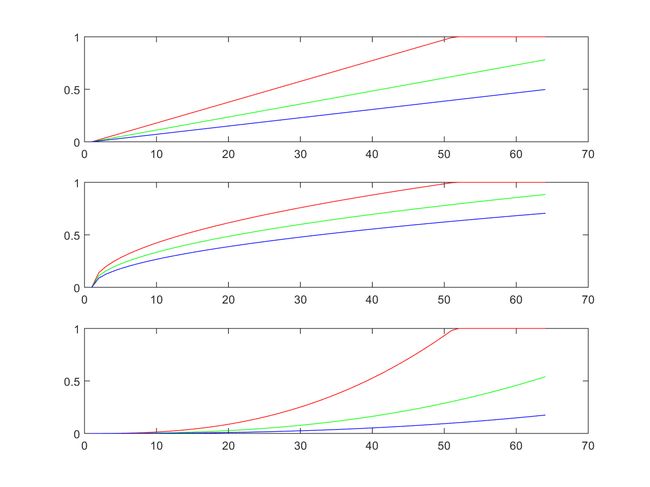
我們可用 brighten 指令來使顏色對照表變亮或變暗，如下：

Example 7: 04-三維立體繪圖/plotxyz17.m

colormap coppersubplot(3, 1, 1); rgbplot(colormap);brighten(colormap, 0.5)subplot(3, 1, 2); rgbplot(colormap);brighten(colormap, -0.8)subplot(3, 1, 3); rgbplot(colormap);

其中 rgbplot 可畫出 R、G、B 三色的比重對列數的變化。

上述 MATLAB 決定顏色的方法稱為「索引顏色」（Indexed Color）法，因為曲面上每個方塊先對應至顏色對應表的索引（即某一特定列），再由此列決定真正要用的顏色。如果您的顯示器能支援 24 位元全彩，則我們可以直接定義一千六百萬（224）種顏色，而不需要再定義顏色對應表。此種方法稱為「真實顏色」（True Color）法，如下：

Example 8: 04-三維立體繪圖/plotxyz18.m

Z = peaks(50);C(:, :, 1) = rand(50);	% C(:,:,1) 代表 R（Red，紅色）的份量C(:, :, 2) = rand(50);	% C(:,:,2) 代表 G（Green，綠色）的份量C(:, :, 3) = rand(50);	% C(:,:,3) 代表 B（Blue，藍色）的份量surf(Z, C);axis tight

在上圖中，曲面上每一個小方塊的顏色都是由矩陣 C 的 R、G、B 份量來決定，這就是「真實顏色」，而和前述的「索引顏色」有所不同。

在前述的例子中，每一個曲面都可以視為由一塊塊的四角小「瓷磚」所拼成，而且每一塊「瓷磚」表面的顏色是均勻一致的，其顏色值由「瓷磚」所在的曲面高度所決定。若要使「瓷磚」表面的顏色產生連續性的變化，可使用 shading 指令，例如我們可以先輸入「peaks」，再輸入「shading interp」，就可以得到下列顏色漸進變化的圖形：

Example 9: 04-三維立體繪圖/shadingInterp01.m

peaks;colormap jet;colorbar;shading interp;

 z =  3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...    - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...    - 1/3*exp(-(x+1).^2 - y.^2)  

由上圖可看出，經由 shading interp 的作用，曲面的顏色更加柔順平滑。有關 shading 指令的用法，可列表如下：

指令	說明
shading interp	使用 Bilinear Interpolation 來使「瓷磚」根據四頂點的顏色產生連續的變化
shading flat	「瓷磚」的顏色是均勻一致的。
shading faceted	「瓷磚」的顏色是均勻一致的，而且同時顯示「瓷磚」交接的「邊」。（此為預設值）

使用 colormap 及 shading，可產生意想不到的結果，例如：

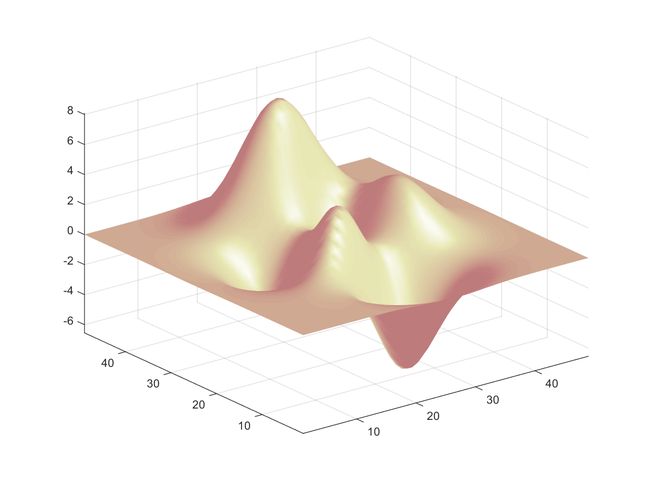
Example 10: 04-三維立體繪圖/plotxyz19.m

surfl(peaks);			% 曲面圖加上光源  axis tightcolormap(pink);shading interp

上圖的曲面，是否很像一件光滑無瑕的雕塑品呢？！