三维凸包之增量算法
算法工作过程:
选取点集中的四个点构成一个初始的四面体:
选两个点p1, p2,再选一个点p3,p3和p1, p2不在同一条直线上,这样形成了一个面。再选一个点,不在同一个面上,形成一个四面体。
然后继续研究剩余的点:
点在四面体内部,略过。
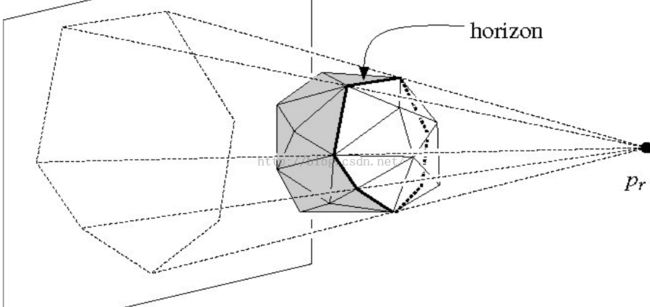
点在四面体外部,删除此点能“看见”的面,扩大凸包体积。
POJ 3528 Ultimate Weapon
http://poj.org/problem?id=3528
大意:求解多面体表面积
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-7;
const int N=5e2+10;
struct point{
double x,y,z;
point(){ x=0; y=0; z=0; }
point(double _x,double _y,double _z):x(_x),y(_y),z(_z) {}
point operator -(const point other){
return point(x-other.x,y-other.y,z-other.z);
}
point operator *(const point other){
return point(y*other.z-z*other.y,-x*other.z+z*other.x,x*other.y-y*other.x);
}
double operator ^(const point other){ //点乘
return x*other.x+y*other.y+z*other.z;
}
};
struct ch3D{
struct fac{
int a,b,c; // 面上三点的编号
bool ok; // 是否属于凸包
};
int n; //初始点数
point P[N]; //初始点
int cnt; //凸包上的三角形
fac F[N*6]; // 被创建的面不超过6N
int vis[N][N];
double vlen(point v){
return sqrt(v.x*v.x+v.y*v.y+v.z*v.z);
}
double area(point p1,point p2,point p3){
return vlen((p2-p1)*(p3-p1)); // 三角形面积*2
}
double volumn(point p1,point p2,point p3,point p4){
return fabs((p2-p1)*(p3-p1)^(p4-p1)); //V的6倍
}
double pToPlane(point p,fac ff){ // 点在面的同向: +
point m=P[ff.b]-P[ff.a];
point n=P[ff.c]-P[ff.a];
point v=p-P[ff.a];
return m*n^v;
}
void deal(int p,int a,int b){
int f=vis[a][b];
fac add;
if(F[f].ok){
if(pToPlane(P[p],F[f])>eps) dfs(p,f); //在同侧,能看见
else {
add.a=b, add.b=a, add.c=p, add.ok=1;
vis[p][b]=vis[a][p]=vis[b][a]=cnt;
F[cnt++]=add;
}
}
}
void dfs(int p,int num){ // 维护凸包
F[num].ok=0; //删除能看见的面
deal(p,F[num].b,F[num].a);
deal(p,F[num].c,F[num].b);
deal(p,F[num].a,F[num].c);
}
bool same(int s,int e){ //判断两个面是否是同一个面
point a=P[F[s].a],b=P[F[s].b],c=P[F[s].c];
return fabs(volumn(a,b,c,P[F[e].a]))<eps
&& fabs(volumn(a,b,c,P[F[e].b]))<eps
&& fabs(volumn(a,b,c,P[F[e].c]))<eps;
}
void construct(){
cnt=0;
if(n<4) return ;
/************判断四点不共面*************/
bool jud=1;
// 两点在线
for(int i=1;i<n;i++) {
if(vlen(P[0]-P[i])>eps){
jud=0;
swap(P[1],P[i]);
break;
}
}
if(jud) return ;
jud=1;
// 三点在面
for(int i=2;i<n;i++){
if(vlen((P[0]-P[1])*(P[0]-P[i]))>eps){
swap(P[2],P[i]);
jud=0;
break;
}
}
if(jud) return ;
jud=1;
// 四点成体
for(int i=3;i<n;i++){
if(volumn(P[0],P[1],P[2],P[i])>eps){
swap(P[3],P[i]);
jud=0;
break;
}
}
if(jud) return ;
/*************************************/
fac add;
for(int i=0;i<4;i++){
add.a=(i+1)%4;
add.b=(i+2)%4;
add.c=(i+3)%4;
add.ok=1;
if(pToPlane(P[i],add)>0) swap(add.b,add.c);
vis[add.a][add.b]=vis[add.b][add.c]=vis[add.c][add.a]=cnt;
F[cnt++]=add;
}
for(int i=4;i<n;i++){
for(int j=0;j<cnt;j++){
if(F[j].ok && pToPlane(P[i],F[j])>eps){
dfs(i,j);
break;
}
}
}
int tmp=cnt;
cnt=0;
for(int i=0;i<tmp;i++){
if(F[i].ok){
F[cnt++]=F[i]; // cnt speed < i speed
}
}
}
// 表面积
double Area(){
double ret=0.0;
for(int i=0;i<cnt;i++){
ret+=area(P[F[i].a],P[F[i].b],P[F[i].c]);
}
return ret/2.0;
}
// 体积
double Volumn(){
point I(0,0,0);
double vv=0.0;
for(int i=0;i<cnt;i++){
vv+=volumn(I,P[F[i].a],P[F[i].b],P[F[i].c]);
}
return fabs(vv/6.0);
}
// 表面积三角形数
int tri_cnt(){
return cnt;
}
// 表面积多边形数
int fac_cnt(){
int ans=0;
for(int i=0;i<cnt;i++){
int sm=1;
for(int j=0;j<i;j++){
if(same(i,j)) {
sm=0;
break;
}
}
ans=ans+sm;
}
return ans;
}
};
ch3D Hull;
void show(point pp){
cout<<pp.x<<" "<<pp.y<<" "<<pp.z<<endl;
}
int main()
{
//freopen("cin.txt","r",stdin);
while(~scanf("%d",&Hull.n)){
for(int i=0;i<Hull.n;i++){
scanf("%lf%lf%lf",&Hull.P[i].x,&Hull.P[i].y,&Hull.P[i].z);
}
Hull.construct();
printf("%.3lf\n",Hull.Area());
}
return 0;
}
HDU 3662
3D Convex Hull
http://acm.hdu.edu.cn/showproblem.php?pid=3662
求解包含所有点的最小多面体的表面上面的个数
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-7;
const int N=5e2+10;
struct point{
double x,y,z;
point(){ x=0; y=0; z=0; }
point(double _x,double _y,double _z):x(_x),y(_y),z(_z) {}
point operator -(const point other){
return point(x-other.x,y-other.y,z-other.z);
}
point operator *(const point other){
return point(y*other.z-z*other.y,-x*other.z+z*other.x,x*other.y-y*other.x);
}
double operator ^(const point other){ //点乘
return x*other.x+y*other.y+z*other.z;
}
};
struct ch3D{
struct fac{
int a,b,c; // 面上三点的编号
bool ok; // 是否属于凸包
};
int n; //初始点数
point P[N]; //初始点
int cnt; //凸包上的三角形
fac F[N*6]; // 被创建的面不超过6N
int vis[N][N];
double vlen(point v){
return sqrt(v.x*v.x+v.y*v.y+v.z*v.z);
}
double area(point p1,point p2,point p3){
return vlen((p2-p1)*(p3-p1)); // 三角形面积*2
}
double volumn(point p1,point p2,point p3,point p4){
return fabs((p2-p1)*(p3-p1)^(p4-p1)); //V的6倍
}
double pToPlane(point p,fac ff){ // 点在面的同向: +
point m=P[ff.b]-P[ff.a];
point n=P[ff.c]-P[ff.a];
point v=p-P[ff.a];
return m*n^v;
}
void deal(int p,int a,int b){
int f=vis[a][b];
fac add;
if(F[f].ok){
if(pToPlane(P[p],F[f])>eps) dfs(p,f); //在同侧,能看见
else {
add.a=b, add.b=a, add.c=p, add.ok=1;
vis[p][b]=vis[a][p]=vis[b][a]=cnt;
F[cnt++]=add;
}
}
}
void dfs(int p,int num){ // 维护凸包
F[num].ok=0; //删除能看见的面
deal(p,F[num].b,F[num].a);
deal(p,F[num].c,F[num].b);
deal(p,F[num].a,F[num].c);
}
bool same(int s,int e){ //判断两个面是否是同一个面
point a=P[F[s].a],b=P[F[s].b],c=P[F[s].c];
return fabs(volumn(a,b,c,P[F[e].a]))<eps
&& fabs(volumn(a,b,c,P[F[e].b]))<eps
&& fabs(volumn(a,b,c,P[F[e].c]))<eps;
}
void construct(){
cnt=0;
if(n<4) return ;
/************判断四点不共面*************/
bool jud=1;
// 两点在线
for(int i=1;i<n;i++) {
if(vlen(P[0]-P[i])>eps){
jud=0;
swap(P[1],P[i]);
break;
}
}
if(jud) return ;
jud=1;
// 三点在面
for(int i=2;i<n;i++){
if(vlen((P[0]-P[1])*(P[0]-P[i]))>eps){
swap(P[2],P[i]);
jud=0;
break;
}
}
if(jud) return ;
jud=1;
// 四点成体
for(int i=3;i<n;i++){
if(volumn(P[0],P[1],P[2],P[i])>eps){
swap(P[3],P[i]);
jud=0;
break;
}
}
if(jud) return ;
/*************************************/
fac add;
for(int i=0;i<4;i++){
add.a=(i+1)%4;
add.b=(i+2)%4;
add.c=(i+3)%4;
add.ok=1;
if(pToPlane(P[i],add)>0) swap(add.b,add.c);
vis[add.a][add.b]=vis[add.b][add.c]=vis[add.c][add.a]=cnt;
F[cnt++]=add;
}
for(int i=4;i<n;i++){
for(int j=0;j<cnt;j++){
if(F[j].ok && pToPlane(P[i],F[j])>eps){
dfs(i,j);
break;
}
}
}
int tmp=cnt;
cnt=0;
for(int i=0;i<tmp;i++){
if(F[i].ok){
F[cnt++]=F[i]; // cnt speed < i speed
}
}
}
// 表面积
double Area(){
double ret=0.0;
for(int i=0;i<cnt;i++){
ret+=area(P[F[i].a],P[F[i].b],P[F[i].c]);
}
return ret/2.0;
}
// 体积
double Volumn(){
point I(0,0,0);
double vv=0.0;
for(int i=0;i<cnt;i++){
vv+=volumn(I,P[F[i].a],P[F[i].b],P[F[i].c]);
}
return fabs(vv/6.0);
}
// 表面积三角形数
int tri_cnt(){
return cnt;
}
// 表面积多边形数
int fac_cnt(){
int ans=0;
for(int i=0;i<cnt;i++){
int sm=1;
for(int j=0;j<i;j++){
if(same(i,j)) {
sm=0;
break;
}
}
ans=ans+sm;
}
return ans;
}
};
ch3D Hull;
void show(point pp){
cout<<pp.x<<" "<<pp.y<<" "<<pp.z<<endl;
}
int main()
{
//freopen("cin.txt","r",stdin);
while(~scanf("%d",&Hull.n)){
for(int i=0;i<Hull.n;i++){
scanf("%lf%lf%lf",&Hull.P[i].x,&Hull.P[i].y,&Hull.P[i].z);
}
Hull.construct();
printf("%d\n",Hull.fac_cnt());
}
return 0;
}