N皇后问题的两个最高效的算法
本文转自http://blog.csdn.net/hackbuteer1/article/details/6657109
N皇后问题是一个经典的问题,在一个N*N的棋盘上放置N个皇后,每行一个并使其不能互相攻击(同一行、同一列、同一斜线上的皇后都会自动攻击)。
一、 求解N皇后问题是算法中回溯法应用的一个经典案例
回溯算法也叫试探法,它是一种系统地搜索问题的解的方法。回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
在现实中,有很多问题往往需要我们把其所有可能穷举出来,然后从中找出满足某种要求的可能或最优的情况,从而得到整个问题的解。回溯算法就是解决这种问题的“通用算法”,有“万能算法”之称。N皇后问题在N增大时就是这样一个解空间很大的问题,所以比较适合用这种方法求解。这也是N皇后问题的传统解法,很经典。
下面是算法的高级伪码描述,这里用一个N*N的矩阵来存储棋盘:
1) 算法开始, 清空棋盘,当前行设为第一行,当前列设为第一列
2) 在当前行,当前列的位置上判断是否满足条件(即保证经过这一点的行,列与斜线上都没有两个皇后),若不满足,跳到第4步
3) 在当前位置上满足条件的情形:
在当前位置放一个皇后,若当前行是最后一行,记录一个解;
若当前行不是最后一行,当前行设为下一行, 当前列设为当前行的第一个待测位置;
若当前行是最后一行,当前列不是最后一列,当前列设为下一列;
若当前行是最后一行,当前列是最后一列,回溯,即清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置;
以上返回到第2步
4) 在当前位置上不满足条件的情形:
若当前列不是最后一列,当前列设为下一列,返回到第2步;
若当前列是最后一列了,回溯,即,若当前行已经是第一行了,算法退出,否则,清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置,返回到第2步;
算法的基本原理是上面这个样子,但不同的是用的数据结构不同,检查某个位置是否满足条件的方法也不同。为了提高效率,有各种优化策略,如多线程,多分配内存表示棋盘等。
在具体解决该问题时,可以将其拆分为几个小问题。首先就是在棋盘上如何判断两个皇后是否能够相互攻击,在最初接触这个问题时,首先想到的方法就是把棋盘存储为一个二维数组,然后在需要在第i行第j列放置皇后时,根据问题的描述,首先判断是在第i行是否有皇后,由于每行只有一个皇后,这个判断也可以省略,然后判断第j列是否有皇后,这个也很简单,最后需要判断在同一斜线上是否有皇后,按照该方法需要判断两次,正对角线方向和负对角线方向,总体来说也不难。但是写完之后,总感觉很笨,因为在N皇后问题中这个函数的使用次数太多了,而这样做效率较差,个人感觉很不爽。上网查看了别人的实现之后大吃一惊,大牛们都是使用一个一维数组来存储棋盘,在某个位置上是否有皇后可以相互攻击的判断也很简单。具体细节如下:
把棋盘存储为一个N维数组a[N],数组中第i个元素的值代表第i行的皇后位置,这样便可以把问题的空间规模压缩为一维O(N),在判断是否冲突时也很简单,首先每行只有一个皇后,且在数组中只占据一个元素的位置,行冲突就不存在了,其次是列冲突,判断一下是否有a[i]与当前要放置皇后的列j相等即可。至于斜线冲突,通过观察可以发现所有在斜线上冲突的皇后的位置都有规律即它们所在的行列互减的绝对值相等,即| row – i | = | col – a[i] | 。这样某个位置是否可以放置皇后的问题已经解决。
下面要解决的是使用何种方法来找到所有的N皇后的解。上面说过该问题是回溯法的经典应用,所以可以使用回溯法来解决该问题,具体实现也有两个途径,递归和非递归。递归方法较为简单,大致思想如下:
void queen(int row)
{
if (n == row) //如果已经找到结果,则打印结果
print_result();
else {
for (k=0 to N) { //试探第row行每一个列
if (can_place(row, k) {
place(row, k); //放置皇后
queen(row + 1); //继续探测下一行
}
}
}
}
该方法由于在探测第i行后,如果找到一个可以放置皇后的位置j后,则会递归探测下一行,结束后则会继续探测i行j+1列,故可以找到所有的N皇后的解。
但是一般来说递归的效率比较差,下面重点讨论一下该问题的非递归实现。
非递归方法的一个重要问题时何时回溯及如何回溯的问题。程序首先对N行中的每一行进行探测,寻找该行中可以放置皇后的位置,具体方法是对该行的每一列进行探测,看是否可以放置皇后,如果可以,则在该列放置一个皇后,然后继续探测下一行的皇后位置。如果已经探测完所有的列都没有找到可以放置皇后的列,此时就应该回溯,把上一行皇后的位置往后移一列,如果上一行皇后移动后也找不到位置,则继续回溯直至某一行找到皇后的位置或回溯到第一行,如果第一行皇后也无法找到可以放置皇后的位置,则说明已经找到所有的解程序终止。如果该行已经是最后一行,则探测完该行后,如果找到放置皇后的位置,则说明找到一个结果,打印出来。但是此时并不能再此处结束程序,因为我们要找的是所有N皇后问题所有的解,此时应该清除该行的皇后,从当前放置皇后列数的下一列继续探测。
完整的代码如下:
/**
* 回溯法解N皇后问题
* 使用一个一维数组表示皇后的位置
* 其中数组的下标表示皇后所在的行
* 数组元素的值表示皇后所在的列
* 这样设计的棋盘,所有皇后必定不在同一行,于是行冲突就不存在了
* date : 2011-08-03
* author: liuzhiwei
**/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define QUEEN 8 //皇后的数目
#define INITIAL -10000 //棋盘的初始值
int a[QUEEN]; //一维数组表示棋盘
void init() //对棋盘进行初始化
{
int *p;
for (p = a; p < a + QUEEN; ++p)
{
*p = INITIAL;
}
}
int valid(int row, int col) //判断第row行第col列是否可以放置皇后
{
int i;
for (i = 0; i < QUEEN; ++i) //对棋盘进行扫描
{
if (a[i] == col || abs(i - row) == abs(a[i] - col)) //判断列冲突与斜线上的冲突
return 0;
}
return 1;
}
void print() //打印输出N皇后的一组解
{
int i, j;
for (i = 0; i < QUEEN; ++i)
{
for (j = 0; j < QUEEN; ++j)
{
if (a[i] != j) //a[i]为初始值
printf("%c ", '.');
else //a[i]表示在第i行的第a[i]列可以放置皇后
printf("%c ", '#');
}
printf("\n");
}
for (i = 0; i < QUEEN; ++i)
printf("%d ", a[i]);
printf("\n");
printf("--------------------------------\n");
}
void queen() //N皇后程序
{
int n = 0;
int i = 0, j = 0;
while (i < QUEEN)
{
while (j < QUEEN) //对i行的每一列进行探测,看是否可以放置皇后
{
if(valid(i, j)) //该位置可以放置皇后
{
a[i] = j; //第i行放置皇后
j = 0; //第i行放置皇后以后,需要继续探测下一行的皇后位置,所以此处将j清零,从下一行的第0列开始逐列探测
break;
}
else
{
++j; //继续探测下一列
}
}
if(a[i] == INITIAL) //第i行没有找到可以放置皇后的位置
{
if (i == 0) //回溯到第一行,仍然无法找到可以放置皇后的位置,则说明已经找到所有的解,程序终止
break;
else //没有找到可以放置皇后的列,此时就应该回溯
{
--i;
j = a[i] + 1; //把上一行皇后的位置往后移一列
a[i] = INITIAL; //把上一行皇后的位置清除,重新探测
continue;
}
}
if (i == QUEEN - 1) //最后一行找到了一个皇后位置,说明找到一个结果,打印出来
{
printf("answer %d : \n", ++n);
print();
//不能在此处结束程序,因为我们要找的是N皇后问题的所有解,此时应该清除该行的皇后,从当前放置皇后列数的下一列继续探测。
//_sleep(600);
j = a[i] + 1; //从最后一行放置皇后列数的下一列继续探测
a[i] = INITIAL; //清除最后一行的皇后位置
continue;
}
++i; //继续探测下一行的皇后位置
}
}
int main(void)
{
init();
queen();
system("pause");
return 0;
}
下面的代码跟上面的代码差不多,只是稍微做了一些变化。。上面函数判断棋盘某个位置合法性的时候,valid函数里面的QUEEN可以修改为row的,只需要将前面row行与第row行进行比较就可以了,不需要将所有行都与第row进行比较的。。。下面的代码中的check函数中循环次数是k而不是皇后的个数就是这个原因。。。
#include "iostream"
#include "cmath"
using namespace std;
#define Max 20 //定义棋盘的最大值
int a[Max];
int show(int S) //定义输出函数
{
int i,p,q;
int b[Max][Max]={0}; //定义并初始化b[][]输出数组
for(i=1;i<=S;i++) //按横列i顺序输出a[i]数组坐标
{
b[i][a[i]]=1;
printf("(%d,%d)\t",i,a[i]);
}
printf("\n");
for(p=1;p<=S;p++) //按棋盘的横列p顺序标明皇后的位置
{
for(q=1;q<=S;q++)
{
if(b[p][q]==1) //在第p行第q列放置一个皇后棋子
printf("●");
else
printf("○");
}
printf("\n");
}
return 0;
}
int check(int k) //定义check函数
{
int i;
for(i=1;i<k;i++) //将第k行与前面的第1~~k-1行进行判断
{
if((a[i]==a[k]) || (a[i]-a[k]==k-i) || (a[i]-a[k]==i-k)) //检查是否有多个皇后在同一条直线上
{
return 0;
}
}
return 1;
}
void check_m(int num) //定义函数
{
int k=1,count=0;
printf("The possible configuration of N queens are:\n");
a[k]=1;
while(k>0)
{
if(k<=num && a[k]<=num) //从第k行第一列的位置开始,为后续棋子选择合适位子
{
if(check(k)==0) //第k行的a[k]列不能放置皇后
{
a[k]++; //继续探测当前行的下一列:a[k]+1
}
else
{
k++; //第K行的位置已经确定了,继续寻找第k+1行皇后的位置
a[k]=1; //从第一列开始查找
}
}
else
{
if(k>num) //若满足输出数组的要求则输出该数组
{
count++;
printf("[%d]: ",count);
show(num); //调用输出函数show()
}
//如果k>num会执行下面两行代码,因为虽然找到了N皇后问题的一个解,但是要找的是所有解,需要回溯,从当前放置皇后的下一列继续探测
//如果a[k]>num也会执行下面两行代码,就是说在当前行没有找到可以放置皇后的位置,于是回溯,从上一行皇后位置的下一列继续探测
k--; //棋子位置不符合要求,则退回前一步
a[k]++; //继续试探下一列位置
}
}
printf("The count is: %d \n",count);
}
int main(void)
{
int N,d;
//system("color 2a");
do
{
printf("********************N皇后问题系统*********************\n\n");
printf(" 1. 四皇后问题 \n");
printf(" 2. 八皇后问题 \n");
printf(" 3. N 皇后问题(N<20) \n");
printf(" 4. 退出 \n");
printf("******************************************************\n");
printf("\n 从数字1-4之间的数选择需要的操作\n\n"); /*提示输入选项*/
printf(" 请输入你要选择的功能选项:__\n");
scanf("%d",&d);
switch(d)
{
case 1:
check_m(4); //4皇后问题
break;
case 2:
check_m(8); //8皇后问题
break;
case 3:
printf("请输入N的值:_");
fflush(stdin); //清除缓冲
scanf("%d",&N);
printf("\n");
if(N>0&&N<20)
{
check_m(N); //N皇后问题
break;
}
else
{
printf("输入错误,请从新输入:");
printf("\n\n");
break;
}
case 4:
exit(0); //程序结束
}
}while(1);
system("pause");
return 0;
}
递归解法:
#include <stdio.h>
#include <stdlib.h>
const int N=20; //最多放皇后的个数
int q[N]; //各皇后所在的行号
int cont = 0; //统计解得个数
//输出一个解
void print(int n)
{
int i,j;
cont++;
printf("第%d个解:",cont);
for(i=1;i<=n;i++)
printf("(%d,%d) ",i,q[i]);
printf("\n");
for(i=1;i<=n;i++) //行
{
for(j=1;j<=n;j++) //列
{
if(q[i]!=j)
printf("x ");
else
printf("Q ");
}
printf("\n");
}
}
//检验第i行的k列上是否可以摆放皇后
int find(int i,int k)
{
int j=1;
while(j<i) //j=1~i-1是已经放置了皇后的行
{
//第j行的皇后是否在k列或(j,q[j])与(i,k)是否在斜线上
if(q[j]==k || abs(j-i)==abs(q[j]-k))
return 0;
j++;
}
return 1;
}
//放置皇后到棋盘上
void place(int k,int n)
{
int j;
if(k>n)
print(n);
else
{
for(j=1;j<=n;j++) //试探第k行的每一个列
{
if(find(k,j))
{
q[k] = j;
place(k+1,n); //递归总是在成功完成了上次的任务的时候才做下一个任务
}
}
}
}
int main(void)
{
int n;
printf("请输入皇后的个数(n<=20),n=:");
scanf("%d",&n);
if(n>20)
printf("n值太大,不能求解!\n");
else
{
printf("%d皇后问题求解如下(每列的皇后所在的行数):\n",n);
place(1,n); //问题从最初状态解起
printf("\n");
}
system("pause");
return 0;
}
二、使用位运算来求解N皇后的高效算法
核心代码如下:
void test(int row, int ld, int rd)
{
int pos, p;
if ( row != upperlim )
{
pos = upperlim & (~(row | ld | rd ));
while ( pos )
{
p = pos & (~pos + 1);
pos = pos - p;
test(row | p, (ld | p) << 1, (rd | p) >> 1);
}
}
else
++Ans;
}
初始化: upperlim = (1 << n)-1; Ans = 0;
调用参数:test(0, 0, 0);
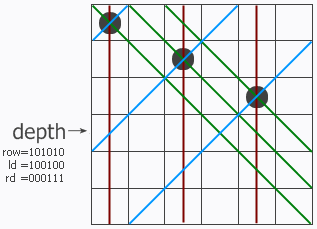
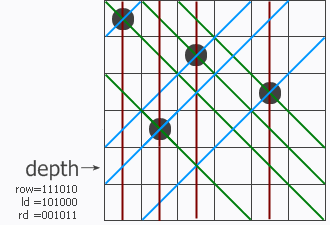
和普通算法一样,这是一个递归函数,程序一行一行地寻找可以放皇后的地方。函数带三个参数row、ld和rd,分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方不能放。位于该行上的冲突位置就用row、ld和rd中的1来表示。把它们三个并起来,得到该行所有的禁位,取反后就得到所有可以放的位置(用pos来表示)。
p = pos & (~pos + 1)其结果是取出最右边的那个1。这样,p就表示该行的某个可以放子的位置,把它从pos中移除并递归调用test过程。
注意递归调用时三个参数的变化,每个参数都加上了一个禁位,但两个对角线方向的禁位对下一行的影响需要平移一位。最后,如果递归到某个时候发现row=upperlim了,说明n个皇后全放进去了,找到的解的个数加一。
注:
upperlime:=(1 << n)-1 就生成了n个1组成的二进制数。
这个程序是从上向下搜索的。
pos & -pos 的意思就是取最右边的 1 再组成二进制数,相当于 pos &(~pos +1),因为取反以后刚好所有数都是相反的(怎么听着像废话),再加 1 ,就是改变最低位,如果低位的几个数都是1,加的这个 1 就会进上去,一直进到 0 ,在做与运算就和原数对应的 1 重合了。举例可以说明:
原数 0 0 0 0 1 0 0 0 原数 0 1 0 1 0 0 1 1
取反 1 1 1 1 0 1 1 1 取反 1 0 1 0 1 1 0 0
加1 1 1 1 1 1 0 0 0 加1 1 0 1 0 1 1 0 1
与运算 0 0 0 0 1 0 0 0 and 0 0 0 0 0 0 0 1
其中呢,这个取反再加 1 就是补码,and 运算 与负数,就是按位和补码与运算。
(ld | p)<< 1 是因为由ld造成的占位在下一行要右移一下;
(rd | p)>> 1 是因为由rd造成的占位在下一行要左移一下。
ld rd row 还要和upperlime 与运算 一下,这样做的结果就是从最低位数起取n个数为有效位置,原因是在上一次的运算中ld发生了右移,如果不and的话,就会误把n以外的位置当做有效位。
pos 已经完成任务了还要减去p 是因为?
while 循环是因为?
在进行到某一层的搜索时,pos中存储了所有的可放位置,为了求出所有解,必须遍历所有可放的位置,而每走过一个点必须要删掉它,否则就成死循环啦!
这个是目前公认N皇后的最高效算法。
完整的代码如下:
/*
** 目前最快的N皇后递归解决方法
** N Queens Problem
** 试探-回溯算法,递归实现
*/
#include "iostream"
using namespace std;
#include "time.h"
// sum用来记录皇后放置成功的不同布局数;upperlim用来标记所有列都已经放置好了皇后。
long sum = 0, upperlim = 1;
// 试探算法从最右边的列开始。
void test(long row, long ld, long rd)
{
if (row != upperlim)
{
// row,ld,rd进行“或”运算,求得所有可以放置皇后的列,对应位为0,
// 然后再取反后“与”上全1的数,来求得当前所有可以放置皇后的位置,对应列改为1
// 也就是求取当前哪些列可以放置皇后
long pos = upperlim & ~(row | ld | rd);
while (pos) // 0 -- 皇后没有地方可放,回溯
{
// 拷贝pos最右边为1的bit,其余bit置0
// 也就是取得可以放皇后的最右边的列
long p = pos & -pos;
// 将pos最右边为1的bit清零
// 也就是为获取下一次的最右可用列使用做准备,
// 程序将来会回溯到这个位置继续试探
pos -= p;
// row + p,将当前列置1,表示记录这次皇后放置的列。
// (ld + p) << 1,标记当前皇后左边相邻的列不允许下一个皇后放置。
// (ld + p) >> 1,标记当前皇后右边相邻的列不允许下一个皇后放置。
// 此处的移位操作实际上是记录对角线上的限制,只是因为问题都化归
// 到一行网格上来解决,所以表示为列的限制就可以了。显然,随着移位
// 在每次选择列之前进行,原来N×N网格中某个已放置的皇后针对其对角线
// 上产生的限制都被记录下来了
test(row + p, (ld + p) << 1, (rd + p) >> 1);
}
}
else
{
// row的所有位都为1,即找到了一个成功的布局,回溯
sum++;
}
}
int main(int argc, char *argv[])
{
time_t tm;
int n = 16;
if (argc != 1)
n = atoi(argv[1]);
tm = time(0);
// 因为整型数的限制,最大只能32位,
// 如果想处理N大于32的皇后问题,需要
// 用bitset数据结构进行存储
if ((n < 1) || (n > 32))
{
printf(" 只能计算1-32之间\n");
exit(-1);
}
printf("%d 皇后\n", n);
// N个皇后只需N位存储,N列中某列有皇后则对应bit置1。
upperlim = (upperlim << n) - 1;
test(0, 0, 0);
printf("共有%ld种排列, 计算时间%d秒 \n", sum, (int) (time(0) - tm));
system("pause");
return 0;
}
上述代码还是比较容易看懂的,但我觉得核心的是在针对试探-回溯算法所用的数据结构的设计上。
程序采用了递归,也就是借用了编译系统提供的自动回溯功能。
算法的核心:使用bit数组来代替以前由int或者bool数组来存储当前格子被占用或者说可用信息,从这可以看出N个皇后对应需要N位表示。
巧妙之处在于:以前我们需要在一个N*N正方形的网格中挪动皇后来进行试探回溯,每走一步都要观察和记录一个格子前后左右对角线上格子的信息;采用bit位进行信息存储的话,就可以只在一行格子也就是(1行×N列)个格子中进行试探回溯即可,对角线上的限制被化归为列上的限制。
程序中主要需要下面三个bit数组,每位对应网格的一列,在C中就是取一个整形数的某部分连续位即可。 row用来记录当前哪些列上的位置不可用,也就是哪些列被皇后占用,对应为1。ld,rd同样也是记录当前哪些列位置不可用,但是不表示被皇后占用,而是表示会被已有皇后在对角线上吃掉的位置。这三个位数组进行“或”操作后就是表示当前还有哪些位置可以放置新的皇后,对应0的位置可放新的皇后。如下图所示的8皇后问题求解得第一步:
row: [ ][ ][ ][ ][ ][ ][ ][*]
ld: [ ][ ][ ][ ][ ][ ][*][ ]
rd: [ ][ ][ ][ ][ ][ ][ ][ ]
--------------------------------------
row|ld|rd: [ ][ ][ ][ ][ ][ ][*][*]
所有下一个位置的试探过程都是通过位操作来实现的,这是借用了C语言的好处,详见代码注释。
关于此算法,如果考虑N×N棋盘的对称性,对于大N来说仍能较大地提升效率!
位操作--对优化算法有了个新的认识
这个是在csdn找到的一个N皇后问题最快的算法,看了好一会才明白,这算法巧妙之处我认为有2个:
1、以前都是用数组来描述状态,而这算法采用是的位来描述,运算速度可以大大提升,以后写程序对于描述状态的变量大家可以借鉴这个例子,会让你的程序跑得更快
2、描述每行可放置的位置都是只用row,ld,rd这3个变量来描述,这样使得程序看起来挺简洁的。