【Codeforces Round 340 (Div 2)D】【讨论题】Polyline 三点用最少数量连续不分叉线段连接

D. Polyline

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There are three points marked on the coordinate plane. The goal is to make a simple polyline, without self-intersections and self-touches, such that it passes through all these points. Also, the polyline must consist of only segments parallel to the coordinate axes. You are to find the minimum number of segments this polyline may consist of.

Input

Each of the three lines of the input contains two integers. The i-th line contains integers x_i and y_i( - 10⁹ ≤ x_i, y_i ≤ 10⁹) — the coordinates of the i-th point. It is guaranteed that all points are distinct.

Output

Print a single number — the minimum possible number of segments of the polyline.

Examples

input

1 -1
1 1
1 2

output

1

input

-1 -1
-1 3
4 3

output

2

input

1 1
2 3
3 2

output

3

Note

The variant of the polyline in the first sample: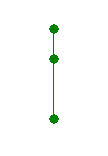The variant of the polyline in the second sample: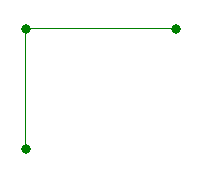The variant of the polyline in the third sample:

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 0, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n;
int x[3], y[3];
int main()
{
	while (~scanf("%d%d",&x[0],&y[0]))
	{
		for (int i = 1; i < 3; ++i)scanf("%d%d", &x[i], &y[i]);
		int sam = 0;
		for (int i = 0; i < 3; ++i)
		{
			int X = 0;
			int Y = 0;
			for (int j = 0; j < 3; ++j)
			{
				if (x[j] == x[i])++X;
				if (y[j] == y[i])++Y;
			}
			gmax(sam, X);
			gmax(sam, Y);
		}
		if (sam == 3)puts("1");
		else if (sam == 2)
		{
			bool flag = 0;
			for (int i = 0; i < 3; ++i)
			{
				for (int j = 0; j < 3; ++j)if (j != i)
				{
					int k = 3 - i - j;
					if (x[i] == x[j])
					{
						if (y[k]<=min(y[i], y[j]) || y[k]>=max(y[i], y[j]))flag = 1;
					}
					if (y[i] == y[j])
					{
						if (x[k]<=min(x[i], x[j]) || x[k]>=max(x[i], x[j]))flag = 1;
					}
				}
			}
			if (flag)puts("2");
			else puts("3");
		}
		else puts("3");
	}
	return 0;
}
/*
【trick&&吐槽】
细节啊，<= >=被我写成了< 和 >，肯定要错啊
新添啊，稳住，保证正确率是关键。连样例都不过我竟然就交了。。。

【题意】
有3个点，给你每个点的坐标。
问你，我们至少要画几条连续的线段（不可分叉），使得3个点都在线段上。

【类型】
讨论

【分析】
这题只要小小地讨论一下就可以AC啦。

1，三点共线：1
2，任意两点横纵坐标都不相同：3
3，两点共线，且第三点在这条线段"内"（比如0 0，0 10，5 5）：3
4，两点共线，且第三点在这条线段"外"（比如0 0，0 10，5 15）：2

【时间复杂度&&优化】
O（n）

*/