【Codeforces Round 269 (Div 2)D】【KMP】我们的积木和目标积木的等增幅的匹配位点数
Polar bears Menshykov and Uslada from the zoo of St. Petersburg and elephant Horace from the zoo of Kiev got hold of lots of wooden cubes somewhere. They started making cube towers by placing the cubes one on top of the other. They defined multiple towers standing in a line as a wall. A wall can consist of towers of different heights.
Horace was the first to finish making his wall. He called his wall an elephant. The wall consists of w towers. The bears also finished making their wall but they didn't give it a name. Their wall consists of n towers. Horace looked at the bears' tower and wondered: in how many parts of the wall can he "see an elephant"? He can "see an elephant" on a segment of w contiguous towers if the heights of the towers on the segment match as a sequence the heights of the towers in Horace's wall. In order to see as many elephants as possible, Horace can raise and lower his wall. He even can lower the wall below the ground level (see the pictures to the samples for clarification).
Your task is to count the number of segments where Horace can "see an elephant".
The first line contains two integers n and w (1 ≤ n, w ≤ 2·105) — the number of towers in the bears' and the elephant's walls correspondingly. The second line contains n integers ai (1 ≤ ai ≤ 109) — the heights of the towers in the bears' wall. The third line contains w integers bi (1 ≤ bi ≤ 109) — the heights of the towers in the elephant's wall.
Print the number of segments in the bears' wall where Horace can "see an elephant".
13 5 2 4 5 5 4 3 2 2 2 3 3 2 1 3 4 4 3 2
2
The picture to the left shows Horace's wall from the sample, the picture to the right shows the bears' wall. The segments where Horace can "see an elephant" are in gray.
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre(){freopen("c://test//input.in","r",stdin);freopen("c://test//output.out","w",stdout);}
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1,class T2>inline void gmax(T1 &a,T2 b){if(b>a)a=b;}
template <class T1,class T2>inline void gmin(T1 &a,T2 b){if(b<a)a=b;}
const int N=2e5+10,M=0,Z=1e9+7,ms63=1061109567;
int n,m;
int w[N],a[N],b[N];
int nxt[N];
void getnxt()
{
int j=0;nxt[1]=0;
for(int i=2;i<=m;++i)
{
while(j&&b[j+1]!=b[i])j=nxt[j];
if(b[j+1]==b[i])++j;
nxt[i]=j;
}
}
void kmp()
{
int ans=0;
int j=0;
for(int i=1;i<=n;++i)
{
while(j&&b[j+1]!=a[i])j=nxt[j];
if(b[j+1]==a[i])++j;
if(j==m)++ans;
}
printf("%d\n",ans);
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
for(int i=1;i<=n;++i)scanf("%d",&w[i]);
for(int i=1;i<n;++i)a[i]=w[i]-w[i+1];//a[n]=-2e9;--n;
for(int i=1;i<=m;++i)scanf("%d",&w[i]);
for(int i=1;i<m;++i)b[i]=w[i]-w[i+1];//b[m]=-2e9;--m;
if(m==0)
{
printf("%d\n",n+1);
continue;
}
getnxt();
kmp();
}
return 0;
}
/*
【trick&&吐槽】
1，一定要特判m==1的情况，这个时候我们做KMP的匹配位点最多也不过n-1个。而事实上答案是n。
2，本来在KMP中是利用s[strlen(s)]==0，来自然实现匹配封堵。
然而数组中没有这个自然封堵，所以我们用不会出现的数值封堵下，以避免超长度匹配的错误情况。
【题意】
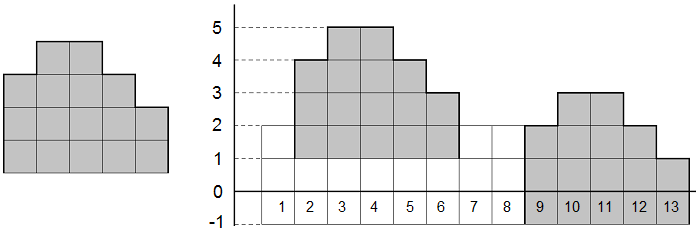
给你一个长度为n（1<=n<=2e5）的一排积木，长度分别为a[]（1<=a[]<=1e9）。
有一个长度为m（1<=m<=2e5）的一排积木，长度分别为b[]（1<=b[]<=1e9）
问你，第一排积木有多少个位点i，使得[i+0,i+m-1]这一段积木，之间增减幅度与b[]的整体增减幅度相同。
【类型】
KMP
【分析】
增减幅度肯定产生于相邻的积木之间。
于是我们求出第二排积木之间的m-1个增减幅度。
然后求出第一排积木之间的n-1个增减幅度。
然后以第二个串作为模板串，第一个串为匹配串。
做KMP匹配求匹配位点个数，就是答案啦！
【时间复杂度&&优化】
O（n+m）
【数据】
不封堵的话——
input
3 2
0 0 0
0 0
output
1（实际答案是2。但是匹配长度变长了，m==2的变得>2了，答案就会变小）
*/