基于堆积树的选择排序（Heap排序法）

Heap排序法算法分析

选择排序法的概念简单，每次从未排序部份选一最小值，插入已排序部份的后端，其时间主要花费于在整个未排序部份寻找最小值，如果能让搜寻最小值的方式加 快，选择排序法的速率也就可以加快，Heap排序法让搜寻的路径由树根至最后一个树叶，而不是整个未排序部份，因而称之为改良的选择排序法。

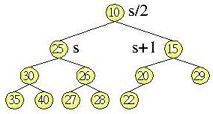
Heap排序法使用Heap Tree（堆积树），树是一种资料结构，而堆积树是一个二元树，也就是每一个父节点最多只有两个子节点（关于树的详细定义还请见资料结构书籍），堆积树的 父节点若小于子节点，则称之为最小堆积（Min Heap），父节点若大于子节点，则称之为最大堆积（Max Heap），而同一层的子节点则无需理会其大小关系，例如下面就是一个堆积树： 

可以使用一维阵列来储存堆积树的所有元素与其顺序，为了计算方便，使用的起始索引是1而不是0，索引1是树根位置，如果左子节点储存在阵列中的索引为s，则其父节点的索引为s/2，而右子节点为s+1，就如上图所示，将上图的堆积树转换为一维阵列之后如下所示：

首先必须知道如何建立堆积树，加至堆积树的元素会先放置在最后一个树叶节点位置，然后检查父节点是否小于子节点（最小堆积），将小的元素不断与父节点交换，直到满足堆积树的条件为止，例如在上图的堆积加入一个元素12，则堆积树的调整方式如下所示：

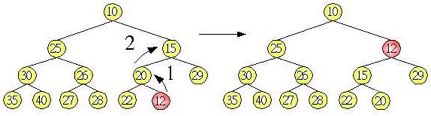
建立好堆积树之后，树根一定是所有元素的最小值，您的目的就是：

将最小值取出

然后调整树为堆积树

 

不断重复以上的步骤，就可以达到排序的效果，最小值的取出方式是将树根与最后一个树叶节点交换，然后切下树叶节点，重新调整树为堆积树，如下所示：

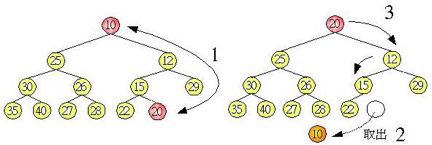
调整完毕后，树根节点又是最小值了，于是我们可以重覆这个步骤，再取出最小值，并调整树为堆积树，如下所示：

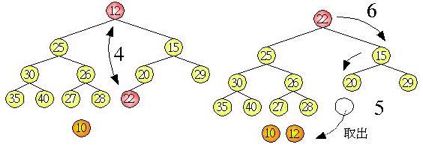
如此重覆步骤之后，由于使用一维阵列来储存堆积树，每一次将树叶与树根交换的动作就是将最小值放至后端的阵列，所以最后阵列就是变为已排序的状态。

其实堆积在调整的过程中，就是一个选择的行为，每次将最小值选至树根，而选择的路径并不是所有的元素，而是由树根至树叶的路径，因而可以加快选择的过程， 所以Heap排序法才会被称之为改良的选择排序法。

代码实现（C/OC）

#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;}

void createheap(int[]);
void heapsortt(int[]);

//主程序（C/OC）
int number[MAX+1] = {-1};
int i, num;

srand(time(NULL));

printf("排序前：");
for(i = 1; i <= MAX; i++) {     //生成排序前的数组
    number[i] = rand() % 100;
    printf("%d ", number[i]);
}

printf("\n建立堆积树：");
createheap(number);             //建立堆积树
for(i = 1; i <= MAX; i++)       //打印堆积树
    printf("%d ", number[i]);
printf("\n");

heapsortt(number);              //利用堆积树进行选择排序
printf("\n");

//建立堆积树
void createheap(int number[]) {     
    int i, s, p;
    int heap[MAX+1] = {-1};         //临时数组
    
    for(i = 1; i <= MAX; i++) {     //依次排列堆积树中的每个元素的值，i为多少，就排第几个
        heap[i] = number[i];
        s = i;
        p = i / 2;                  //除以2，正好可以获得父节点的下标
        while(s >= 2 && heap[p] > heap[s]) {//如果父节点大于子节点的值，交换
            SWAP(heap[p], heap[s]);
            s = p;
            p = s / 2;
        }
    }
    
    for(i = 1; i <= MAX; i++)       //赋值
        number[i] = heap[i];
}

//选择排序
void heapsortt(int number[]) {      
    int i, m, p, s;
    
    m = MAX;
    while(m > 1) {
        SWAP(number[1], number[m]);         //交换堆积树的首尾节点的值
        m--;
        
        p = 1;                              //父节点以顶点开始
        s = 2 * p;                          //指向左子节点
        
        while(s <= m) {
            if(s < m && number[s+1] < number[s])//两个子节点进行比较，右子节点较小，s指向两个中最小的子节点
                s++;
            if(number[p] <= number[s])          //父节点更小，而且因为之前为最小堆积树，所以跳出
                break;
            SWAP(number[p], number[s]);         //没有跳出，交换较小子节点与父节点
            p = s;                              //p指向新的父节点
            s = 2 * p;                          //s指向新的子节点
        }
        
        printf("\n排序中：");
        for(i = MAX; i > 0; i--)                //最小值已经放到较大下标处（已在堆积树外），故倒序打印
            printf("%d ", number[i]);
    } 
}