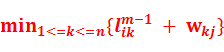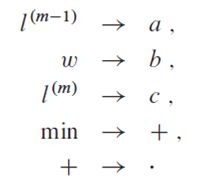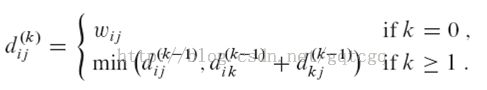算法导论笔记:25所有节点对的最短路径问题
本章考虑在给定的有向加权图G=(V, E),对于所有的节点u,v∈V,找到一条从节点u到节点v的最短路径。希望以表格的形式表示输出:第u行第v列给出的是节点u到节点v的最短路径权重。
对于这个问题,如果是运行|V|次单源最短路径算法来解决所有节点对的最短路径问题,每一次使用一个不同的节点做为源节点。如果所有边的权值是非负的,可以采用Dijkstra算法。如果采用数组来实现最小优先队列,算法的运行时间为O()=O()。使用二叉堆实现的最小优先队列将使算法的运行时间降低到O(VE lg V),这个时间在稀疏图的情况下有很大改进,因为稀疏图E <![]() 。如果采用斐波那契堆来实现最小优先队列,其算法运行时间为O(
。如果采用斐波那契堆来实现最小优先队列,其算法运行时间为O(![]() )。
)。
如果图中有权重为负值的边,就必须采用效率更低的Bellman-Ford算法,这样的运行时间将使O(![]() ),在稠密图的情况下,该运行时间为O(
),在稠密图的情况下,该运行时间为O(![]() )。
)。
本章研究的算法将能做到更好,同时,本章还讨论所有节点对最短路径问题与矩阵乘法之间的关系。
本章的多数算法采用邻接矩阵表示图,假定节点的编号为1,2,...,|V|,因此,算法的输入是n*n的矩阵W,该矩阵代表一个有n个节点的有向图的边的权重:
算法的输出也是一个n*n的矩阵D = ()。其中 = δ(i, j)。
为了解决所有顶点间最短路径问题,不仅要算出最短路径的权值,而且要计算出一个前驱节点矩阵![]() ,其中
,其中![]() 在i=j或从i到j没有通路时为NIL,其他情况下表示从i到j的某条最短路径上j的前驱顶点。由
在i=j或从i到j没有通路时为NIL,其他情况下表示从i到j的某条最短路径上j的前驱顶点。由![]() 矩阵的第i行导出的子图应是根节点为i的一棵最短路径树。下面的算法将打印出从节点i到节点j的一条最短路径,该算法类似于22章的PRINT-PATH过程:
矩阵的第i行导出的子图应是根节点为i的一棵最短路径树。下面的算法将打印出从节点i到节点j的一条最短路径,该算法类似于22章的PRINT-PATH过程:
PRINT-ALL-PAIRS-SHORTEST-PATH(![]() , i, j)
, i, j)
if i == j
print i
else if ![]() == NIL
== NIL
print “no path from i to j exists”
else PRINT-ALL-PAIRS-SHORTEST-PATH(![]() , i,
, i, ![]() )
)
print j
本章使用大写字母表示矩阵,如W, L或D,使用带下标的小写字母表示矩阵中的个体元素,如![]() 、
、![]() 或。
或。
一:最短路径和矩阵乘法
本节讨论一种动态规划算法,动态规划算法的步骤是:分析最优解的结构,递归定义最优解的值,自底向上计算最优解的值。
之前讨论单源最短路径问题时,已经证明一条最短路径的所有子路径都是最短路径。考虑从i到j的一条最短路径p,假定p最多包含m条边,假定没有权值为负值的环路,且m为有限值。如果i=j,则p的权重为0且不包含任何边。如果i和j不同,则将p分解为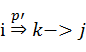 ,其中路径p’最多包含m-1条边,所以δ(i, j) =δ(i, k)+
,其中路径p’最多包含m-1条边,所以δ(i, j) =δ(i, k)+![]() 。
。
设![]() 为从i到j的最多包含m条边的任意路径中的最小权重。当m=0时,从i到j之间存在一条没有边的最短路径当且仅当i=j。所以:
为从i到j的最多包含m条边的任意路径中的最小权重。当m=0时,从i到j之间存在一条没有边的最短路径当且仅当i=j。所以:
如果i到j之间最短路径,则该路径为简单路径,其中包含的边最多为n-1,所以有:![]()
对于所有的节点i和j,有![]() = (),所以, = W。下面的算法假定已经知道了W和
= (),所以, = W。下面的算法假定已经知道了W和![]() 的情况下,给出如何计算
的情况下,给出如何计算![]() ,其中,L表示, L’表示
,其中,L表示, L’表示![]() ,该算法的时间复杂度为O():
,该算法的时间复杂度为O():
现在可以看到上面的算法与矩阵乘法的关系了。假定希望计算矩阵乘积C = A*B,对于i,j=1,2,...,n,有 = 。如果在![]() =
=  做出下面的替换:
做出下面的替换:
就可以得到 =![]() 。因此,如果对算法EXTEND-SHORTEST-PATHS做出上面的替换,就可以得到标准的矩阵乘法的算法。
。因此,如果对算法EXTEND-SHORTEST-PATHS做出上面的替换,就可以得到标准的矩阵乘法的算法。
如前所述,矩阵![]() 包含的是最短路径权重,所以,下面的算法可以在O(
包含的是最短路径权重,所以,下面的算法可以在O(![]() )时间内,计算出该矩阵阵列:
)时间内,计算出该矩阵阵列:
我们的目标并不是要计算所有的![]() 矩阵,我们感兴趣的仅仅是矩阵
矩阵,我们感兴趣的仅仅是矩阵![]() 。因为有:
。因为有:![]() 正如传统的矩阵乘法是相关的,所以由EXTEND-SHORTEST-PATHS过程所定义的算法也是相关的。所以可以采用重复平方的技术计算该矩阵序列,该算法的时间复杂度可以减少为O(
正如传统的矩阵乘法是相关的,所以由EXTEND-SHORTEST-PATHS过程所定义的算法也是相关的。所以可以采用重复平方的技术计算该矩阵序列,该算法的时间复杂度可以减少为O(![]() );
);
二:Floyd-Warshall算法
Floyd-Warshall算法采用不同的动态规划公式解决所有节点对的最短路径问题,它的运行时间是O(![]() ),该算法同样假设:可以存在负权重的边,但不能存在权重为负值的环路。
),该算法同样假设:可以存在负权重的边,但不能存在权重为负值的环路。
Floyd-Warshall算法考虑一条最短路径上的中间节点,这里简单路径p=<![]() >上的中间节点指的是路径p上除和之外的任意结点。
>上的中间节点指的是路径p上除和之外的任意结点。
假定图G的所有节点V={1,2,...,n},考虑其中的子集{1,2,...,k}。对于任意的结点i,j∈V,考虑从i到j的所有中间节点均取自集合{1,2,...,k}的路径。并设p为其中的最短路径,分两种情况讨论:
a:如果结点k不是p上的中间节点,则路径p上的所有中间节点都属于集合{1,2,...,k-1}。因此,从i到j的中间节点均取自集合{1,2,...,k}的一条最短路径,同样也是从i到j的中间节点均取自集合{1,2,...,k-1}的一条最短路径。
b:如果结点k是路径p上的中间节点,则p可以分解为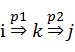 ,所以,p1上的所有中间节点都属于集合{1,2,...,k-1},同理p2也是。
,所以,p1上的所有中间节点都属于集合{1,2,...,k-1},同理p2也是。
根据上面的观察,设![]() 为从i到j的所有中间节点全部取自集合{1,2,...,k}的一条最短路径的权重。当k=0时,i到j的路径没有中间节点,这样的路径最多只有一条边,所以有
为从i到j的所有中间节点全部取自集合{1,2,...,k}的一条最短路径的权重。当k=0时,i到j的路径没有中间节点,这样的路径最多只有一条边,所以有![]() = 。根据上面的讨论,可以有:
= 。根据上面的讨论,可以有:
因为对于所有的路径,所有的中间节点都属于集合{1,2,...,n},矩阵![]() =
=![]() 给出的就是最终的矩阵:
给出的就是最终的矩阵: ![]() =δ(i, j)。算法如下,该算法的运行时间为O(
=δ(i, j)。算法如下,该算法的运行时间为O(![]() ):
):
另外,可以在计算![]() 的同时计算前驱矩阵,具体来说,需要计算一个矩阵序列:,这里
的同时计算前驱矩阵,具体来说,需要计算一个矩阵序列:,这里![]() =,并且定义
=,并且定义![]() 为从i到j的一条所有中间节点都取自集合{1,2,...,k}的最短路径上,j的前驱结点。
为从i到j的一条所有中间节点都取自集合{1,2,...,k}的最短路径上,j的前驱结点。
所以,可以给出的一个递归公式,当k=0时,从i到j的一条最短路径上没有中间节点,所以:
如果k>1,则有:
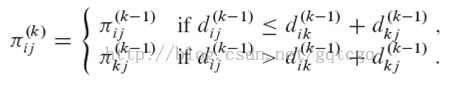 ,这样,就可以在计算的同时,计算前驱矩阵
,这样,就可以在计算的同时,计算前驱矩阵![]() 了,下面是一个运算过程:
了,下面是一个运算过程:
给定有向图G=(V, E),结点集合V={1,2,..., n},希望判断对于所有的i和j,图G中是否包含一条从节点i到j的路径,这称为图G的传递闭包问题。
一种计算图G的传递闭包的办法是给E中的每条边赋予权重1,然后运行Floyd-Warshall算法,如果存在一条从i到j的路径,则有![]() < n;否则,
< n;否则,![]() 。这种算法的时间复杂度为O(
。这种算法的时间复杂度为O(![]() )。
)。
可以有另外一种算法,该算法使用逻辑或操作和逻辑与操作替换Floyd-Warshall算法中的算术操作min和+。对于i,j,k=1,2,...,n,定义:如果图G中存在一条从节点i到结点j的所有中间节点都取自集合{1,2,...,k}的路径,则 ![]() = 1,否则, = 0。所以,当k=0时,有:
= 1,否则, = 0。所以,当k=0时,有:
,对于k>=1,有:
= ,所以算法如下:
该算法从结构上类似于Floyd-Warshall算法,运行时间为O(![]() ),但是逻辑运算通常要比算术运算要快,而且TRANSITIVE-CLOSURE所需要的空间更少。
),但是逻辑运算通常要比算术运算要快,而且TRANSITIVE-CLOSURE所需要的空间更少。
三:用于稀疏图的johnson算法
johnson算法可以在O()时间内找到所有节点对之间的最短路径。对于稀疏图来说,算法在渐近意义上要好于矩阵的重复平方法或Floyd-Warshall算法。算法要么返回一个包含所有节点对的最短路径权重的矩阵,要么报告输人图中存在一个负权值的回路。算法需要使用Dijkstra算法和Bellman-Ford算法作为其子程序。
Johnson算法使用的技术称为重新赋予权重。如果图G=(V, E)中所有的边权重w皆为非负值,则可以采用对每个节点运行Dijkstra算法找到所有节点对的最短路径,如果该图包含权重为负值的边,但没有权重为负值的环路,则只要计算出一组新的非负权重值,然后使用同样的方法即可。新赋予的权重w’必须满足下面的性质:
a:多于所有顶点对u、v∈V,一条路径p是利用加权函数w时从u到v的一条最短路径,当且仅当p也是利用加权函数w’时从u到v的一条最短路径。
b:对于所有的边(u, v),新的权重w’(u, v)是非负值。
给定带权重的有向图G=(V, E),其权重函数为w,设h: v->R为任意函数,该函数将节点映射到实数上。对于每条边(u,v),定义w’(u,v)= w(u, v) + h(u) – h(v)。设p = <>为从节点![]() 到节点
到节点![]() 的任意一条路径,那么p是在使用权重函数w时从节点到节点的一条最短路径,当且仅当p是在使用权重函数w’时从节点到节点的一条最短路径。即w(p) = δ(
的任意一条路径,那么p是在使用权重函数w时从节点到节点的一条最短路径,当且仅当p是在使用权重函数w’时从节点到节点的一条最短路径。即w(p) = δ(![]() )当且仅当w’(p) =δ'(
)当且仅当w’(p) =δ'(![]() )。而且,图G在使用权重函数w时不包含负值环路,当且仅当G在使用权重函数w’时不包含负值环路。
)。而且,图G在使用权重函数w时不包含负值环路,当且仅当G在使用权重函数w’时不包含负值环路。
下一个目标是确保第二个属性成立,也就是所有边(u, v),w’(u,v)>=0。如果给定图G=(V, E),制作一幅新图G’ = (V’, E’)。其中V’ = V∪{s},s是一个新节点。E’ = E∪ {(s,v): v∈V},并且,对于所有节点v∈V, w(s, v) = 0。所以G’不包含权重为负值的环路当且仅当图G不包含权重为负值的环路。现在定义函数h,对于所有节点v∈V’,h(v) =(s)。所以w’(u, v) = w(u, v)+ h(u) – h(v)。根据三角不等式定理,可以得到w’(u, v)>=0。
Johnson算法执行过程中需要使用Bellman-ford算法和Dijkstra算法。该算法假定所有的边都保存在邻接链表里,返回一个|V|*|V|的矩阵D =![]() ,其中
,其中![]() =δ(i, j)。
=δ(i, j)。
如果使用斐波那契堆来实现Dijkstra算法,则Johnson算法的运行时间为O(![]() ),使用更简单的二叉堆实现,则时间为O(VE lg V),在稀疏图的情况下,仍然比Floyd-warshall算法快。
),使用更简单的二叉堆实现,则时间为O(VE lg V),在稀疏图的情况下,仍然比Floyd-warshall算法快。