白话空间统计之五:空间关系的概念化(下)
空间关系的概念化,在ArcGIS中,一共是有7种。前面我们说了反距离、距离范围、无差别区域和面邻接四种,后面还有三种今天一并说完。
后面的几种,其实也都是在前面的那些“简单粗暴”的模型中发展而来的,正所谓“大道至简”一点也没错。
五、K 最近相邻要素
所谓的K最近相邻,就是指在一定的范围内,都算相邻的要素,这个概念是“距离范围”模型改良之后生成的。距离范围是以一定距离为阈值,而这个模型是以要素的个数为阈值的。
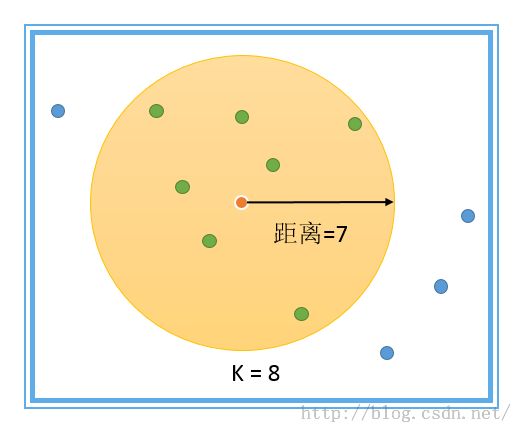
比如,你选定了K=8,那么这个要素周边的8个要素,都将作为你的相邻要素参与计算,这是一种搜索距离可变的模型,如下:
在中心点附近,选择你最近的k个点,组成你的邻近要素集,这个距离是可变的,如果要素分布的比较离散,那么搜索的距离就会变大,如下:
这种模型的优点,在于它可以确保每个目标要素都能找到相邻的要素,特别是在一些在研究区域内,要素分布非常不均匀的,密度差别非常大的情况下,也能保证有相邻要素的存在。
K邻近模型在一些数学研究中有很广泛的应用,例如在素数的研究中,因为素数是随机在数轴上出现的,所以你无法圈定的一个固定的范围,来决定你的相邻要素(素数有孪生素数问题,也就是相邻可能只有1:比如3和5,5和7,17和19这种,当然,两个素数之间距离也可能无穷大),所以如果要获取一些邻近要素的时候,就只能去选择这一类的模型了。
六、Delaunay 三角测量(自然相邻要素)
Delaunay三角算法是俄罗斯著名数学家鲍里斯 尼古拉耶维奇 德劳内(Boris Nikolaevich Delaunay 1890-1980)在1934年最先提出来的,用于对点集进行三角网划分的方法。
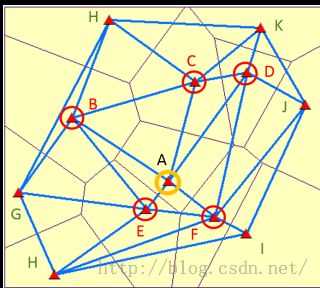
而在空间关系概念化里面,利用这个方法来确定相邻要素,确实是一种很有意思的方法。具体的做法,是首先利用点(如果是面要素的话,就利用面的质心点)来创建一个Voronoi 三角形,使得每个点(质心)都是三角形结点。
如下图:
A点与B、C、D、E、F,都有共同的三角网,那么BCDEF五个点,就被设为A点的相邻要素。
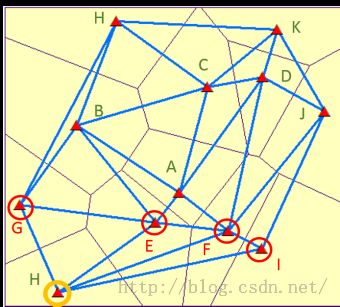
同样的如果要计算H点的相邻要素,就变成了E、F、I、G了,如下:
使用Delaunay 三角测量模型,和K邻近一样,可以确保你要计算的每个要素至少具有一个相邻要素,即使你的数据包含有岛状要素或者带有空洞的要素。另外,这个模型和K邻近一样,不会在乎你的要素分布是不是均匀。
需要注意的是,如果你的数据出现了重合要素的时候,不要使用Delaunay 三角测量选项。
七、空间时间窗
这是ArcGIS里面七种空间关系概念化的最后一种,是一种时空组合的空间关系概念模型。用这个模型的时候,需要你的数据同时具有空间属性和时间属性。
这个模型会同时兼顾时间间隔和空间间隔,首先要确定时间关系,在ArcGIS里面,时间间隔有月日时三种模式,间隔值一般是整数。比如我们选择以小时为间隔单位,窗口大小为3,那么上下限为三个小时之内的数据,都被视为相邻要素。当然,还要兼顾空间的关系,所以选择这个选项的时候,往往会同时考虑空间(在指定范围内)和时间(指定时间区间)两个因素。
此类模型,在对时间间隔要有要求的分析中,很实用。比如犯罪分析,同一个犯人,是不可能在同一时间在不同地点犯案的。
ArcGIS 在10.3中,推出了一个新的“时空分析”工具箱,用的就是这种模型。
到此,空间关系概念化的七种模型就全部写完了,这些模型在什么时候用,特别是在ArcGIS软件中如何用,那么老规矩,先挖坑,以后慢慢填。